Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
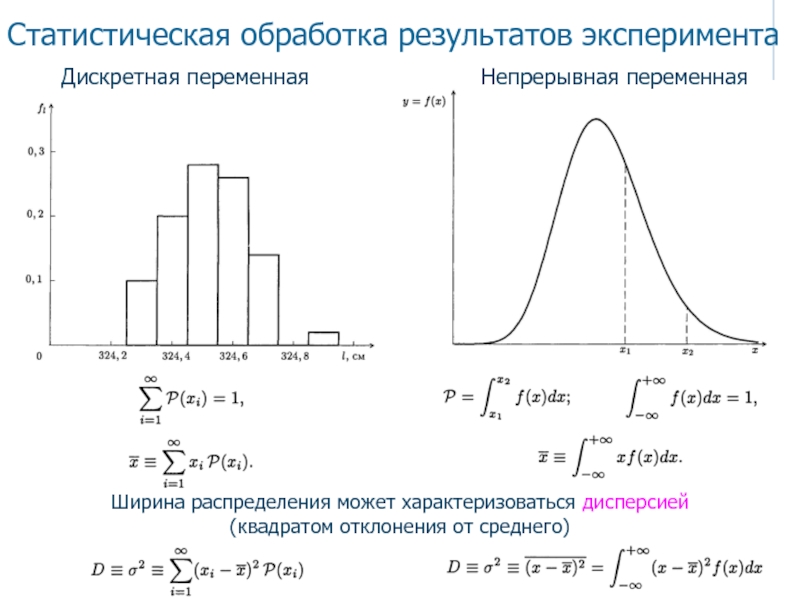
Статистическая обработка результатов эксперимента
Содержание
- 1. Статистическая обработка результатов эксперимента
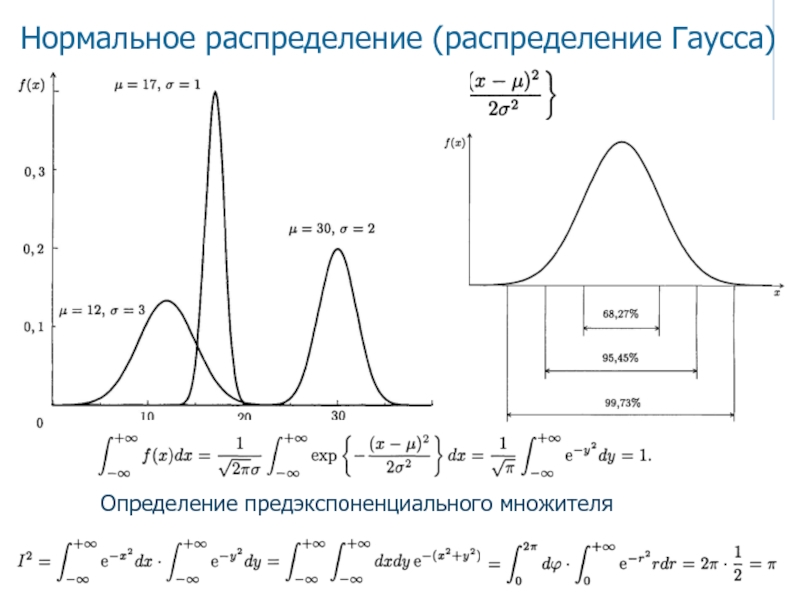
- 2. Определение предэкспоненциального множителяНормальное распределение (распределение Гаусса)
- 3. Другие виды распределений:- Биноминальное (дискретное)- Стьюдента- Пуассона- Лоренца- Гамма-распределение- распределение c2Биноминальное распределениеd - абсолютная погрешность
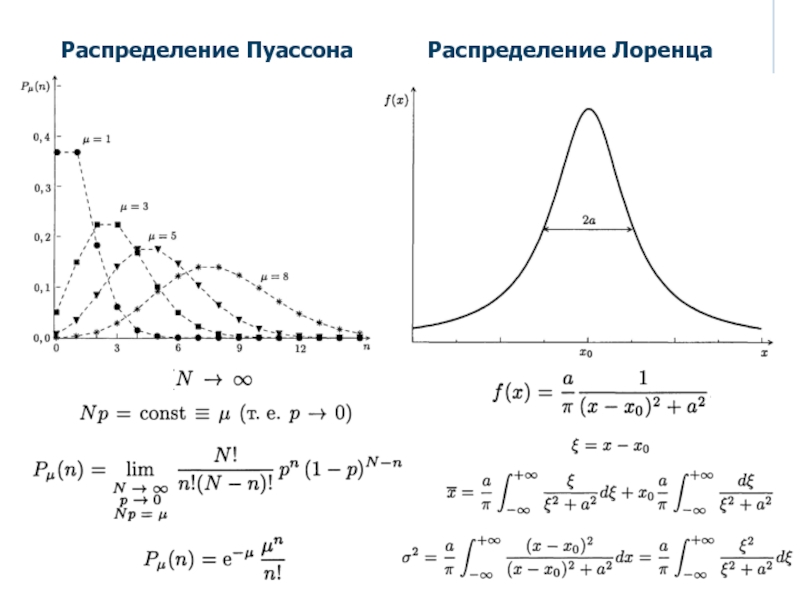
- 4. Распределение ПуассонаРаспределение Лоренца
- 5. Гамма-распределениеСвойства Г-функцииРаспределение вероятностей
- 6. Распределение c2Распределение СтьюдентаПри малом n
- 7. Соотношения между различными распределениями
- 8. Слайд 8
- 9. Статистическая обработка результатов эксперимента Если в результате
- 10. Слайд 10
- 11. Распространение ошибок
- 12. Скачать презентанцию
Определение предэкспоненциального множителяНормальное распределение (распределение Гаусса)
Слайды и текст этой презентации
Слайд 1Статистическая обработка результатов эксперимента
Дискретная переменная
Непрерывная переменная
Ширина распределения может характеризоваться
дисперсией
(квадратом отклонения от среднего)
Слайд 3Другие виды распределений:
- Биноминальное (дискретное)
- Стьюдента
- Пуассона
- Лоренца
- Гамма-распределение
- распределение
c2
Биноминальное распределение
d - абсолютная погрешность
Слайд 9Статистическая обработка результатов эксперимента
Если в результате измерения n раз
некоторой физической величины x получен ряд значений x1, x2, ...,
xn, то в качестве значения, наиболее близкого к истинному, принимается среднее арифметическоеСлучайную ошибку измерений оценивают по среднеквадратичному отклонению от среднего значения измеряемой величины x.
Истинное значение измеренной величины x лежит в интервале от до
, где x называется доверительным интервалом. Вероятность этого события (доверительная вероятность) составляет P.
Доверительный интервал рассчитывается по формуле
где tP,n-1 - коэффициент Стьюдента, зависящий от доверительной вероятности P и числа измерений n.
Таким образом, окончательная форма записи результата имеет вид