Статистическая проверка гипотез

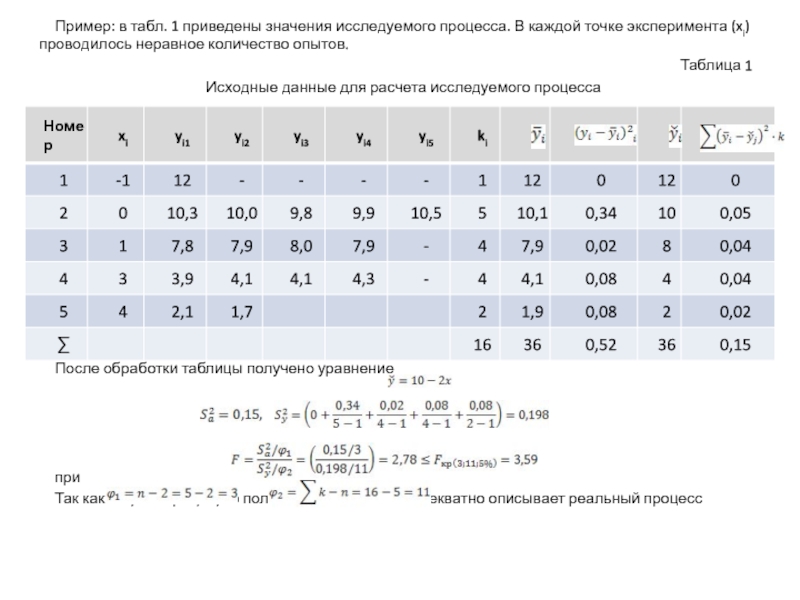
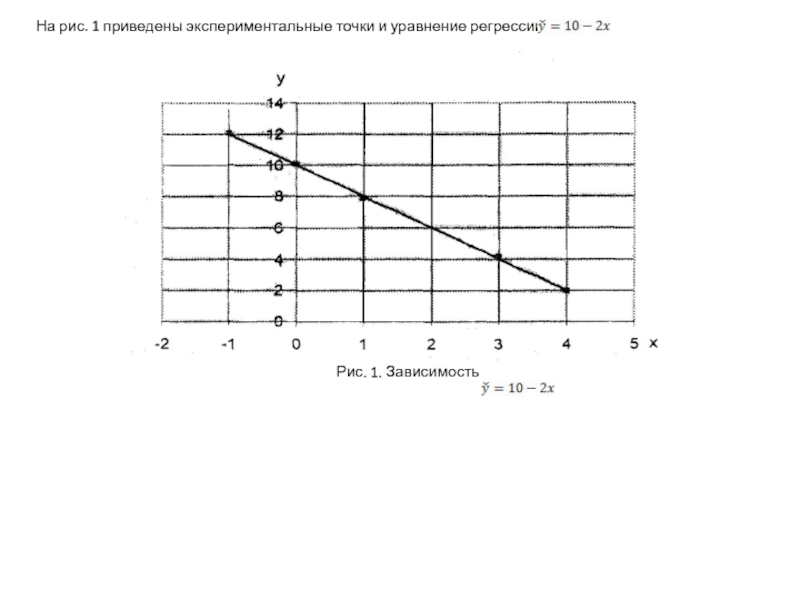
показывает, во сколько раз уравнение регрессии предсказывает результаты опыта лучше,

чем среднее по опытам.
Если число опытов в каждой точке равно одному, а общее число точек равно (n), то





где - число степеней свободы дисперсии эксперимента,
- число степеней свободы дисперсии адекватности (остаточной дисперсии)
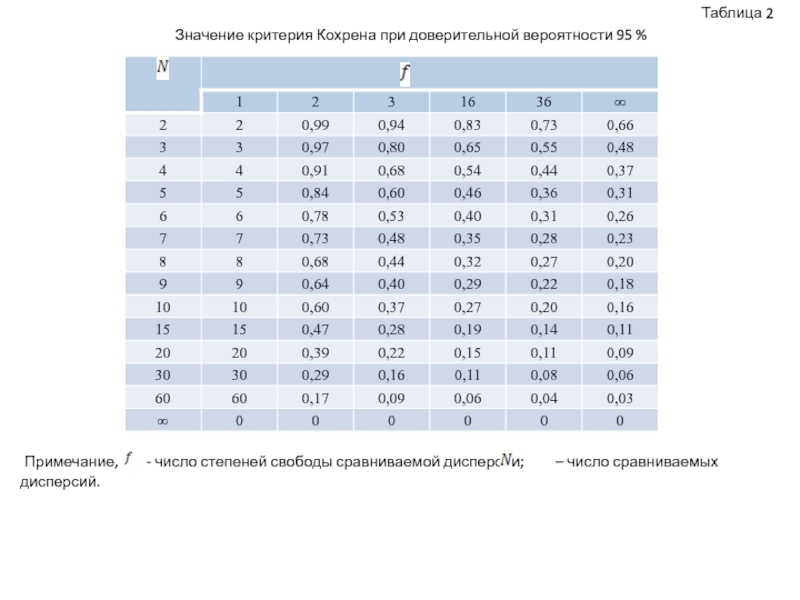
- табличное (критическое) значение критерия Фишера при уровне значимости «р».
Если число опытов в каждой точке разное и равно ki , число точек равно (n), а общее число экспериментов во

всех опытах , то расчетное значение критерия Фишера и условие адекватности определяется из формулы



Где - дисперсия эксперимента;

ЛЕКЦИЯ 23 СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ

точке эксперимента (xi) проводилось неравное количество опытов.
Таблица 1
Исходные данные для

расчета исследуемого процесса












После обработки таблицы получено уравнение




при
Так как F=2,78

эксперимента в другой промежуток времени. Расчетное значение критерия Кохрена равно

отношению максимальной дисперсии в одной точке к сумме дисперсий всего эксперимента. Если расчетное значение критерия при заданном уровне значимости должно быть меньше критического (Gтабл), то дисперсии однородны. В противном случае опыты поставлены некорректно, т.е. имеется неслучайный фактор, влияющий на результат.



где - число степеней свободы;
ki – число опытов в каждой точке
- max из дисперсий в одной из точек эксперимента
- число точек эксперимента.
Максимальная дисперсия в одной из точек (в данном эксперименте она во второй точке) находится из формулы:


Пример: Проверить однородность дисперсии эксперимента, результаты которого приведены в таблице 1.




Вывод: дисперсии однородны.

Таким образом, полученная модель может быть использована для прогнозирования ещё не известных результатов процесса, который она описывает.

1. Зависимость

- число степеней свободы сравниваемой дисперсии;

– число сравниваемых дисперсий.