Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
СТРУКТУРЫ ДАННЫХ Лектор Спиричева Наталия Рахматулловна Ст. преподаватель каф
Содержание
- 1. СТРУКТУРЫ ДАННЫХ Лектор Спиричева Наталия Рахматулловна Ст. преподаватель каф
- 2. Структуры данных Структуры данныхСоставитель курса лекций:Спиричева Наталия Рахматулловна, ст. преподаватель каф. Информационных технологий
- 3. Спиричева Н.Р. ГРАФЫ
- 4. Структуры данных Структуры данных и алгоритмы Целью лекции является
- 5. Структуры данных Структуры данных и алгоритмыОсновные темы лекции:Понятие древовидных структурДеревьяГрафыАлгоритмы поиска путей в графах
- 6. Спиричева Н.Р. Первая работа
- 7. Спиричева Н.Р. Несколько модифицируем
- 8. Спиричева Н.Р. Предположим, что
- 9. Спиричева Н.Р. Схема такого
- 10. Структуры данных Введение Сетевые структуры – весьма общий и гибкий класс связных списков.
- 11. Структуры данных ВведениеДерево - конечное множество, состоящее из
- 12. Структуры данных Введение Определим дерево как конечное множество Т,
- 13. Структуры данных Из определения следует:Каждый узел дерева является
- 14. Структуры данных Введение Обычно дерево представляется в машинной памяти
- 15. Структуры данных Введение Сетевые структуры – весьма общий и гибкий класс связных списков.
- 16. Спиричева Н.Р. Дерево
- 17. Спиричева Н.Р. Свойства деревьев1.
- 18. Спиричева Н.Р. Рассмотрим произвольное
- 19. Структуры данных Дерево – структура данных, представляющая собой
- 20. Структуры данных Бинарное дерево Бинарное дерево - конечное множество
- 21. Структуры данных Бинарное дерево В алгоритмах работы с древовидными
- 22. Структуры данных Бинарное деревоПрямой порядок обхода:Попасть в кореньПройти
- 23. Структуры данных Бинарное дерево“Прошитые” деревья В “прошитых” деревьях концевые
- 24. Структуры данных ЛЕС Лес – это
- 25. Структуры данных ГрафыГраф - некоторое множество точек (называемых
- 26. Структуры данных ГрафыГраф - некоторое множество точек (называемых
- 27. Спиричева Н.Р. Важным при
- 28. Спиричева Н.Р. Для многих
- 29. Структуры данных Графы Каждая пара вершин
- 30. Структуры данных Графы Пусть V и
- 31. Структуры данных ГрафыГраф называется связным, если имеется путь
- 32. Структуры данных Степень входа вершины – количество входящих
- 33. Структуры данных Графы
- 34. Структуры данных ГрафыЗадание графа: Класс матриц инциденции. Если граф
- 35. Структуры данных Графы
- 36. Структуры данных Графы Класс матриц смежности. Матрица смежности S=[sij]nxm
- 37. Структуры данных Графы
- 38. Спиричева Н.Р. РаскраскиВ теории
- 39. Спиричева Н.Р. Каждый многоугольный
- 40. Спиричева Н.Р. Когда говорят
- 41. Спиричева Н.Р. В теории
- 42. Спиричева Н.Р. Граф-цикл может
- 43. Спиричева Н.Р. В теории
- 44. Структуры данных Алгоритмы поиска путей в графе Путь
- 45. Структуры данных Волновой алгоритмКаждой вершине i приписывается два
- 46. Структуры данных Под корректностью алгоритма здесь понимается, что:
- 47. Структуры данных Алгоритмы поиска путей в графе Путь
- 48. Структуры данных Алгоритмы поиска путей в графе Алгоритм,
- 49. Структуры данных Алгоритмы поиска путей в графе Алгоритм
- 50. Структуры данных Алгоритмы поиска путей в графе Алгоритм
- 51. Структуры данных Алгоритмы поиска путей в графе Алгоритм
- 52. Структуры данных Алгоритмы поиска путей в графе Алгоритм
- 53. Структуры данных Алгоритмы поиска путей в графе Алгоритм
- 54. Структуры данных Алгоритмы поиска путей в графе Алгоритм
- 55. Структуры данных Алгоритмы поиска путей в графе Алгоритм
- 56. Структуры данных Алгоритмы поиска путей в графе Алгоритм
- 57. Структуры данных Алгоритмы поиска путей в графе Алгоритм
- 58. Структуры данных Алгоритмы поиска путей в графе Алгоритм
- 59. Структуры данных Алгоритмы поиска путей в графе Алгоритм
- 60. Структуры данных Алгоритмы поиска путей в графе Алгоритм
- 61. Структуры данных Алгоритмы поиска путей в графе Путь
- 62. Структуры данных Алгоритмы поиска путей в графе Нахождение
- 63. Структуры данных Алгоритмы поиска путей в графе Алгоритм:1.
- 64. Структуры данных 1.Какими структурами данных можно представить в
- 65. Спасибо за внимание!Структуры данных
- 66. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Структуры данных
Структуры данных
Составитель курса лекций:
Спиричева Наталия Рахматулловна,
ст. преподаватель каф.
Информационных технологий
Слайд 4Структуры данных
Структуры данных и алгоритмы
Целью лекции является приобретение студентами следующих
компетенций:
знать методы представления древовидных структур в памяти ЭВМ
знать и уметь
применять алгоритмы поиска путей в графахСлайд 5Структуры данных
Структуры данных и алгоритмы
Основные темы лекции:
Понятие древовидных структур
Деревья
Графы
Алгоритмы поиска
путей в графах
Слайд 6 Спиричева Н.Р.
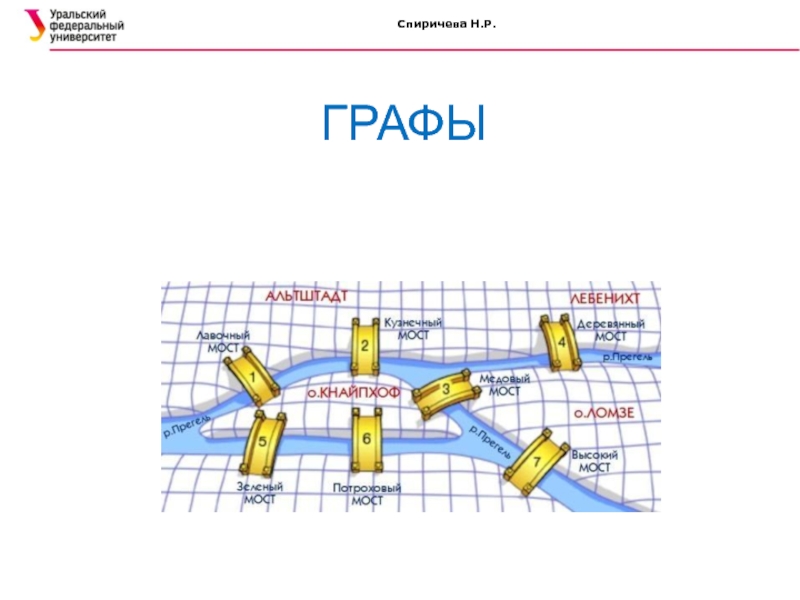
Первая работа по теории графов,
принадлежит известному швейцарскому математику Л. Эйлеру. В 1736 г. Эйлер
решил задачу о Кенигсбергских мостах. Задача состояла в следующем: «Найти маршрут прохождения всех четырех участков суши, который бы начинался на любом из них, кончался на этом же участке и ровно один раз проходил по каждому из них».Слайд 7 Спиричева Н.Р.
Несколько модифицируем задачу. Каждую из
рассматриваемых местностей, разделенных рекой, обозначим точкой, а соединяющие их мосты
– отрезком линии (не обязательно прямой). Тогда вместо плана будем работать просто с некой фигурой, составленной из отрезков кривых и прямых. Такие фигуры в современной математике называются графами, отрезки – ребрами, а точки, которые соединяют ребра – вершинами. Тогда исходная задача эквивалентна следующей: можно ли начертить данный граф, не отрывая карандаша от бумаги, то есть таким образом, чтобы каждое его ребро пройти ровно один раз. Такие графы, которые можно начертить, не отрывая карандаша от бумаги, называются уникурсальными (от латинского unus cursus – один путь), или эйлеровыми. Итак, задача ставится таким образом: при каких условиях граф уникурсален? Ясно, что уникурсальный граф не перестанет быть уникурсальным, если изменить длину или форму его ребер, а также изменить расположение вершин – лишь бы не менялось соединение вершин ребрами (в том смысле, что если две вершины соединены, они должны оставаться соединенными, а если разъединены – то разъединенными).Слайд 8 Спиричева Н.Р.
Предположим, что футбольная команда вашей
школы участвует в соревнованиях и играет с командами других школ.
Пусть общее число команд равно шести. Вашу команду обозначим буквой А, а другие команды-буквами В, С, D,E и F. Через несколько недель после начала соревнований окажется, что не которые из команд уже сыграли друг с другом,например:A с C,D,F
B с C,E,F
C c A,B
D c A,E,F
E c B,D,F
F c A,B,D,E
Это можно изобразить при помощи такой геометрической схемы. Каждую команду представим точкой или маленьким кружочком и соединим отрезком те пары точек, которые соответствуют командам, уже игравшим друг с другом.
Слайд 9 Спиричева Н.Р.
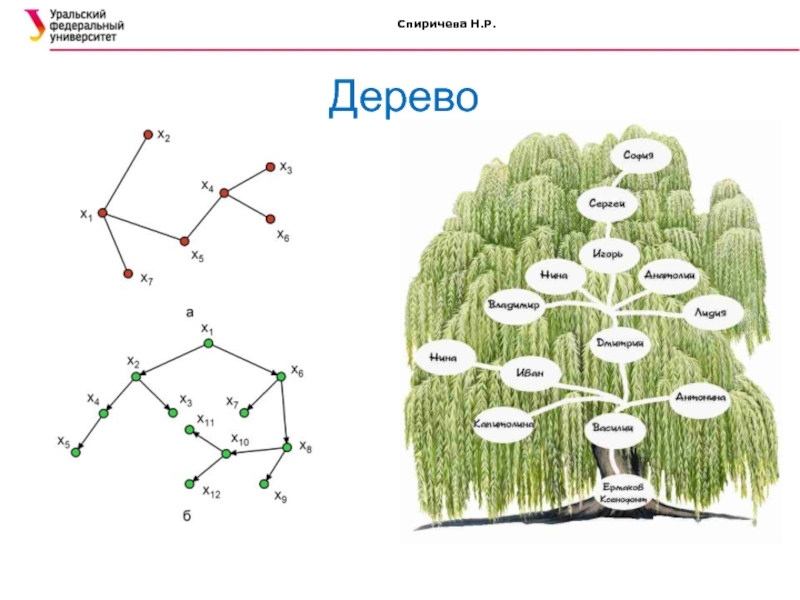
Схема такого вида называется графом.
Она состоит из нескольких точек А, В, С, D. Е,
F, называемых вершинами, и нескольких соединяющих эти точки отрезков, таких, как АС или ЕВ, называемых ребрами графа. Каждую совокупность игр любого турнира можно представить соответствующим графом. Наоборот, если задан некоторый граф, т. е. фигура, состоящая из точек-вершин, соединенных прямолинейными отрезками-ребрами, то его можно рассматривать как схему такого состязания.Слайд 11Структуры данных
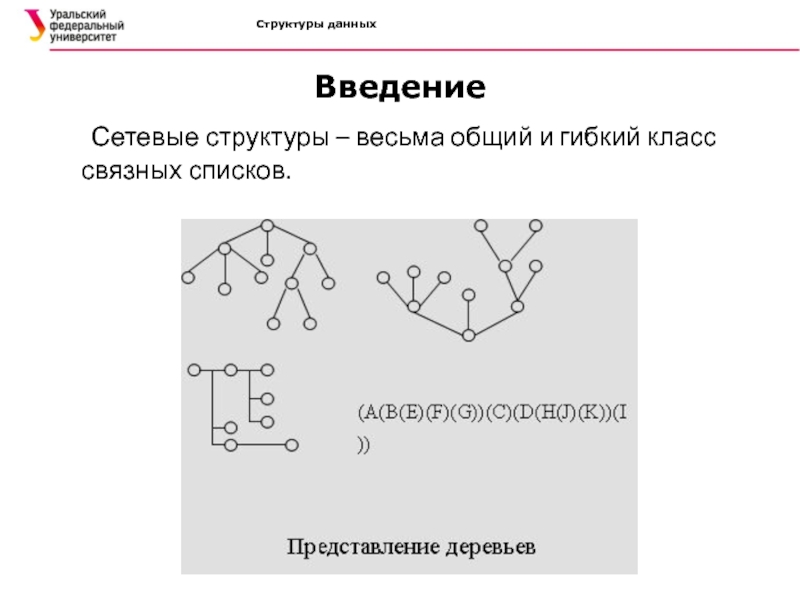
Введение
Дерево - конечное множество, состоящее из одного или более
элементов, называемых узлами.
Корень - узел, не имеющий исходного. Все узлы,
кроме корня, имеют только один исходный. Есть деревья, состоящие из одного корня. Каждый узел может иметь несколько порождённых. Слайд 12Структуры данных
Введение
Определим дерево как конечное множество Т, состоящее из одного
или более узлов, таких, что
а) имеется один специально обозначенный
узел, называемый корнем данного дерева,б) остальные узлы (исключая корень) содержатся в m0 попарно непересекающихся множествах Т1, …, Тm, каждое из которых в свою очередь является деревом. Деревья Т1, …, Тm называются поддеревьями данного корня.
Слайд 13Структуры данных
Из определения следует:
Каждый узел дерева является корнем некоторого поддерева,
которое содержится в этом дереве.
Число поддеревьев данного узла называется
степенью этого узла. Узел с нулевой степенью называется концевым узлом;
Неконцевые узлы часто называют узлами разветвления.
Уровень узла по отношению к дереву Т определяется следующим образом: говорят, что корень имеет уровень 1, а другие узлы имеют уровень на 1 выше их уровня относительно содержащего их поддерева Тj этого корня.
Слайд 14Структуры данных
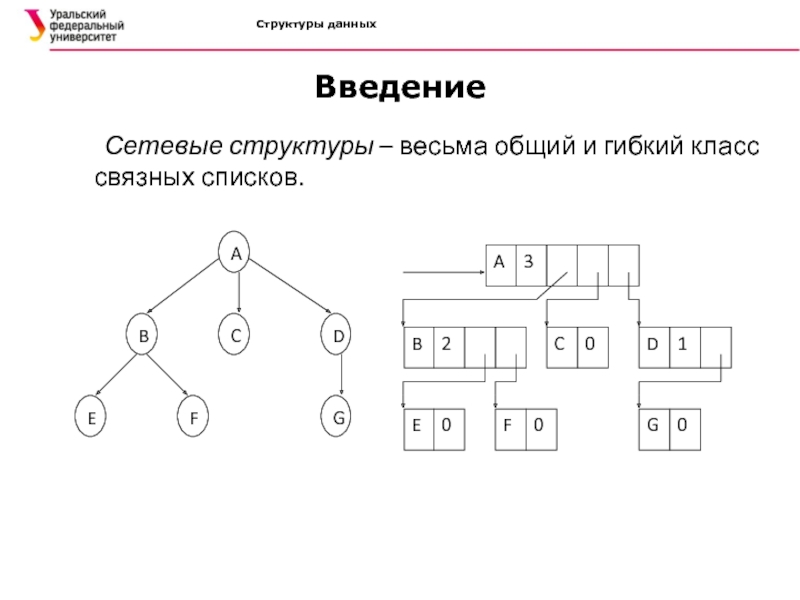
Введение
Обычно дерево представляется в машинной памяти в форме многосвязного
списка, в котором каждый указатель соответствует дуге. Это представление называется
естественным представлением дерева. Существуют несколько разновидностей такого представления. В одной из наиболее общих разновидностей каждому узлу дерева ставится в соответствие элемент многосвязного списка, причем в каждом элементе отводятся следующие поля: поле данных, поле степени исхода (т.е. числа сыновей) и поля указателей, число которых равно степени исхода.Слайд 17 Спиричева Н.Р.
Свойства деревьев
1. Любая пара вершин
соединена единственным маршрутом.
2. Количество ребер меньше на одну чем вершин.
3.
Удаление хотя бы одного ребра не нарушает его структуру.4. если в дерево добавить хотя бы одно ребро то появиться цикл.
Деревья - очень удобный инструмент представления информации самого разного вида. Они отличаются от простых графов тем, что при обходе дерева невозможны циклы. Это делает графы очень удобной формой организации данных для различных алгоритмов. Таким образом, понятия дерева активно используется в информатике и программировании.
Слайд 18 Спиричева Н.Р.
Рассмотрим произвольное дерево.Для того чтобы
построить дерево, выберем какую нибудь вершину А0 Из А0 проведем
ребра в соседние вершины А1, А2, ..., из них проведем ребра к их соседям А11, А12, ..., А21, А22, ... и т. д., как показано на рис. 34. Первоначально выбранная вершина А0 называется корнем дерева; каждая вершина дерева может служить его корнем.Слайд 19Структуры данных
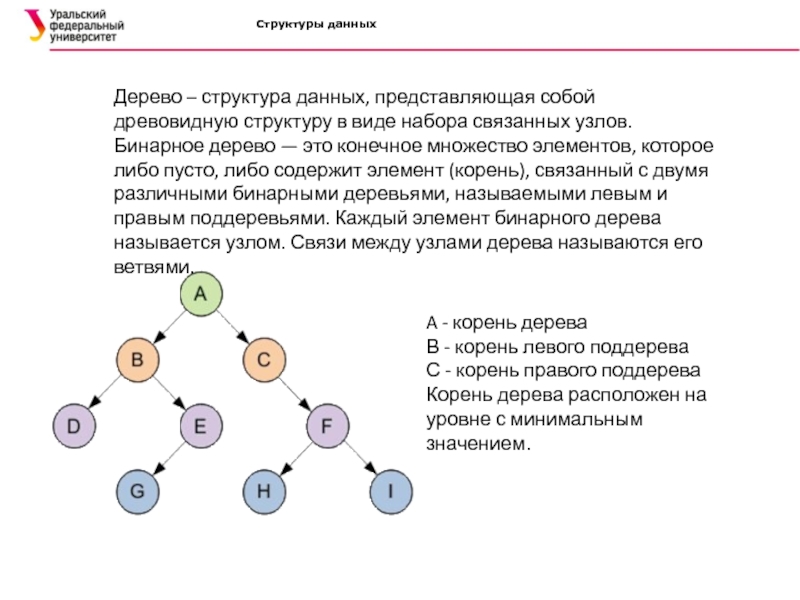
Дерево – структура данных, представляющая собой древовидную структуру в
виде набора связанных узлов.
Бинарное дерево — это конечное множество элементов,
которое либо пусто, либо содержит элемент (корень), связанный с двумя различными бинарными деревьями, называемыми левым и правым поддеревьями. Каждый элемент бинарного дерева называется узлом. Связи между узлами дерева называются его ветвями.A - корень дерева
В - корень левого поддерева
С - корень правого поддерева
Корень дерева расположен на уровне с минимальным значением.
Слайд 20Структуры данных
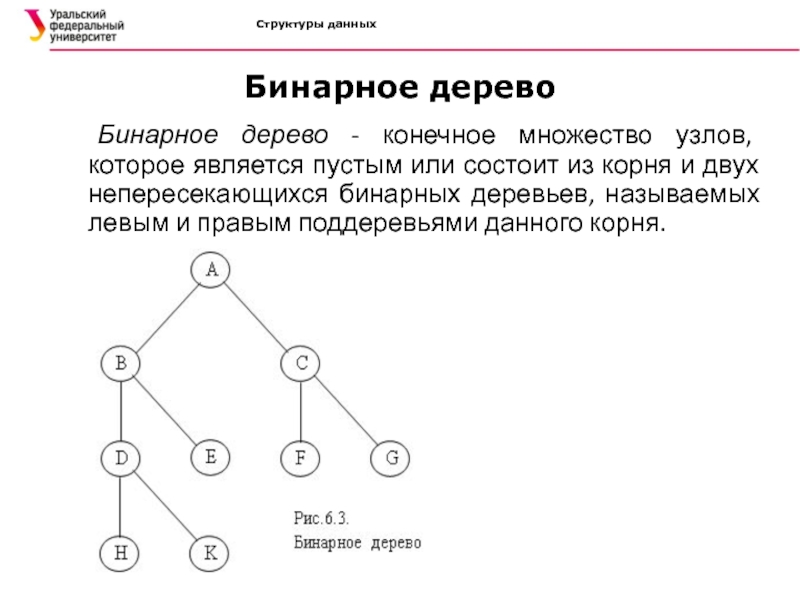
Бинарное дерево
Бинарное дерево - конечное множество узлов, которое является
пустым или состоит из корня и двух непересекающихся бинарных деревьев,
называемых левым и правым поддеревьями данного корня.Слайд 21Структуры данных
Бинарное дерево
В алгоритмах работы с древовидными структурами наиболее часто
встречается понятие обход дерева.
Для обхода бинарных деревьев можно применить
один из
трех принципиально разных способов:в прямом порядке
в центрированном порядке
в обратном порядке
Слайд 22Структуры данных
Бинарное дерево
Прямой порядок обхода:
Попасть в корень
Пройти левое поддерево
Пройти правое
поддерево
Центрированный порядок обхода:
Пройти левое поддерево
Попасть в корень
Пройти правое поддерево
Обратный порядок
обхода:Пройти левое поддерево
Пройти правое поддерево
Попасть в корень
Слайд 23Структуры данных
Бинарное дерево
“Прошитые” деревья
В “прошитых” деревьях концевые связи-указатели используются для
связи с родителями, такие связи назвали нитями.
Отличие нормальных связей
от нитей: в каждом узле хранят две однобитовые переменные LTag и RTag. Эти переменные равны нулю, если соответствующие связи указывают на поддеревья, и единице, если связи являются нитями. Левая нить каждого узла указывает на узел, являющийся предшественником данного при центрированном обходе, правая - на узел, являющийся последователем данного узла.
Слайд 24Структуры данных
ЛЕС
Лес – это множество (обычно упорядоченное),
состоящее из некоторого (быть может равного нулю) числа непересекающихся деревьев.
Слайд 25Структуры данных
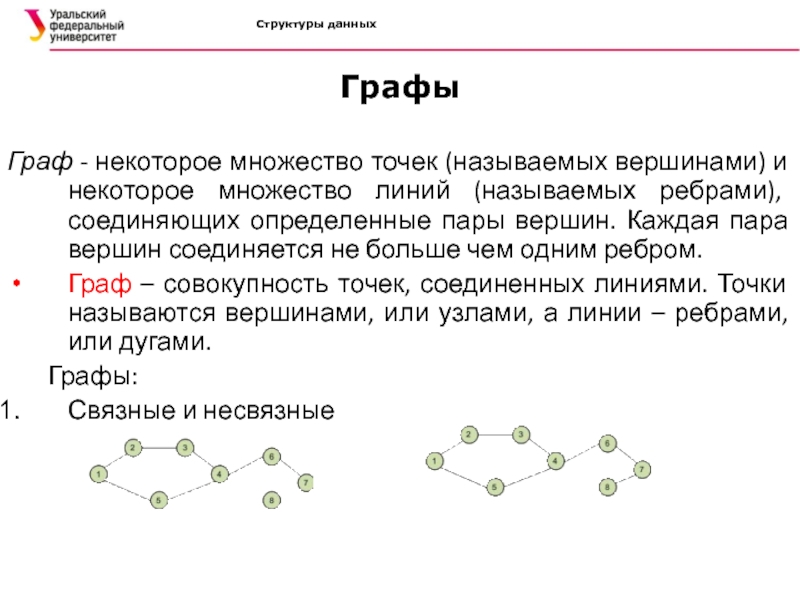
Графы
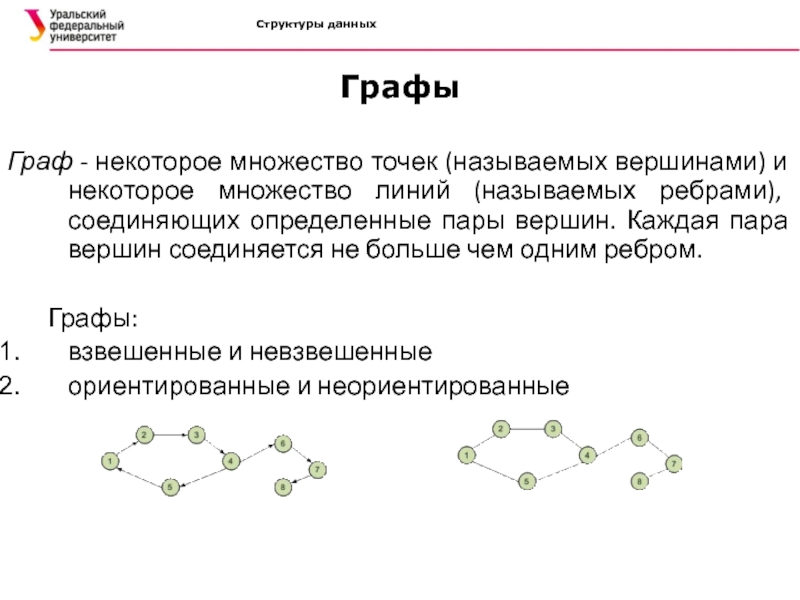
Граф - некоторое множество точек (называемых вершинами) и некоторое
множество линий (называемых ребрами), соединяющих определенные пары вершин. Каждая пара
вершин соединяется не больше чем одним ребром.Граф – совокупность точек, соединенных линиями. Точки называются вершинами, или узлами, а линии – ребрами, или дугами.
Графы:
Связные и несвязные
Слайд 26Структуры данных
Графы
Граф - некоторое множество точек (называемых вершинами) и некоторое
множество линий (называемых ребрами), соединяющих определенные пары вершин. Каждая пара
вершин соединяется не больше чем одним ребром.Графы:
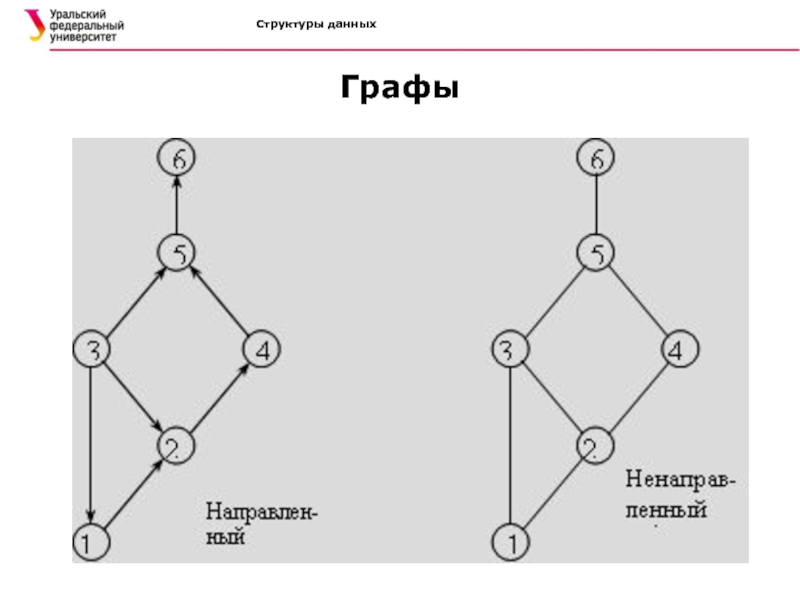
взвешенные и невзвешенные
ориентированные и неориентированные
Слайд 27 Спиричева Н.Р.
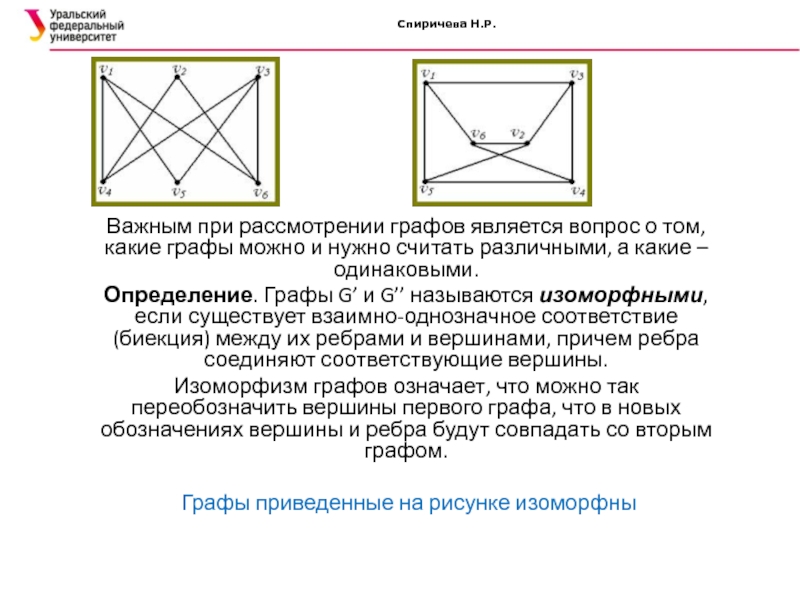
Важным при рассмотрении графов является
вопрос о том, какие графы можно и нужно считать различными,
а какие – одинаковыми.Определение. Графы G’ и G’’ называются изоморфными, если существует взаимно-однозначное соответствие (биекция) между их ребрами и вершинами, причем ребра соединяют соответствующие вершины.
Изоморфизм графов означает, что можно так переобозначить вершины первого графа, что в новых обозначениях вершины и ребра будут совпадать со вторым графом.
Графы приведенные на рисунке изоморфны
Слайд 28 Спиричева Н.Р.
Для многих целей безразлично, как
именно изображен граф, т. е. изоморфные графы, доставляющие одну и
ту же информацию, могут рассматриваться как один граф.(, например, когда граф играет роль своеобразного списка уже проведенных игр). Однако в других случаях существенно то обстоятельство, что граф может быть начерчен некоторым специальным образом.Граф, который можно начертить таким образом, чтобы его ребра пересекались только в вершинах, называется плоским графом. Так, граф G, изображенный на рис. 1, является плоским, потому что существует изоморфный ему граф (рис. 7), все ребра которого пересекаются только в вершинах.
Слайд 29Структуры данных
Графы
Каждая пара вершин в графе соединяется
не больше чем одним ребром. Дуга, соединенная с вершиной, называется
инцидентной этой вершине. Две вершины называются смежными, если существует ребро, соединяющее их. Две дуги называются смежными, если они инцидентны одной и той же вершине.Слайд 30Структуры данных
Графы
Пусть V и V` - вершины
и пусть n0; говорят, что «V0, V1, …, Vn» -
путь длины n от V до V`, если V=V0, вершина Vk смежна с Vk+1 при 0kn, а Vn=V`. Путь прост, если вершины V0, V1, …, Vn-1 все различны между собой, а также различны все вершины V1, V2, …, Vn. Граф называется связным, если имеется путь между каждыми двумя вершинами этого графа. Циклом называется простой путь длины не менее 3 от какой-либо вершины до нее самой. Свободное дерево – это связный граф, не имеющий циклов.Слайд 31Структуры данных
Графы
Граф называется связным, если имеется путь между каждыми двумя
вершинами этого графа.
Циклом называется простой путь длины не менее
3 от какой-либо вершины до нее самой. Свободное дерево – это связный граф, не имеющий циклов.Формально направленный граф определяется как некое множество вершин и множество дуг, причем каждая дуга ведет от некоторой вершины V к некоторой вершине V`. Если e – дуга, идущая от V к V`, то говорят, что V – начальная вершина дуги e, а V` - конечная вершина.
Слайд 32Структуры данных
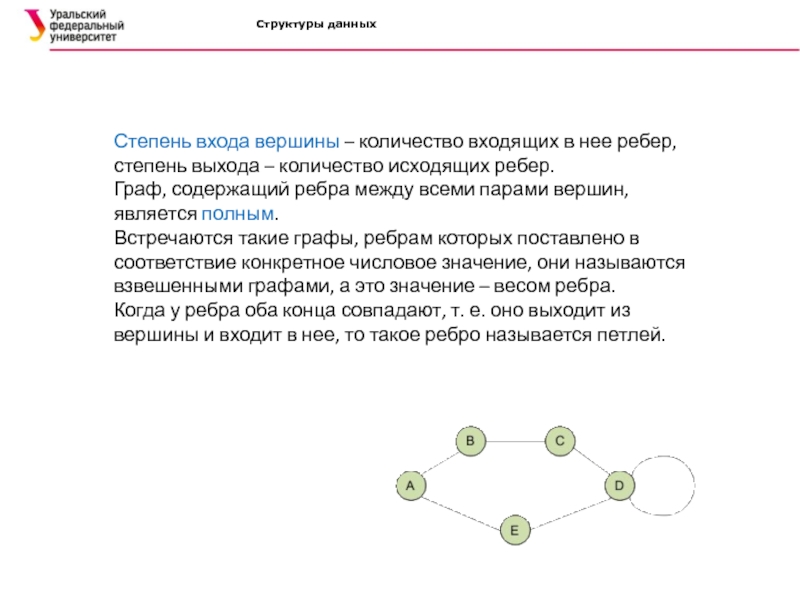
Степень входа вершины – количество входящих в нее ребер,
степень выхода – количество исходящих ребер.
Граф, содержащий ребра между всеми
парами вершин, является полным.Встречаются такие графы, ребрам которых поставлено в соответствие конкретное числовое значение, они называются взвешенными графами, а это значение – весом ребра.
Когда у ребра оба конца совпадают, т. е. оно выходит из вершины и входит в нее, то такое ребро называется петлей.
Слайд 34Структуры данных
Графы
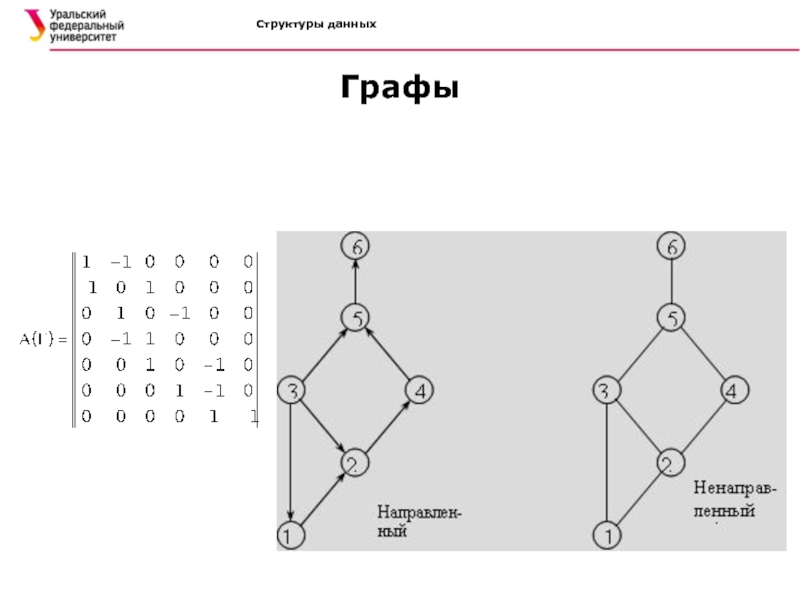
Задание графа:
Класс матриц инциденции. Если граф Г содержит n
вершин и m дуг, то матрица инциденции А(Г)=[aij]mxn определяется так:
Слайд 36Структуры данных
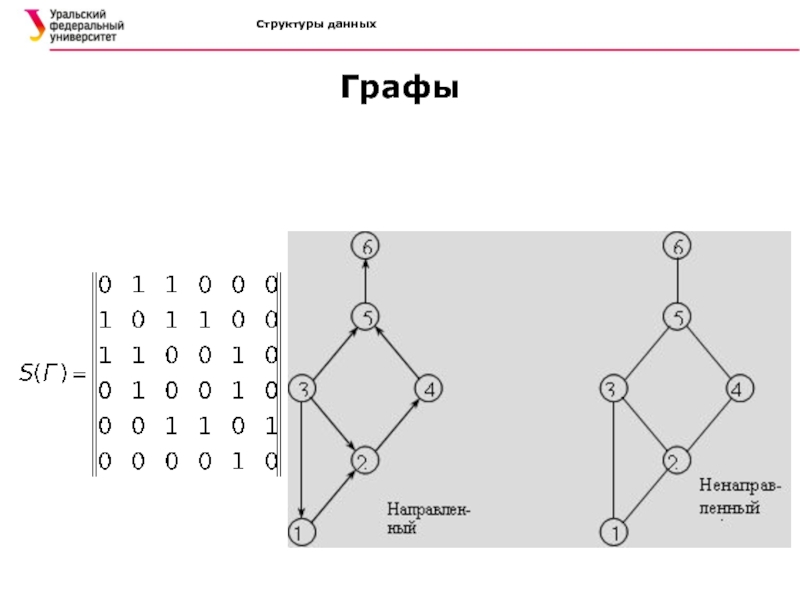
Графы
Класс матриц смежности. Матрица смежности S=[sij]nxm невзвешенного графа определяется
следующим образом:
Во взвешенном графе каждая единица заменяется на вес соответствующего
ребра Слайд 38 Спиричева Н.Р.
Раскраски
В теории графов, раскраска графов
является частным случаем разметки графов. При раскраске элементам графа ставятся
в соответствие метки с учетом определенных ограничений; эти метки традиционно называются “цветами”. В простейшем случае, такой способ окраски вершин графа, при котором любым двум смежным вершинам соответствуют разные цвета, называется окраской вершин. Аналогично, раскраска ребер присваивает цвет каждому ребру так, чтобы любые два смежных ребра имели разные цвета. Наконец, раскраска областей плоского графа назначает цвет каждой области, так, что каждые две области, имеющие общую границу, не могут иметь одинаковый цвет. Раскраска вершин – главная проблема раскраски графов, все остальные задачи в этой области могут быть перенесены на эту модель. Например, раскраска ребер графа - это раскраска вершин его рёберного графа, а раскраска областей плоского графа – это раскраска вершин дуального графа. Тем не менее, другие проблемы раскраски графов часто ставятся и решаются в изначальной постановке. Причина этого частично заключается в том, что это даёт лучшее представление о происходящем и более показательно, а частично из-за того, что некоторые задачи таким образом решать удобнее (например, раскраска рёбер). Договоренность об использовании цветов происходит из традиции выделения цветом стран на политической карте. Она была обобщена на окраску областей плоского графа. Через дуальные графы эта модель распространилась и на раскраску вершин, а затем и на другие виды графов. В математическом и компьютерном представлении обычно в качестве цветов используются целые неотрицательные числа. Таким образом, мы можем использовать любой конечный набор в качестве “цветового набора”, и проблема раскраски графов зависит от количества цветов, а не от того, чем они являются.Слайд 39 Спиричева Н.Р.
Каждый многоугольный граф можно представить
себе как некоторую географическую карту, где грани- это страны, а
бесконечная грань- окружающий их океан. На такой карте все страны и океан раскрашиваются так, чтобы их можно было отличить друг от друга. Для этого страны с общей границей должны быть раскрашены в разные цвета. Если в нашем расnоряжении имеется достаточное колличество красок, это не составит никакого труда. Намного сложнее решить вопрос о наименьшем колличестве красок, достаточного дпя такого раскрашивания стран данной карты. Широко известное предположение состоит в том, что каждая карта может быть раскрашена с соблюдением требуемых условий при помощи четырех красок. Британский математик А. Кэпи, один из первых исспедователей теории графов, в 1879 г. опубликовал статью о проблеме четырех красок, оказавшуюся вполне уместной в nервом томе трудов Коропевского географического общества. Эту статью часто считают «свидетельством о рождении» проблемы четырех красок. Однако это не совсем правильно. Шотландскпй физик Фредерик Гутри рассказывал, что около 1850 г. эта проблема была достаточно популярна среди студентов-математиков в Лондоне и что его брат Фрэнсис Гутри обратил на нее внимание своего nреподавателя математика А. Де Моргана. Поначалу проблема не казалась слишком серьезной. Математики, по-видимому, рассматривали ее как почти очевидный факт. В дальнейшем появилось несколько неверных доказательств: проблема четырех красок, сбивающая с толку простотой своей формулировки, сопротивлялась всем усилиям самых выдающихся математиков. Большой интерес к теории гpaфов, возникший в связи с этой проблемой, способствовал' открытию многих важных результатов этой теории, поскольку они казались полезными для решения проблемы четырех красок.Слайд 40 Спиричева Н.Р.
Когда говорят о раскраске графов,
почти всегда подразумевают под этим раскраску их вершин, то есть
присвоение цветовых меток вершинам графа так, чтобы любые две вершины, имеющие общую грань, имели разные цвета. Так как графы, в которых есть петли, не могут быть раскрашены таким образом, они не являются предметом обсуждения. Терминология, в которой метки называются цветами, происходит от раскраски политических карт. Такие метки как красный или синий используются только когда число цветов мало, обычно же подразумевается, что метки являются целыми числами {1,2,3,...}. Раскраска с использованием k цветов называется k-раскраской. Наименьшее число цветов, необходимое для раскраски графа G называется его хроматическим числом и часто записывается как X(G). Иногда используется Y(G), с тех пор как X(G) обозначает Эйлерову характеристику. Подмножество вершин, выделенных одним цветом, называется цветовым классом, каждый такой класс формирует независимый набор. Таким образом, k-раскраска - это то же самое, что и разделение вершин на k независимых наборов.Слайд 41 Спиричева Н.Р.
В теории графов рёберной раскраской
графа называется назначение «цветов» рёбрам графа таким образом, что никакие
два сопряжённых ребра не имеют один и тот же цвет. Например, рисунок справа показывает рёберную раскраску графа в красный, синий и зелёный цвета. Рёберная раскраска — это один из видов различных типов раскраски графов. Задача рёберной раскраски задаётся вопросом, можно ли раскрасить рёбра заданного графа максимум в k различных цветов для заданного значения k или для минимального возможного числа цветов. Минимальное требуемое число цветов для раскраски рёбер заданного графа называется хроматическим индексом графа. Например, рёбра графа на иллюстрации можно раскрасить в три цвета, но нельзя раскрасить в два, так что граф имеет хроматический индекс три.Слайд 42 Спиричева Н.Р.
Граф-цикл может быть раскрашен в
два цвета если длина цикла чётна — просто используем поочерёдно
два цвета последовательно проходя рёбра цикла. Однако в случае нечётной длины потребуется три цвета. Рёбра полного графа Kn с n вершинами могут быть раскрашены n - 1 цветами, если n чётно. Это специальный случай теоремы Бараньяи. Сойфер даёт следующее геометрическое построение раскраски в этом случае: разместим n точек в углах и в центре правильного (n - 1)-угольника. Для каждого класса цвета выберем одно ребро, соединяющее центр и одну из вершин многоугольника, и все перпендикулярные ему рёбра, соединяющие пары вершин многоугольника. Однако, если n нечётно, требуется n цветов — каждый цвет можно использовать только для раскраски (n - 1)/2 рёбер, 1/n-ю часть всех рёбер. Некоторые авторы изучали рёберную раскраску нечётных графов, n-регулярных графов, в которых вершины представляют команды из (n - 1) игроков из общего числа 2n-1 игроков, и в которых рёбра представляют возможные пары этих команд (с одним игроком «вне игры» для судейства). В случае, когда n = 3 получаем хорошо известный граф Петерсена. Как объясняет Бигс, задача (для n = 6) состоит в том, что игроки хотят найти такое расписание, что команды играют каждую из шести игр в разные дни недели, исключая воскресенье для всех игроков. В математической формулировке, они хотят найти 6-цветную рёберную раскраску 6-регулярных графов O6. Когда n равно 3, 4 или 8, рёберная раскраска графа On требует n + 1 цветов, но для 5, 6 и 7 нужно только n цветов.Слайд 43 Спиричева Н.Р.
В теории графов тотальной раскраской
называется вид раскраски вершин и рёбер графа. Если не указано
явно другое, тотальная раскраска предполагается правильной в том смысле, что никакие смежные вершины и никакие смежные рёбра и вершины, лежщие на концах рёбер, не раскрашиваются в один и тот же цвет. Тотальное хроматическое число X(G) графа G — это наименьшее число цветов, необходимых для тотальной раскраски G. Тотальным графом T = T(G) графа G называется граф, в котором множество вершин графа T соответствуют вершинам и рёбрам графа G две вершины в T смежны тогда и только тогда, когда соответствующие элементы либо смежны в G, либо инцидентны. При таком определении тотальная раскраска становится (правильной) вершинной раскраской тотального графа.Слайд 44Структуры данных
Алгоритмы поиска путей в графе
Путь с минимальным количеством
промежуточных вершин
Алгоритм просматривает вершины графа в таком порядке:
соединённые
с исходной вершинойсоединённые с уже просмотренными, но ещё не просмотренные.
Слайд 45Структуры данных
Волновой алгоритм
Каждой вершине i приписывается два целых числа Times[i]
- временная метка и Previous [i] - метка предыдущей вершины
пути (начальное значение Times[i]=0, Previous [i]=0 для всех i).Заводятся два списка "фронта волны" NewFront и OldFront, а также переменная Time (текущее время).
OldFront:={ver1}; NewFront:={}; Time:=1.
Для каждой из вершин i, входящих в OldFront, просматриваются соседние вершины j, и если Times [j] = 0, то Times [j]=Time, NewFront := NewFront + {j}; в переменную Previous [j] заносится номер i.
Если NewFront = {}, то путь не существует, переход к шагу 8.
Если одна из веpшин совпадает с ver2, то найден кратчайший путь длины Time, переход к шагу 8.
OldFront:= NewFront; NewFront:={}; Time:=Time+1; возврат к шагу 4.
Восстанавливаем путь, проходя массив P.
Слайд 46Структуры данных
Под корректностью алгоритма здесь понимается, что:
алгоритм завершает работу
за конечное время;
если решение существует, то алгоритм находит правильное решение.
Слайд 47Структуры данных
Алгоритмы поиска путей в графе
Путь минимальной суммарной длины
во взвешенном графе с неотрицательными весами (алгоритм Дейкстры)
Функция находит путь
минимального веса в графе G=(V,E), заданном весовой матрицей w, у которой элемент wi j равен весу ребра, соединяющего i-ю и j-ю вершины. При этом предполагается, что все элементы wi j неотрицательны. Путь ищется из вершины номер u1 к вершине номер u2. Функция использует алгоритм Дейкстры. Для бесконечности используется число GM, его можно задавать в зависимости от конкретной задачи.Слайд 48Структуры данных
Алгоритмы поиска путей в графе
Алгоритм, по которому происходит
поиск, заключается в следующем:
всем веpшинам пpиписывается вес - вещественное число,
d(i)=GM для всех вершин кроме вершины с номером u1, а d(u1)=0; всем веpшинам пpиписывается метка m(i)=0;
вершина u1 объявляется текущей - t=u1;
для всех вершин у которых m(i)=0, пересчитываем вес по формуле: d(i):=min{d(i), d(t)+W[t,i]};
среди вершин для которых выполнено m(i)=0, ищем ту, для которой d(i) минимальна, если минимум не найден, т.е. вес всех “непомеченных” вершин равен бесконечности (GM), то путь не существует; ВЫХОД;
иначе найденную вершину c минимальным весом полагаем текущей и помечаем (m(t)=1);
если t = u2, то найден путь веса d(t),ВЫХОД;
переходим на шаг 4.
Слайд 49Структуры данных
Алгоритмы поиска путей в графе
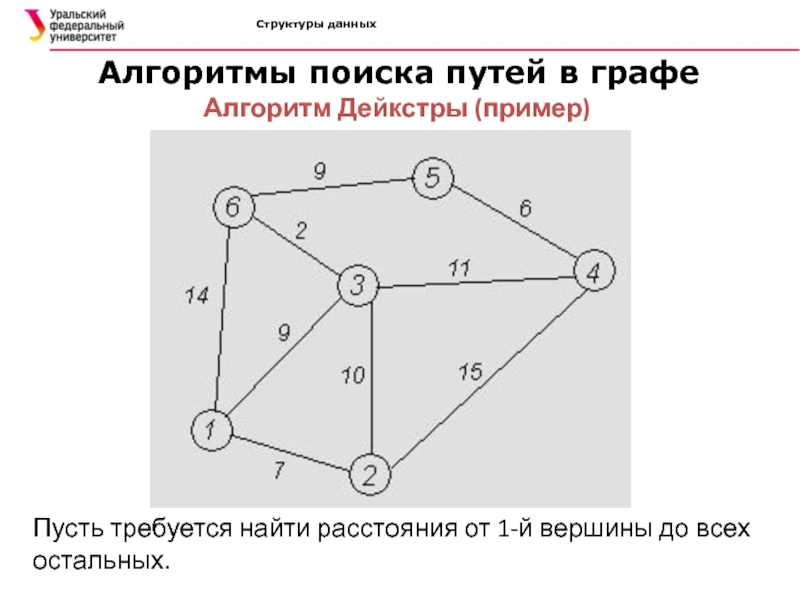
Алгоритм Дейкстры (пример)
Пусть требуется
найти расстояния от 1-й вершины до всех остальных.
Слайд 50Структуры данных
Алгоритмы поиска путей в графе
Алгоритм Дейкстры (пример)
Кружками обозначены
вершины, линиями — пути между ними (ребра графа). В кружках
обозначены номера вершин, над ребрами обозначена их «цена» — длина пути. Рядом с каждой вершиной красным обозначена метка — длина кратчайшего пути в эту вершину из вершины 1.Слайд 51Структуры данных
Алгоритмы поиска путей в графе
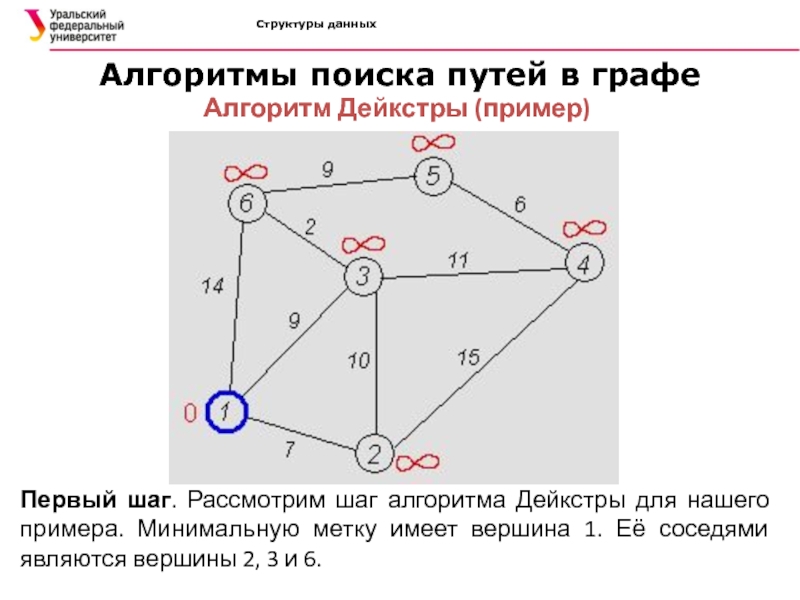
Алгоритм Дейкстры (пример)
Первый шаг.
Рассмотрим шаг алгоритма Дейкстры для нашего примера. Минимальную метку имеет
вершина 1. Её соседями являются вершины 2, 3 и 6.Слайд 52Структуры данных
Алгоритмы поиска путей в графе
Алгоритм Дейкстры (пример)
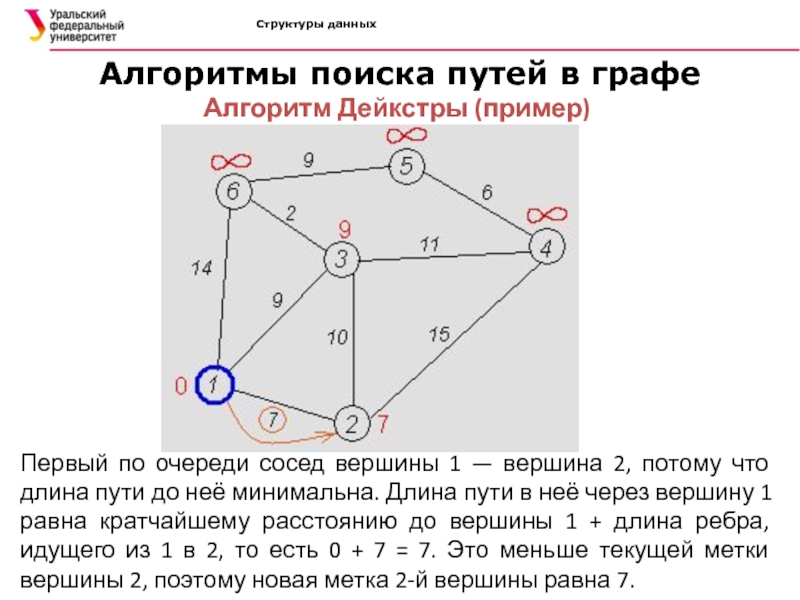
Первый по
очереди сосед вершины 1 — вершина 2, потому что длина
пути до неё минимальна. Длина пути в неё через вершину 1 равна кратчайшему расстоянию до вершины 1 + длина ребра, идущего из 1 в 2, то есть 0 + 7 = 7. Это меньше текущей метки вершины 2, поэтому новая метка 2-й вершины равна 7.Слайд 53Структуры данных
Алгоритмы поиска путей в графе
Алгоритм Дейкстры (пример)
Аналогичную операцию
проделываем с двумя другими соседями 1-й вершины — 3-й и
6-й.Слайд 54Структуры данных
Алгоритмы поиска путей в графе
Алгоритм Дейкстры (пример)
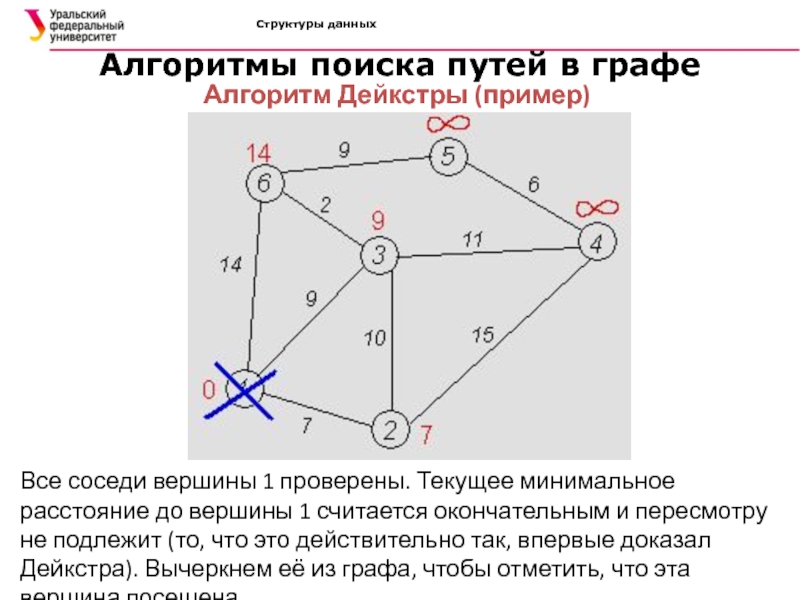
Все соседи
вершины 1 проверены. Текущее минимальное расстояние до вершины 1 считается
окончательным и пересмотру не подлежит (то, что это действительно так, впервые доказал Дейкстра). Вычеркнем её из графа, чтобы отметить, что эта вершина посещена.Слайд 55Структуры данных
Алгоритмы поиска путей в графе
Алгоритм Дейкстры (пример)
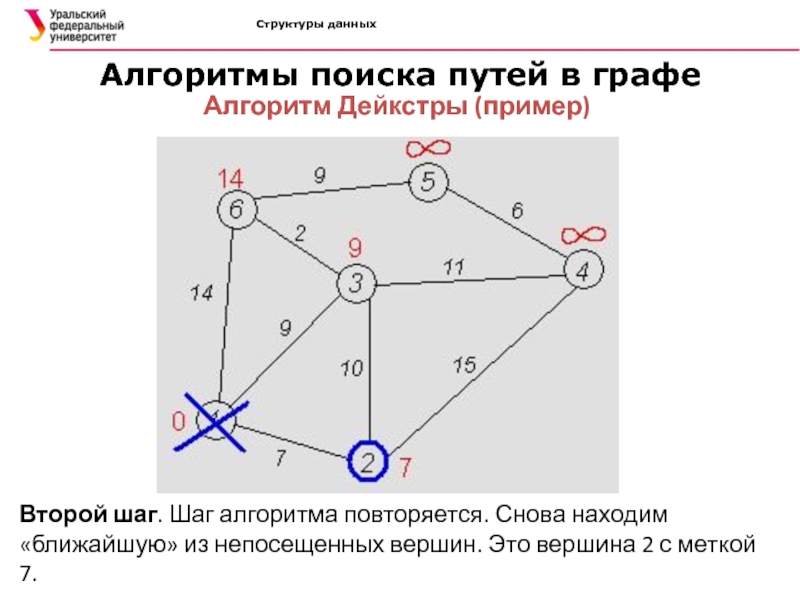
Второй шаг.
Шаг алгоритма повторяется. Снова находим «ближайшую» из непосещенных вершин. Это
вершина 2 с меткой 7.Слайд 56Структуры данных
Алгоритмы поиска путей в графе
Алгоритм Дейкстры (пример)
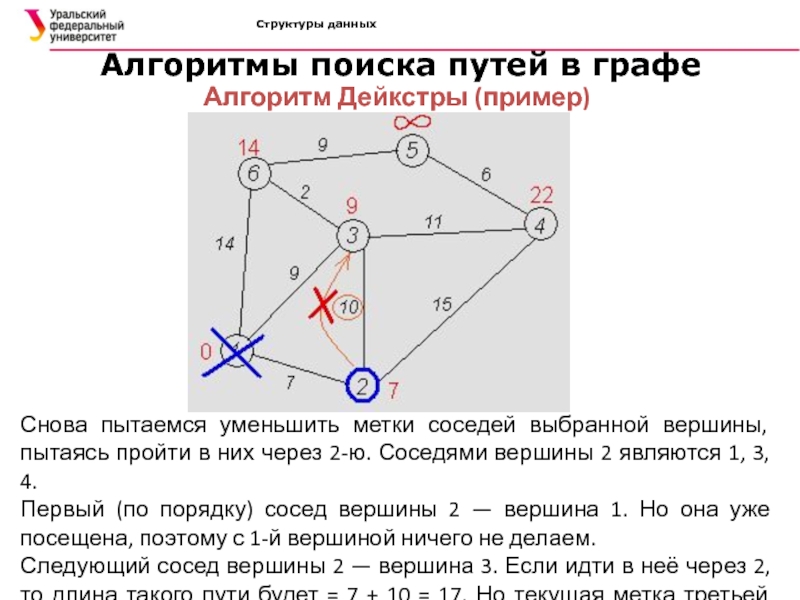
Снова пытаемся
уменьшить метки соседей выбранной вершины, пытаясь пройти в них через
2-ю. Соседями вершины 2 являются 1, 3, 4.Первый (по порядку) сосед вершины 2 — вершина 1. Но она уже посещена, поэтому с 1-й вершиной ничего не делаем.
Следующий сосед вершины 2 — вершина 3. Если идти в неё через 2, то длина такого пути будет = 7 + 10 = 17. Но текущая метка третьей вершины равна 9<17, поэтому метка не меняется.
Слайд 57Структуры данных
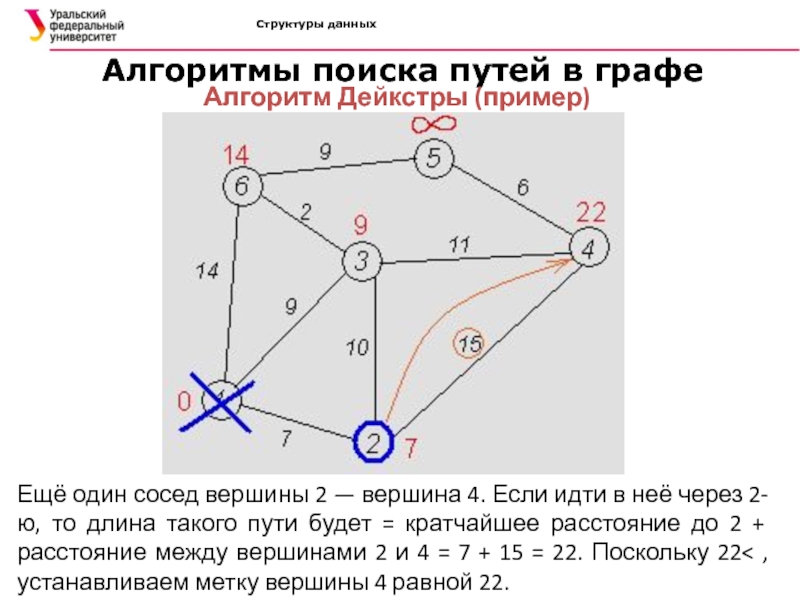
Алгоритмы поиска путей в графе
Алгоритм Дейкстры (пример)
Ещё один
сосед вершины 2 — вершина 4. Если идти в неё
через 2-ю, то длина такого пути будет = кратчайшее расстояние до 2 + расстояние между вершинами 2 и 4 = 7 + 15 = 22. Поскольку 22< , устанавливаем метку вершины 4 равной 22.Слайд 58Структуры данных
Алгоритмы поиска путей в графе
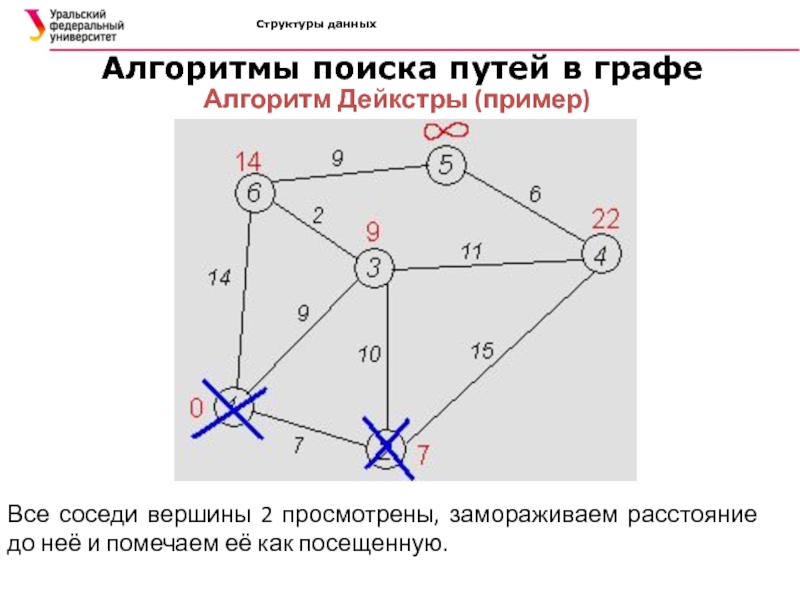
Алгоритм Дейкстры (пример)
Все соседи
вершины 2 просмотрены, замораживаем расстояние до неё и помечаем её
как посещенную.Слайд 59Структуры данных
Алгоритмы поиска путей в графе
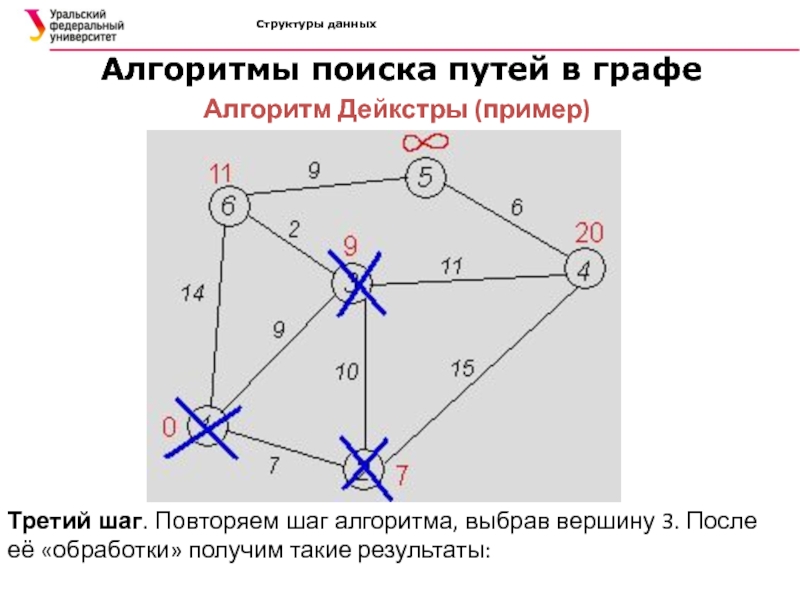
Алгоритм Дейкстры (пример)
Третий шаг.
Повторяем шаг алгоритма, выбрав вершину 3. После её «обработки» получим
такие результаты:Слайд 60Структуры данных
Алгоритмы поиска путей в графе
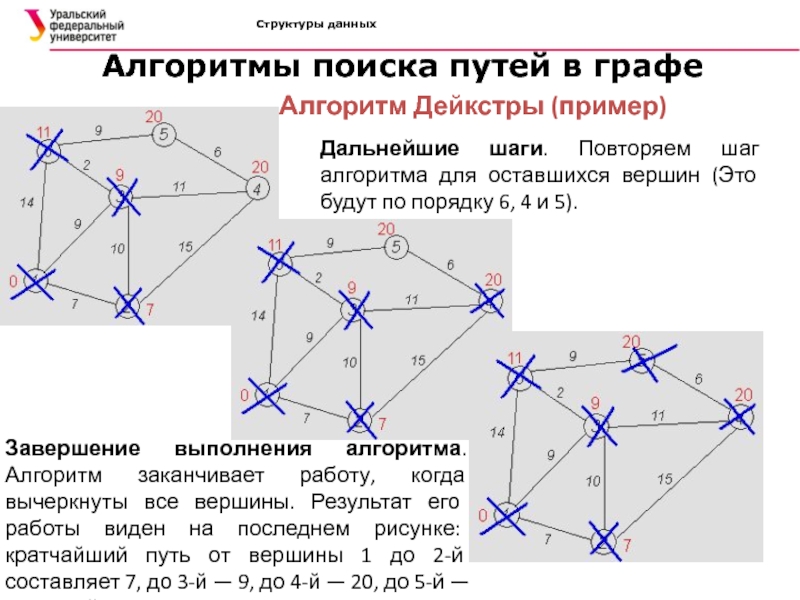
Алгоритм Дейкстры (пример)
Дальнейшие шаги.
Повторяем шаг алгоритма для оставшихся вершин (Это будут по порядку
6, 4 и 5).Завершение выполнения алгоритма. Алгоритм заканчивает работу, когда вычеркнуты все вершины. Результат его работы виден на последнем рисунке: кратчайший путь от вершины 1 до 2-й составляет 7, до 3-й — 9, до 4-й — 20, до 5-й — 20, до 6-й — 11.
Слайд 61Структуры данных
Алгоритмы поиска путей в графе
Путь минимальной суммарной длины
во взвешенном графе с произвольными весами для всех пар вершин
(алгоритм Флойда) Функция находит пути минимального веса в графе G=(V,E), заданном весовой матрицей w, у которой элемент wi j равен весу ребра, соединяющего i-ю и j-ю вершины. При этом полагаем, что W[i,i]=0 для всех i. Путь ищется для всех пар вершин графа. Для бесконечности используется число GM, его можно задавать в зависимости от конкретной задачи.Алгоритм Флойда предполагает последовательное преобразование матрицы весов W. В конечном итоге получаем матрицу, элементы d[i,j] которой представляют из себя вес минимального пути соединяющего i и j вершины.
Слайд 62Структуры данных
Алгоритмы поиска путей в графе
Нахождение K путей минимальной
суммарной длины во взвешенном графе с неотрицательными весами (алгоритм Йена)
Алгоритм предназначен для нахождения К путей минимальной длины во взвешенном графе между вершинами u1,u2. Ищутся пути, которые не содержат петель. Работа алгоритма начинается с нахождения кратчайшего пути, для этого будем использовать уже описанный алгоритм Дейкстры. Второй путь ищем, перебирая кратчайшие отклонения от первого, третий - кратчайшие отклонения от второго, и т.д.
Слайд 63Структуры данных
Алгоритмы поиска путей в графе
Алгоритм:
1. Найти минимальный путь
P1=(v11,...,v1L[1]). Положить k = 2. Включить P1 в результирующий список.
2.
Положить MinW равным бесконечности. Найти отклонение минимального веса от (k–1)-го кратчайшего пути Pk-1 для всех i=1,2,...,L[k-1], выполняя для каждого i шаги с 3-го по 6-й.3. Проверить, совпадает ли подпуть, образованный первыми i вершинами пути Pk-1, с подпутем, образованным первыми i вершинами любого из путей j=1,2,...,k–1). Если да, положить W[vk-1i,vji+1] равным бесконечности, в противном случае ничего не изменять (чтобы в дальнейшем исключить получение в результате одних и тех же путей).4. Используя алгоритм нахождения кратчайшего пути, найти пути от vk-1i к u2, исключая из рассмотрения корни (vk-11,...,vk-1i) (чтобы исключить петли), для этого достаточно положить равными бесконечности элементы столбцов и строк матрицы W, соответствующие вершинам, входящим в корень.
5. Построить путь, объединяя корень и найденное кратчайшее ответвление; если его вес меньше MinW, то запомнить его.
6. Восстановить исходную матрицу весов W и возвратиться к шагу 3.
7. Поместить путь минимального веса (MinW), найденный в результате выполнения шагов с 3 по 6, в результирующий список. Если k = K, то алгоритм заканчивает работу, иначе увеличить k на единицу и вернуться к шагу 2.
Слайд 64Структуры данных
1.Какими структурами данных можно представить в памяти древовидные структуры?
2.
Перечислите основные алгоритмы поиска путей в графах?
3. Какие основные классами
матриц предствляются графы в памяти компьютера?Контрольные вопросы























![СТРУКТУРЫ ДАННЫХ
Лектор
Спиричева Наталия Рахматулловна
Ст. преподаватель каф Структуры данных Графы Класс матриц смежности. Матрица смежности S=[sij]nxm невзвешенного графа определяется следующим Структуры данных Графы Класс матриц смежности. Матрица смежности S=[sij]nxm невзвешенного графа определяется следующим образом: Во взвешенном графе каждая единица заменяется](/img/tmb/3/246729/342785fa463a1b0de1a1c9f2f2d5699b-800x.jpg)







![СТРУКТУРЫ ДАННЫХ
Лектор
Спиричева Наталия Рахматулловна
Ст. преподаватель каф Структуры данных Волновой алгоритмКаждой вершине i приписывается два целых числа Times[i] - Структуры данных Волновой алгоритмКаждой вершине i приписывается два целых числа Times[i] - временная метка и Previous [i] -](/img/thumbs/f9443b0fb251b34e3ab4c715edf2d59b-800x.jpg)







![СТРУКТУРЫ ДАННЫХ
Лектор
Спиричева Наталия Рахматулловна
Ст. преподаватель каф Структуры данных Алгоритмы поиска путей в графе Алгоритм:1. Найти минимальный путь P1=(v11,...,v1L[1]). Структуры данных Алгоритмы поиска путей в графе Алгоритм:1. Найти минимальный путь P1=(v11,...,v1L[1]). Положить k = 2. Включить P1](/img/tmb/3/246729/1a9f88ec9165fda783af71cb4800973f-800x.jpg)