Слайд 2Делитель натуральных чисел
Делителем натурального числа а называют натуральное число на
которое а делится без остатка.
18 делится на 1, 2, 3,
6, 9, 18 без остатка поэтому 1, 2, 3, 6, 9, 18 – делители числа 18.
15 делится на 1, 3, 5, 15 без остатка поэтому 1, 3, 5, 15 делители числа 15.
7 делится на 1, 7 без остатка поэтому 1 и 7 – делители числа 7.
Число 1 является делителем любого натурального числа.
Наибольший делитель данного натурального числа равен самому числу.
Слайд 3 Кратное натуральных чисел
Кратным натурального числа b называют натуральное число,
которое делится на b без остатка.
5, 10, 15, 20, 25…
- кратные числу 5, т.к. они делятся на 5 без остатка.
13, 26, 39, 52… - кратные числу 13, т.к. они делятся на 13 без остатка.
Любое натуральное число имеет бесконечно много кратных.
Чтобы получить кратное данному числу надо это число умножить на какое-нибудь натуральное число.
Наименьшее кратное данного натурального числа равно самому числу.
Слайд 4Делимость суммы на натуральное число
Если каждое из слагаемых делится на
натуральное число, то и сумма делится на натуральное число.
(
а + b) : с = а : с + b : с
Например:
(12 + 60) : 12 = 12 : 12 + 60 : 12 = 1 + 5 = 6
(49а + 35с + 77) : 7 = 49а : 7 + 35с : 7 + 77 : 7 = 7а + 5с + 11
Можно не писать
(48 + 32) : 8 = 48 : 8 + 32 : 8 = 6 + 4 = 10
(52 + 26 + 39):13 = 52 : 13 + 26 : 13 + 39 : 13 = 4+2+3=9
Слайд 5Выполнить деление суммы на натуральное число
( а + b) :
с = а : с + b : с
(21 +
56) : 7 =
(81 + 36) : 9 =
(66 + 176) : 11 =
(33 + 209) : 11 =
(24х + 6х) : 3 =
(34х + 17х + 68) : 17 =
(104х + 26х + 39х) : 13 =
(100+50):25=
Слайд 6Домашняя работа
Вычислить, используя формулу
( а + b) : с =
а : с + b : с
(342 * 132) :
171 =
(721 + 567) : 7 =
(12 * 84) : 21 =
(217 + 56) : 7 =
(651 * 11) : 21 =
(126 + 63) : 7 =
Слайд 7Делимость произведения на натуральное число
Если один из множителей делится на
натуральное число, то и произведение делится на натуральное число.
( а
* b) : с = ( а : с) * b = а * ( b : с)
Например:
(65 * 52) : 13 = 65 : 13 * 52 = 5 * 52 = 260
(65а * 130) : 13 = 65а : 13 * 130 = 5а *130 =650а
Слайд 8Разделить произведение на натуральное число
( а * b) : с
= ( а : с) * b = а *
( b : с)
(42 * 132) : 21 =
(63 * 92) : 46 =
(86 * 132) : 66 =
(412 * 84) : 21 =
(30 * 143 ) : 11 =
(420 * 332) : 210 =
(174 * 52) : 26 =
Слайд 9Проверь себя.
Вычислить, используя удобный способ.
(342 * 132) :
171 = 342 : 171 * 132 = 264
(721+567)
:7 = 721 : 7 + 567 : 7 =103 +81 =184
(12 * 84) : 21 = 84 : 21 * 12 = 48
(217 + 56) : 7 = 217 : 7 + 56 : 7 = 31+ 8 = 49
(651 * 11) : 21 = 651 : 21 * 11 = 31 * 11 = 341
(126 + 63) : 7 = 126 : 7 + 63 : 7 =18 + 9 = 27
Слайд 10Вопросы урока
Какое число мы называем делителем?
Назовите самый большой и самый
маленький делитель данного числа
Какое число мы называем кратным?
Назовите самое большое
и самое маленькое кратное данного числа
Как разделить сумму на число?
Когда произведение делится на число?
Слайд 11Ответь на вопросы
Какое число называют делителем?
Какое число называют кратным?
Когда сумма
делится на число + формула?
Когда произведение делится на число +
формула?
Выпиши все делители числа 126
Вычисли:
(21 + 63) : 3 =
(72 + 18) : 9 =
(22 + 121) : 11 =
(34х + 17х + 68) : 17 =
Слайд 12Задание:
Запишите, какие из чисел
42, 66, 1020, 115,
1750, 232, 150, 515, 240, 909, 212, 101, 171, 306,
327
делятся без остатка:
а) на 2; б) на 5; в) на 10. г) на 4
д) на 25, е) на 6, ж) на 3, з) на 9
Придумай трехзначное число, которое:
а) делится на 3 и на 5,, но не делится на 10
б) делится на 9 и 10, но не делится на 25
в) делится на 2 и на 9, но не делится на 5
г) не делится ни на 2, ни на 3, ни на 5, ни на 9
Слайд 13Ответь на вопросы
Какое число называют делителем?
Делителем натурального числа а называют
натуральное число на которое а делится без остатка.
Какое число называют
кратным?
Кратным натурального числа b называют натуральное число, которое делится на b без остатка.
Когда сумма делится на число?
Если каждое из слагаемых делится на натуральное число, то и сумма делится на натуральное число.
Когда произведение делится на число?
Если один из множителей делится на натуральное число, то и произведение делится на натуральное число.
Слайд 14Признаки делимости на 2,5,10
Все натуральные числа запись которых оканчивается четной
цифрой делится на 2.
Все натуральные числа запись которых оканчивается цифрой
5 или цифрой 0 делится на 5.
Все натуральные числа запись которых оканчивается цифрой 0 делится на 10.
Слайд 15Признаки делимости на 3 и 9
Если сумма цифр делится на
3, то и само число делится на 3.
522 делится на
3 так как 5 + 2 + 2 = 9, а 9 : 3 = 3
8136 делится на 3 так как 8 + 1 + 3 + 6 = 18, а 18 делится на 3
Если сумма цифр делится на 9, то и само число делится на 9.
1728 делится на 9, т.к. 1 + 7 + 2 + 8 = 18, а 18 делится на 9
8748 делится на 9, т.к. 8 + 7 + 4 + 8 = 27, а 27 делится на 9
Слайд 16Ответь на вопросы
Когда число делится на 2?
Все натуральные числа запись
которых оканчивается четной цифрой делится на 2.
Когда число делится на
3?
Если сумма цифр делится на 3, то и само число делится на 3.
Когда число делится на 5?
Все натуральные числа запись которых оканчивается цифрой 5 или цифрой 0 делится на 5.
Когда число делится на 9?
Если сумма цифр делится на 9, то и само число делится на 9.
Когда число делится на 10?
Все натуральные числа запись которых оканчивается цифрой 0 делится на 10.
Слайд 17Простые и составные числа
4 делится на – 1, 2, 4.
6
делится на – 1, 2, 3, 6.
8 делится на –
1, 2, 4, 8.
9 делится на – 1, 3, 9.
10 делится на – 1, 2, 5, 10.
12 делится на – 1, 2, 3, 4, 6, 12.
14 делится на – 1, 2, 7, 14.
15 делится на – 1, 3, 5, 15.
16 делится на – 1, 2, 4, 8, 16.
18 делится на – 1, 2, 3, 6, 9, 18.
20 делится на – 1, 2, 4, 5, 10, 20.
2 делится на – 1, 2.
3 делится на – 1, 3.
5 делится на – 1, 5.
7 делится на – 1, 7.
11 делится на – 1, 11.
13 делится на – 1, 13.
17 делится на – 1, 17.
19 делится на – 1, 19.
23 делится на – 1, 23.
29 делится на – 1, 29.
31 делится на – 1, 31.
Слайд 18Простые и составные числа
Натуральные числа, которые имеют больше двух различных
делителей, называют составными.
Натуральные числа, которые делятся только на 1 и
на себя, то есть имеют только два делителя, называют простыми числами.
Число 1 не является простым числом, так как оно имеет только один делитель.
Слайд 19Вопросы урока
Какие числа называют простыми?
Натуральные числа, которые делятся только на
1 и на себя, то есть имеют только два делителя,
называют простыми числами.
Какие числа называют составными?
Натуральные числа, которые имеют больше двух различных делителей, называют составными.
Число 1 – это простое или составное число?
Число 1 не является ни простым ни составным числом
Слайд 20Разложение составных чисел на простые множители
2376 : 2
1188 : 2
594 : 2
297 : 3
99 : 3
33 : 3
11 : 11
1
2376=23*33*11
6885 : 3
2295 : 3
765 : 3
255 : 3
85 : 5
19 : 19
1
6885 = 34*5*19
Слайд 21Наибольший общий делитель.
Наибольшим общим делителем нескольких натуральных чисел
называется наибольшее натуральное число на которое данные числа делятся без
остатка.
Например:
57 делится на 1, 3, 19, 57
114 делится на 1, 2 ,3 ,6, 19, 57, 114
342 делится на 1, 2, 3, 6, 19, 57, 114, 342
НОД(57, 114, 342) = 57
Слайд 22Взаимно простые числа.
Числа называются взаимно простые, если их наибольший общий
делитель равен 1.
Например:
34 делится на 1, 2, 17, 34
46
делится на 1, 2, 23, 46
НОД(34, 46) = 1
Слайд 23Как найти НОД?
Чтобы найти НОД для данных чисел надо
Разложить числа
на простые множители
Выбрать множители которые есть в разложении каждого числа
Перемножить
выбранные множители. Произведение общих множителей и будет наибольшим общим делителем для данных чисел.
Слайд 24 Найти НОД(237, 688)
238 : 2
119 : 7
17 :
17
1
688 : 2
344 : 2
172 : 2
86
: 2
43 : 43
1
НОД(238, 688) = 2
Слайд 25 Найти НОД(186, 124)
186 : 2
93 : 3
31
: 31
1
124 : 2
62 : 2
31
: 31
1
НОД(186, 124) = 2 * 31 = 62
Слайд 26 Найти НОД(2376, 6885)
2376 : 2
1188 : 2
594 :
2
297 : 3
99 : 3
33
: 3
11 : 11
1
6885 : 3
2295 : 3
765 : 3
255 : 3
85 : 5
19 : 19
1
НОД(2376, 6885) = 3 * 3 * 3 = 27
Слайд 27Класная работа
НОД(78, 195) =
НОД(35, 18) =
НОД(36, 54, 72) =
НОД(231, 273)
=
НОД( 49, 48) =
НОД(50, 75, 60) =
НОД (520, 468) =
НОД (814, 4440) =
НОД (855, 11400) =
НОД (40, 100, 180) =
НОК (12,30)=
НОК (28, 35, 140)=
НОК (72, 90)=
НОК (25,100)=
НОК (18, 54)=
НОК (48, 126, 150)=
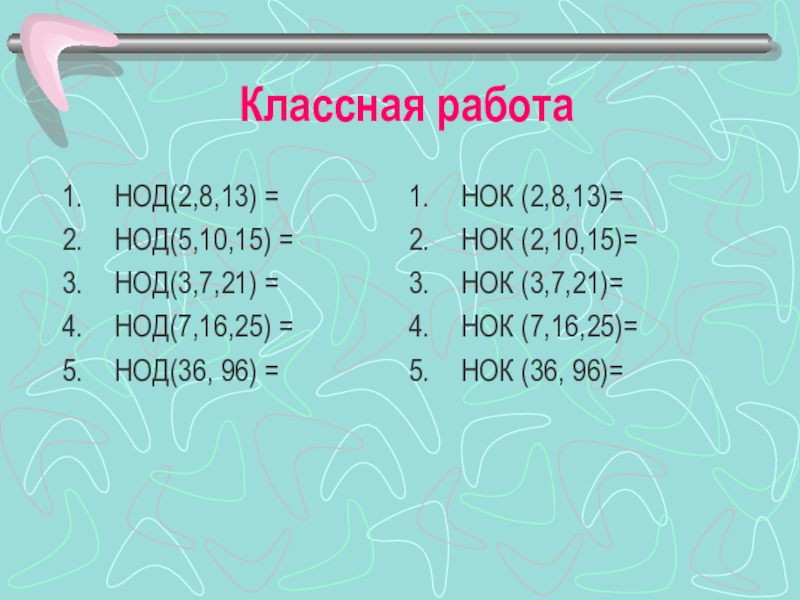
Слайд 28Классная работа
НОД(2,8,13) =
НОД(5,10,15) =
НОД(3,7,21) =
НОД(7,16,25) =
НОД(36, 96) =
НОК (2,8,13)=
НОК (2,10,15)=
НОК
(3,7,21)=
НОК (7,16,25)=
НОК (36, 96)=
Слайд 29Домашняя работа
НОД(2,4,5) =
НОД(2,6,12) =
НОД(3,7,14) =
НОД(180,396) =
НОД( 49, 21) =
НОК (2,4,5)=
НОК
(2,6,12)=
НОК (3,7,14)=
НОК (180,396)=
НОК (49, 21)=
Слайд 30Наименьшее общее кратное. (НОК)
Наименьшим общим кратным натуральных чисел называется
самое маленькое натуральное число которое делится на данные числа без
остатка.
Например:
24 – ему кратны 24, 48, 72, 96, 120, 144, 168, …
42 – ему кратны 42, 84, 126, 168,210,…
НОК(24, 42) = 168
Слайд 31Способы нахождения НОК.
Чтобы найти НОК для данных натуральных чисел, надо:
Разложить
на простые множители данные числа
Одно число взять все, а из
разложения второго числа только не достающие множители
Перемножить выбранные числа. Результат умножения и будет наименьшим общим кратным для данных чисел.
Слайд 32Контрольная работа
1. Напиши определения НОД и НОК
2. Какие числа называются
взаимно простыми?
3. Вычисли НОД и НОК для:
1, 2, 22
1, 7,
19
63, 126
11, 121
3, 7, 28
4. Приведите пример натурального двузначного четного числа, меньшего 50, которое делится на 7 и 21
5. Напишите наименьшее натуральное трехзначное число, кратное 15 и 9.