Свойство биссектрисы угла

Содержание

1. Свойство биссектрисы угла
2. Рассмотреть теорему о свойстве биссектрисы угла
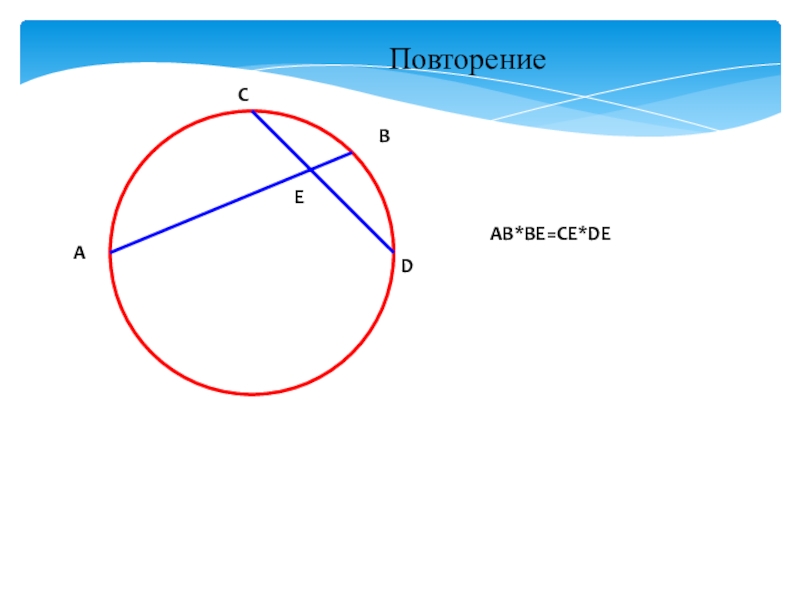
3. ABCDEAB*BE=CE*DEПовторение
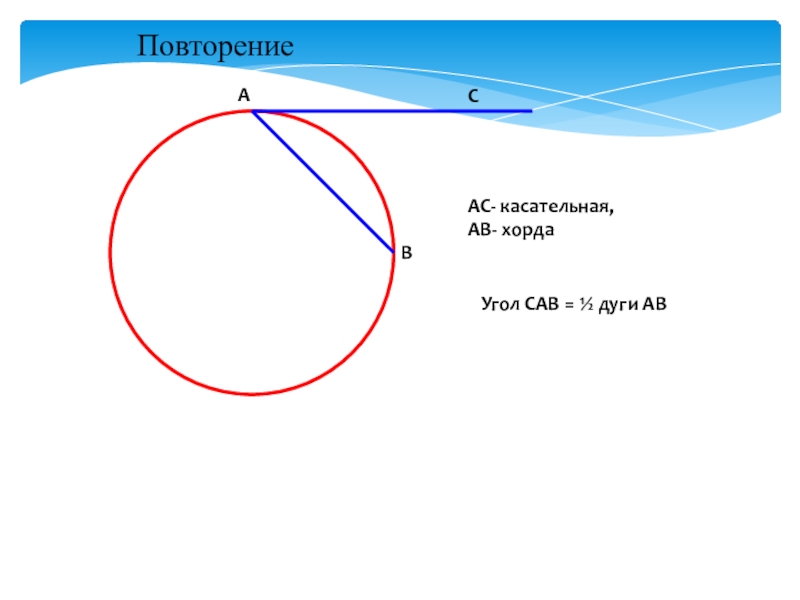
4. CBAAC- касательная, АВ- хордаУгол САВ = ½ дуги АВПовторение
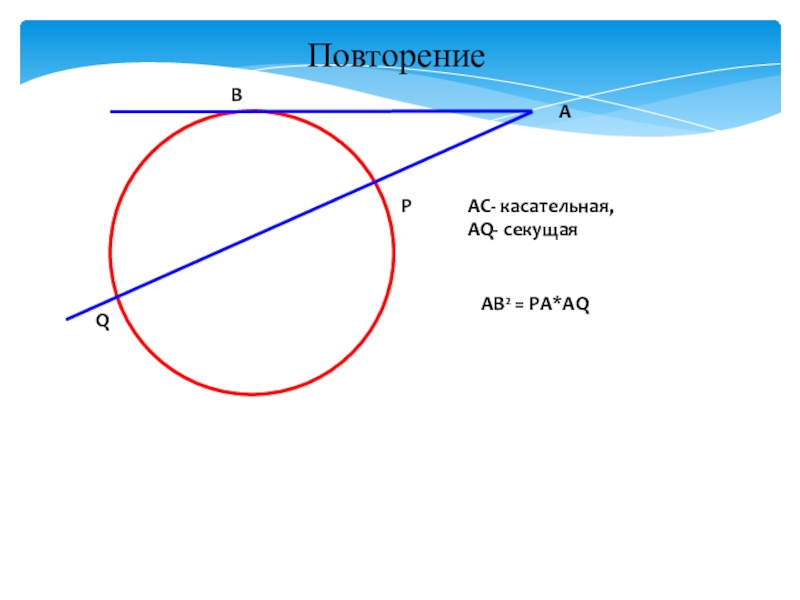
5. РBAAC- касательная, АQ- секущаяАВ² = РА*AQQПовторение
6. Вариант I1. Точки А, В, С лежат
7. C каждым треугольником связаны четыре точки: •
8. Свойство биссектрисыКаждая точка биссектрисы неразвёрнутого угла равноудалена
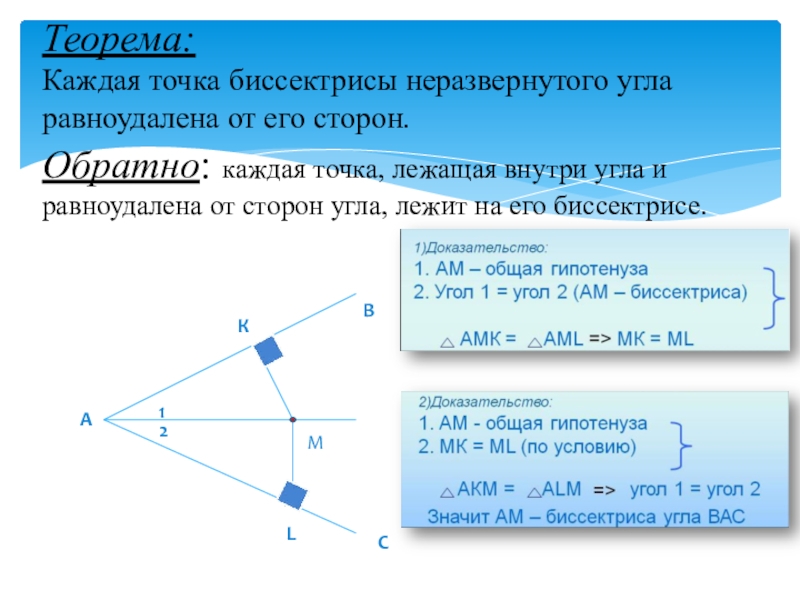
9. Теорема: Каждая точка биссектрисы неразвернутого угла равноудалена
10. Следствие: Биссектрисы треугольника пересекаются в одной
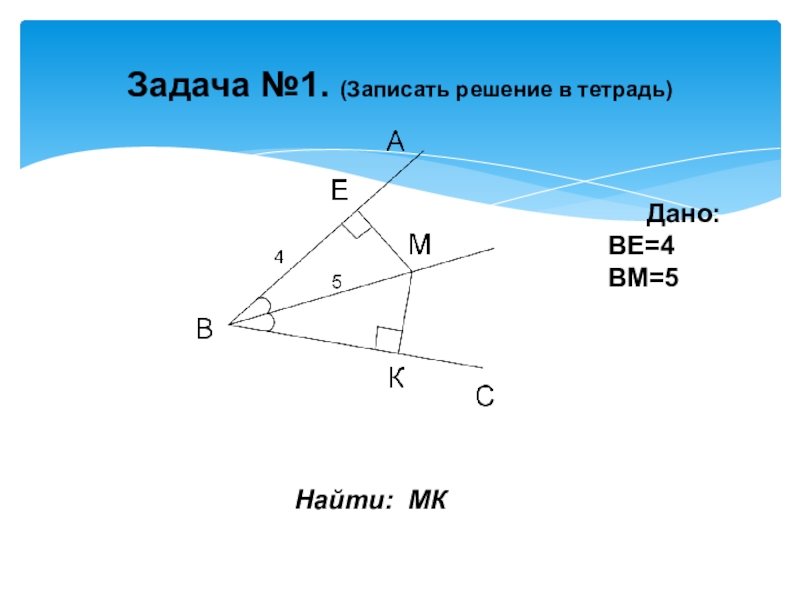
11. Задача №1. (Записать решение в тетрадь)Найти: МК Дано:ВЕ=4ВМ=5
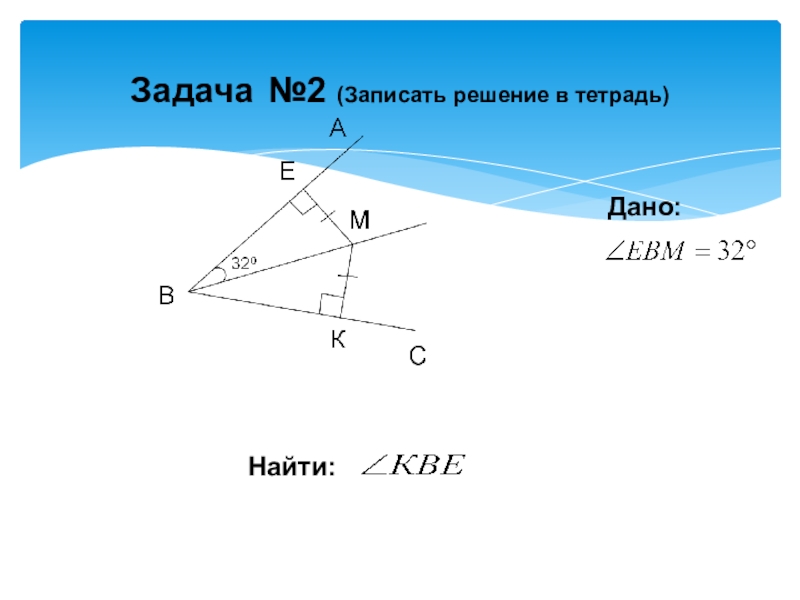
12. Задача №2 (Записать решение в тетрадь)Дано:Найти:
13. Задача № 676 (б)
14. Работа с учебникомПункт 74, Задачи № 678 (а) дополнительно.
15. Домашнее задание: п.74 читать, теоремы выучить.(((
16. Скачать презентанцию

Рассмотреть теорему о свойстве биссектрисы угла и её следствие. Научиться применять данные теоремы и следствие при решении задач.Цели урока:

Главная
Разное
Свойство биссектрисы угла

Слайды и текст этой презентации

Слайд 1 Свойство биссектрисы угла
Четырнадцатое апреля
Классная работа

Слайд 2 Рассмотреть теорему о свойстве биссектрисы угла и её следствие.

Научиться применять данные теоремы и следствие при решении задач.

Цели урока:

Рассмотреть теорему о свойстве биссектрисы угла и её следствие. Научиться применять данные теоремы и следствие при

Слайд 3A
B
C
D
E
ABBE=CEDE
Повторение

Слайд 4C
B
A
AC- касательная,
АВ- хорда
Угол САВ = ½ дуги АВ
Повторение

Слайд 5Р
B
A
AC- касательная,
АQ- секущая
АВ² = РА*AQ
Q
Повторение

Слайд 6Вариант I
1. Точки А, В, С лежат на окружности с

центром О,
угол АОВ = 80°, дуга АС : дуга

ВС = 2 : 3.
Найдите углы треугольника АВС.
2. Хорды АВ и СD пересекаются в точке K, причем хорда АВ делится точкой К на отрезки, равные 10 см и 6 см.
На какие отрезки точка K делит хорду СD, если СD > АВ на 3 см?

Самостоятельная работа

Вариант I1. Точки А, В, С лежат на окружности с центром О, угол АОВ = 80°, дуга

Слайд 7
C каждым треугольником связаны четыре точки:

• точка пересечения медиан;

• точка пересечения биссектрис;
• точка пересечения серединных перпендикуляров;
•

точка пересечения высот.

Эти четыре точки называют замечательными точками треугольника.
Почему они «Замечательные»?
Это нам и предстоит узнать.

C каждым треугольником связаны четыре точки: • точка пересечения медиан; • точка пересечения биссектрис; • точка пересечения

Слайд 8Свойство биссектрисы
Каждая точка биссектрисы неразвёрнутого угла равноудалена от его сторон.

Обратно:

Каждая

точка, лежащая внутри угла и равноудалённая от сторон угла, лежит

на его биссектрисе.

Свойство биссектрисыКаждая точка биссектрисы неразвёрнутого угла равноудалена от его сторон.Обратно:Каждая точка, лежащая внутри угла и равноудалённая от

Слайд 9Теорема: Каждая точка биссектрисы неразвернутого угла равноудалена от его сторон. Обратно:

каждая точка, лежащая внутри угла и равноудалена от сторон угла,

лежит на его биссектрисе.

Теорема: Каждая точка биссектрисы неразвернутого угла равноудалена от его сторон. Обратно: каждая точка, лежащая внутри угла

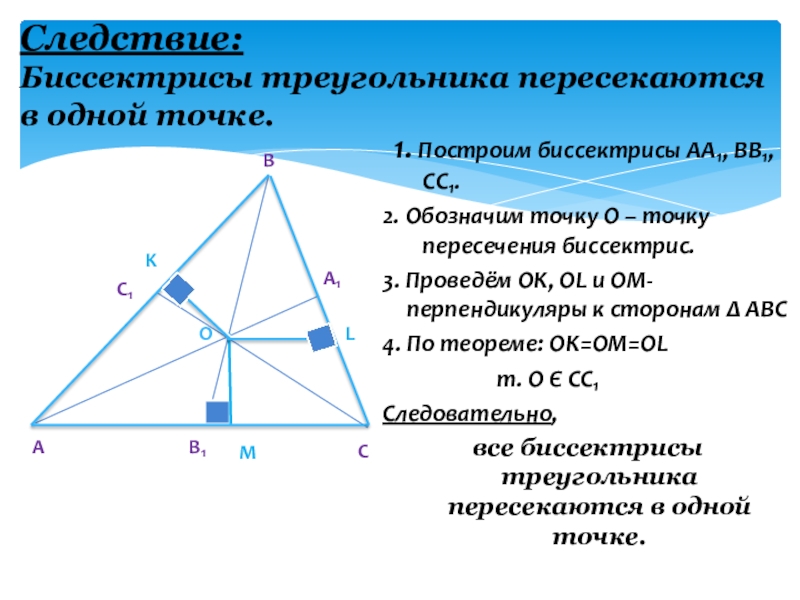
Слайд 10Следствие: Биссектрисы треугольника пересекаются в одной точке.
1. Построим биссектрисы

АА₁, BB₁, CC₁.
2. Обозначим точку O – точку пересечения

биссектрис.
3. Проведём OK, OL и OM-перпендикуляры к сторонам Δ ABC
4. По теореме: OK=OM=OL
т. О Є СС₁
Следовательно,
все биссектрисы треугольника пересекаются в одной точке.

Следствие: Биссектрисы треугольника пересекаются в одной точке. 1. Построим биссектрисы АА₁, BB₁, CC₁. 2. Обозначим точку

Слайд 11Задача №1. (Записать решение в тетрадь)
Найти: МК

Дано:
ВЕ=4
ВМ=5

Слайд 12Задача №2 (Записать решение в тетрадь)
Дано:

Найти:

Слайд 13 Задача № 676 (б) Cтороны угла А, равного 90°,

касаются окружности с центром О и радиусом r, ОА =

14 дм. Найдите: r.

Решение:
Проведём радиусы OP и OH из центра окружности в точки касания.
2. AO – биссектриса угла
Δ AOP – прямоугольный.
По теореме Пифагора:
AO²=OP²+AP²
AO²=r²+r²,
2r²=14², r=7√2.
Ответ: r=7√2дм.