Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Свойство касательной. Центральные углы и углы, вписанные в окружность
Содержание
- 1. Свойство касательной. Центральные углы и углы, вписанные в окружность
- 2. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМОЙ И ОКРУЖНОСТИ
- 3. Как вы думаете, сколько общих точек могут иметь прямая и окружность?О
- 4. ОСначала вспомним как задаётся окружностьОкружность (О, r)r – радиусrABАВ – хорда СDCD - диаметр
- 5. Исследуем взаимное расположение прямой и окружности в
- 6. Второй случай:ОНrодна общая точкаd = rd – расстояние от центра окружности до прямойdАВАВ – касательная
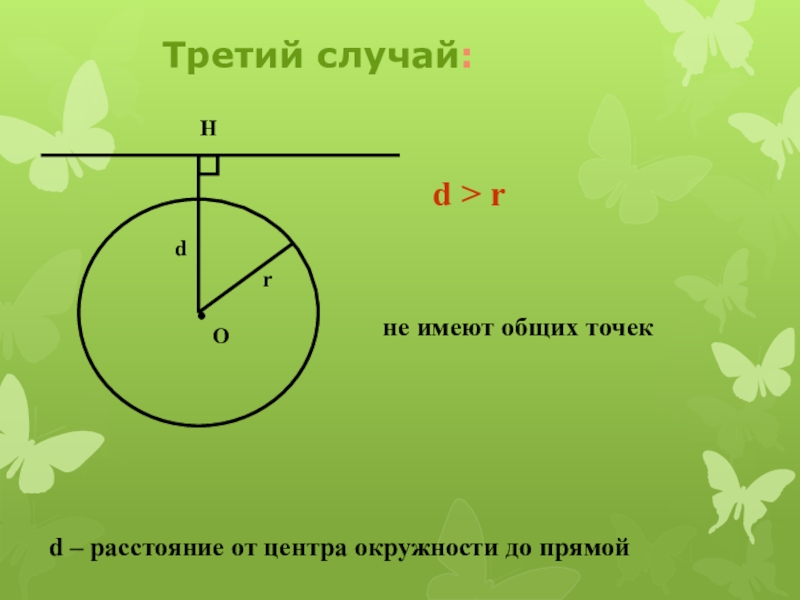
- 7. Третий случай:ОHdrd > rd – расстояние от центра окружности до прямойне имеют общих точек
- 8. Сколько общих точек могут иметь прямая и
- 9. Касательная к окружностиОпределение: Прямая, имеющая с окружностью
- 10. Слайд 10
- 11. Признак касательной: Если прямая проходит через
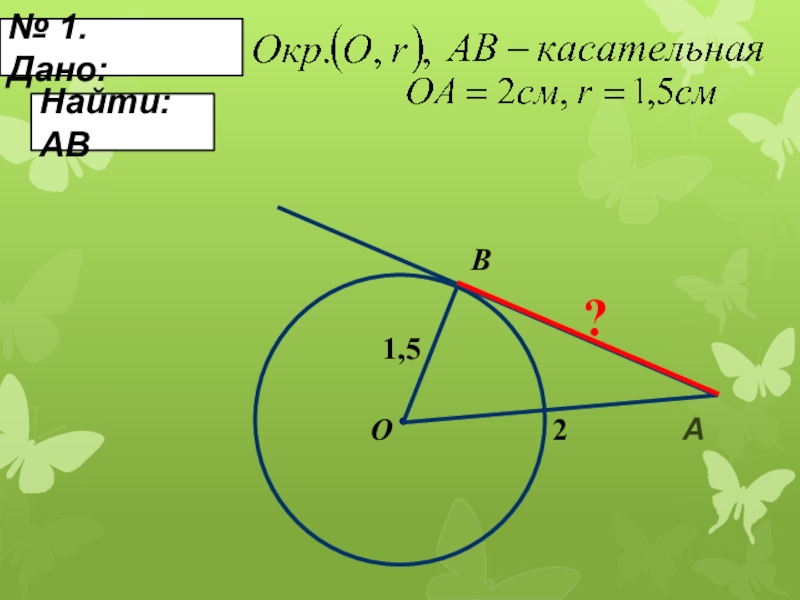
- 12. Найти: АВ№ 1. Дано:BОА21,5?
- 13. BОА21,5?1. Рассмотрим АОВ- прямоугольный(?)2.
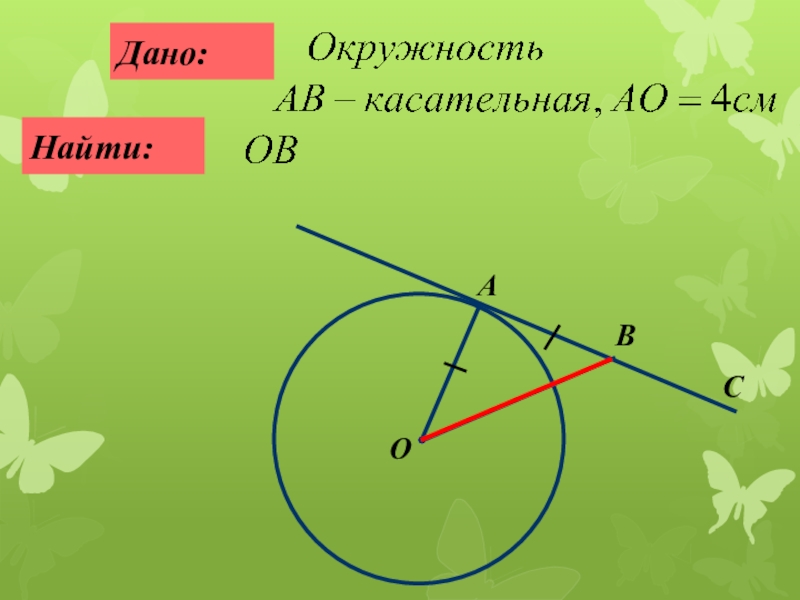
- 14. № 2. Дано:Найти:АОСBК4,5?АB, АС- касательные
- 15. АОСBК4,5?1. Рассмотрим -ки
- 16. Дано:Найти:СBОА
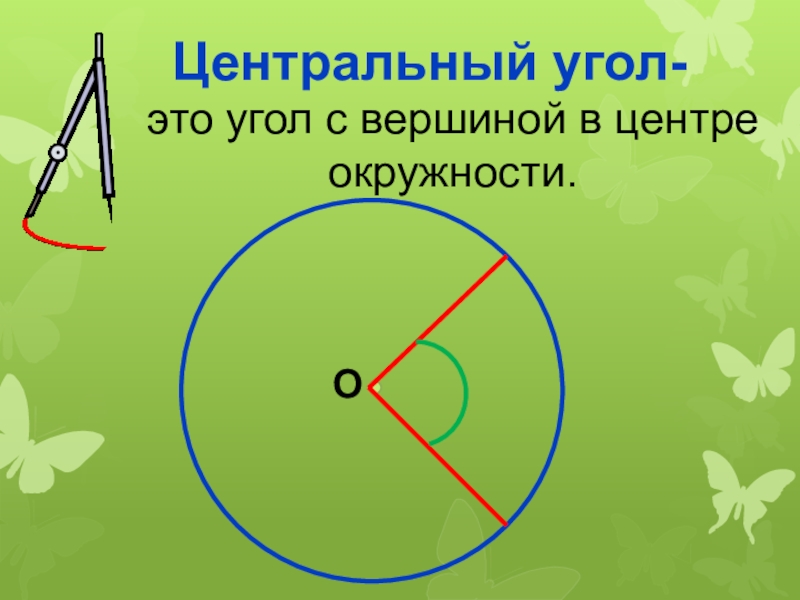
- 17. Центральный угол-это угол с вершиной в центре окружности.О
- 18. Дуга окружности, соответствующая центральному углуэто часть окружности,
- 19. Вписанный уголЭто угол, вершина которого лежит на окружности, а стороны пересекают окружность.САВ
- 20. Теорема о вписанном углеУгол, вписанный в окружность,
- 21. Решение упражненийУчтите, что вся окружность составляет дугу равную 360°
- 22. Найдите Х№175x285О
- 23. Найдите Хx145№2215О
- 24. Найдите Хx45№390О
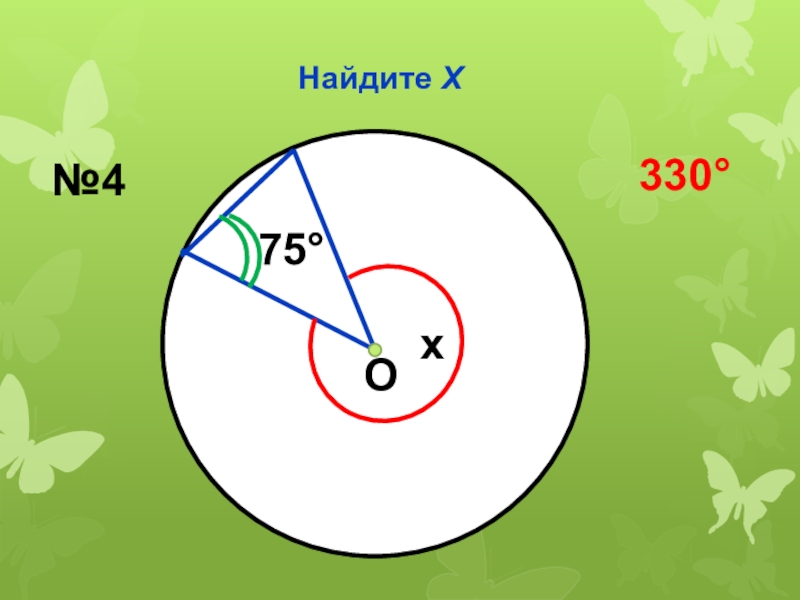
- 25. Найдите ХО75x№4330
- 26. Найдите ХО x40№5140
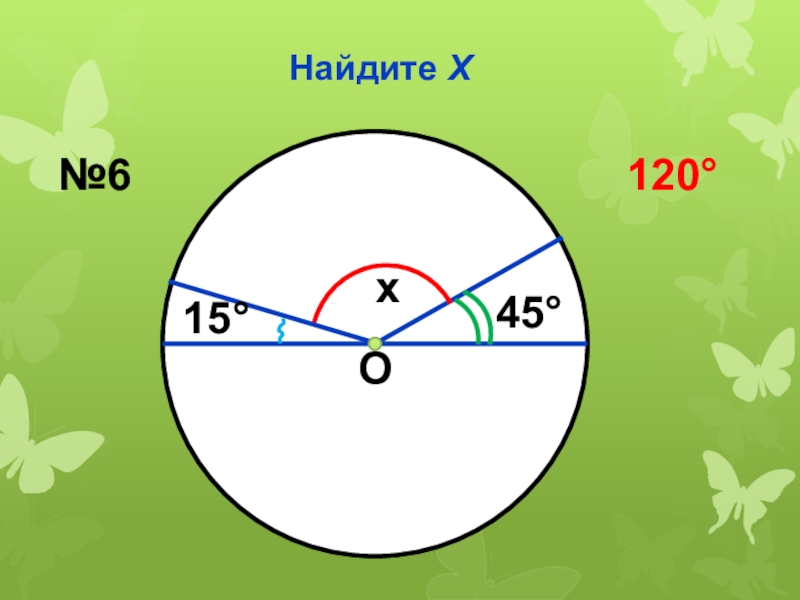
- 27. Найдите ХО x4515№6120
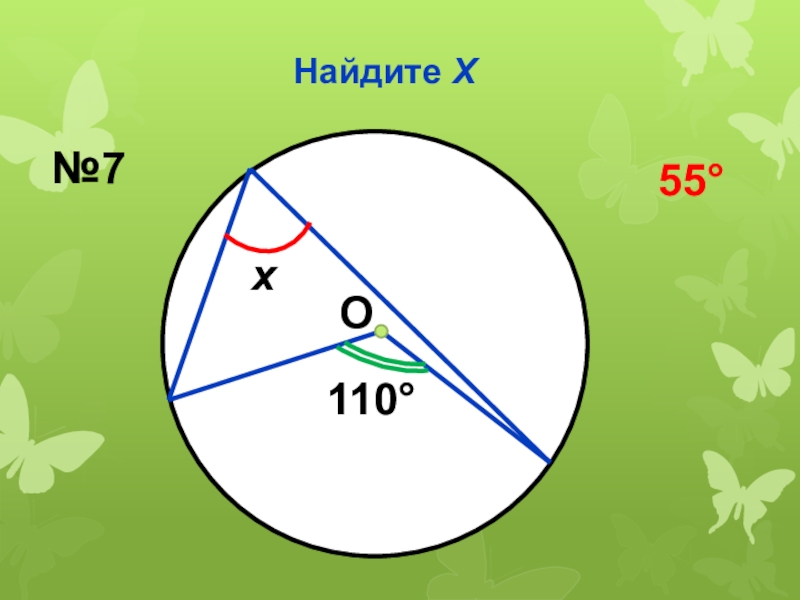
- 28. Найдите ХО110х№755
- 29. Найдите ХХ75№8150О
- 30. Найдите ХО120Х№9240
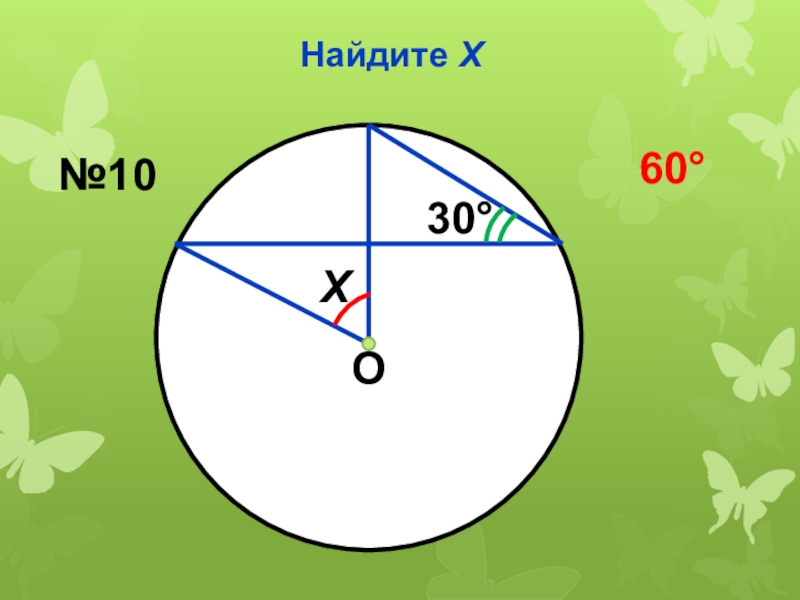
- 31. Найдите ХОХ30№1060
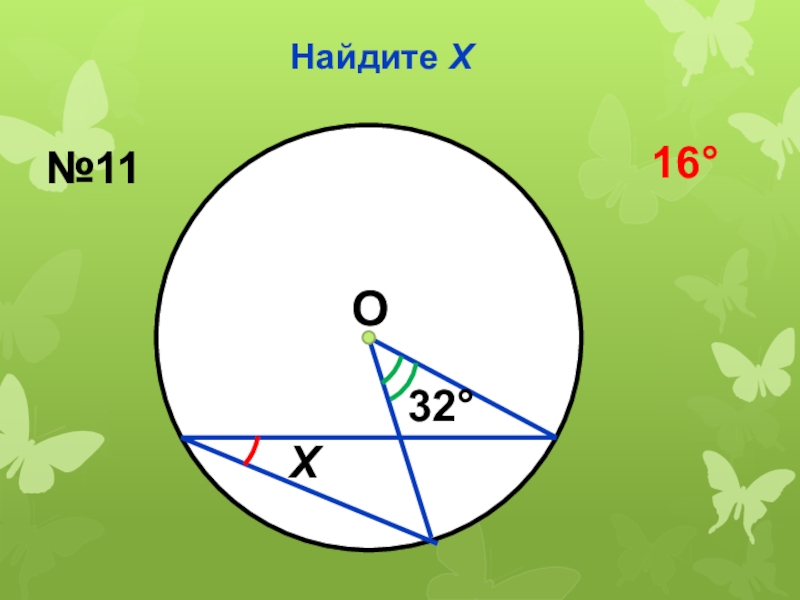
- 32. Найдите ХО32Х№1116
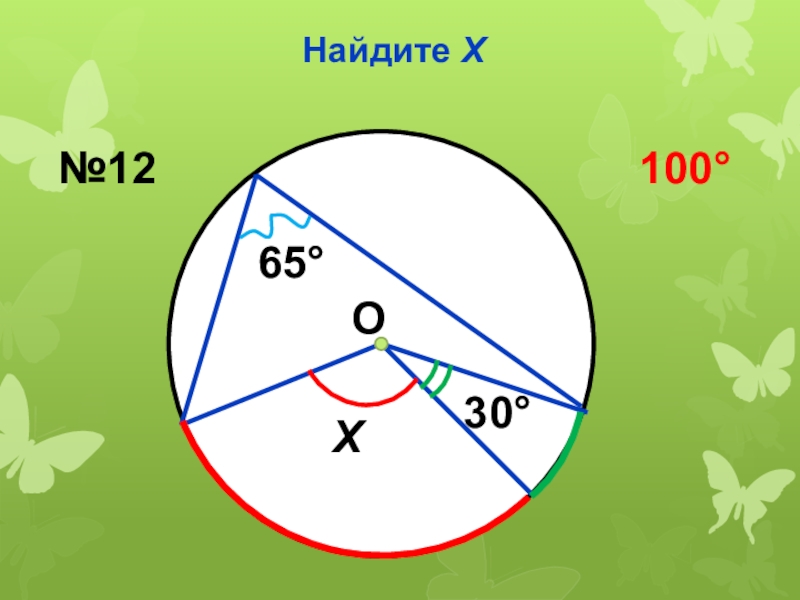
- 33. Найдите Х3065Х№12100О
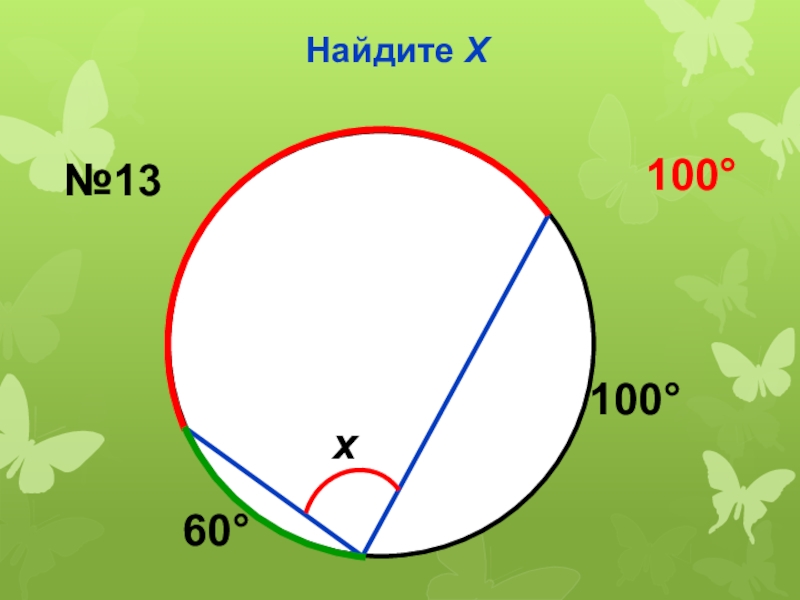
- 34. Найдите Х60100x№13100
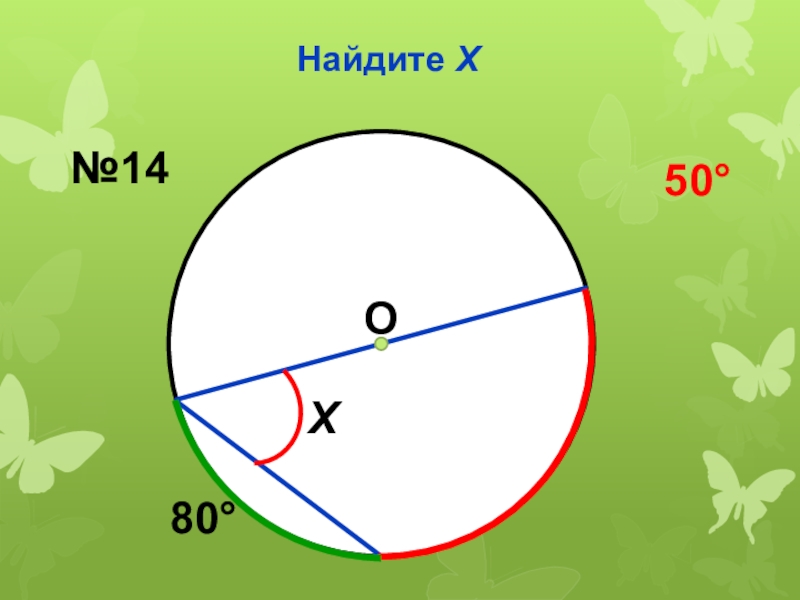
- 35. Найдите ХО80Х№1450
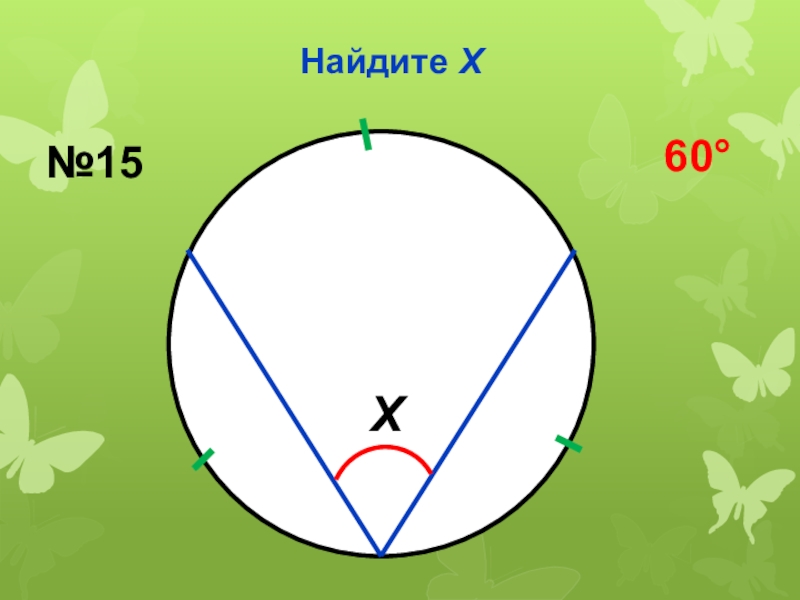
- 36. Найдите ХХ№1560
- 37. Найдите Хx№1636
- 38. Найдите ХОХ№1790
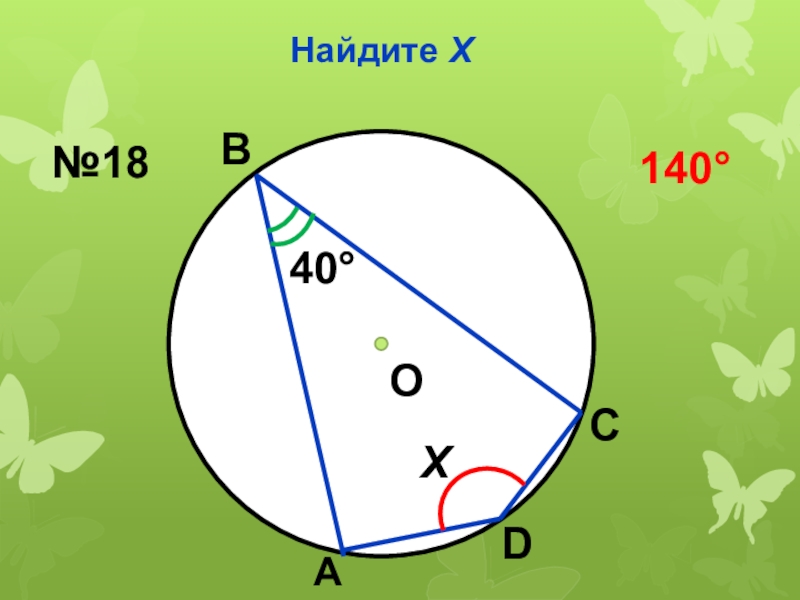
- 39. Найдите ХО40ХВАСD№18140
- 40. Найдите ХО110ХАСВ№19125
- 41. Найдите ХО100ХАВС№20160
- 42. Найдите ХО30Х№2130АВСD
- 43. Найдите ХО30ХАСвD№22120
- 44. Найдите ХО35ХАСВD№2355
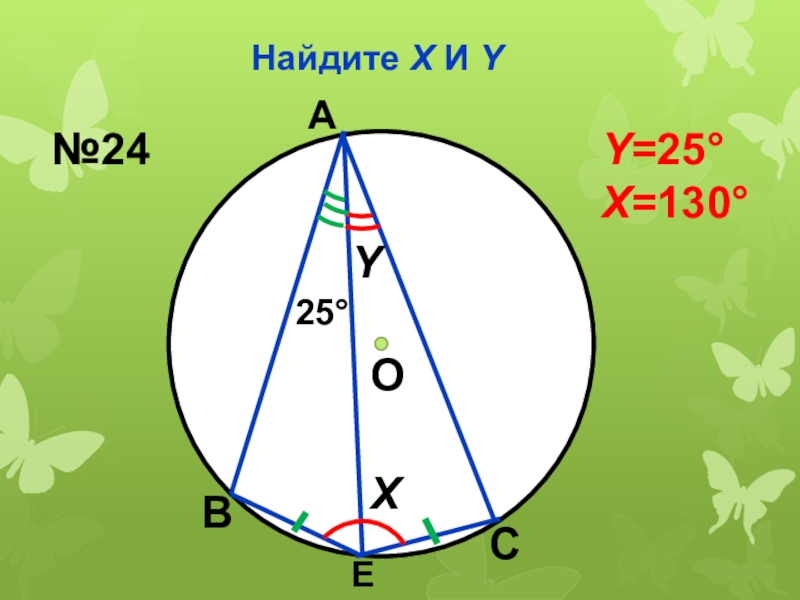
- 45. Найдите Х И YОХY25АВСЕ№24Y=25Х=130
- 46. Найдите ХХО40АDВС№2550
- 47. Найдите ХВКАDОСХ5020№2660
- 48. Домашнее задание: П. 70-73 изучить и выучить.№
- 49. Скачать презентанцию
Слайды и текст этой презентации
Слайд 4О
Сначала вспомним как задаётся окружность
Окружность (О, r)
r – радиус
r
A
B
АВ –
хорда
С
D
CD - диаметр
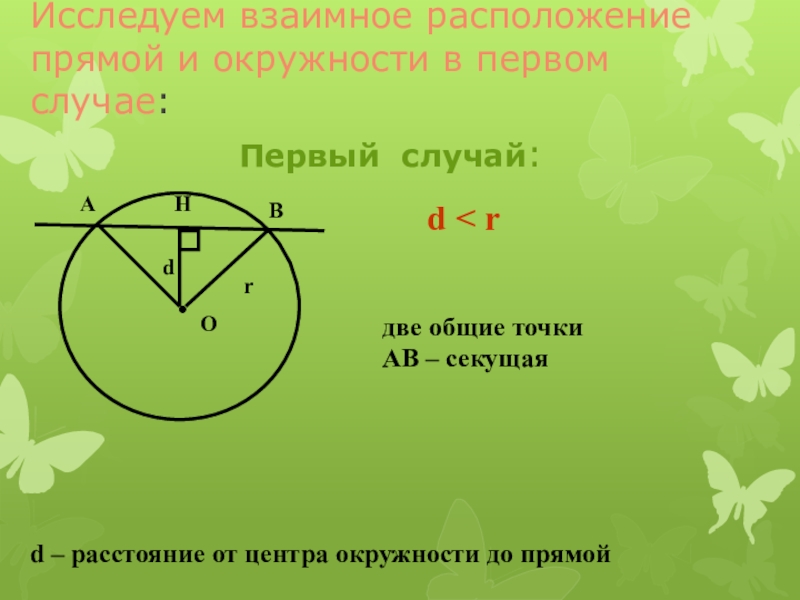
Слайд 5Исследуем взаимное расположение прямой и окружности в первом случае:
d –
расстояние от центра окружности до прямой
О
А
В
Н
d < r
две общие точки
АВ
– секущая r
d
Первый случай:
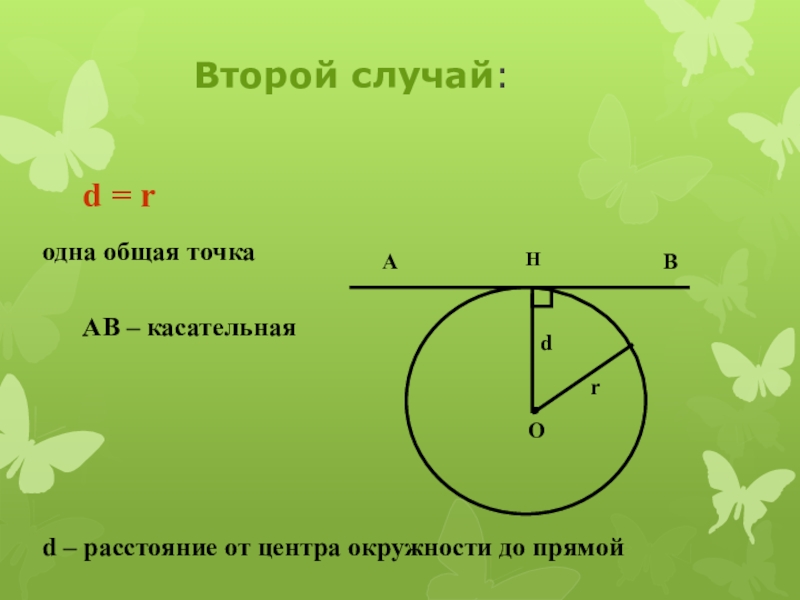
Слайд 6Второй случай:
О
Н
r
одна общая точка
d = r
d – расстояние от центра
окружности до прямой
d
А
В
АВ – касательная
Слайд 8Сколько общих точек могут иметь прямая и окружность?
d
r
d = r
d > r
две общие точки
одна общая точка
не имеют
общих точекЕсли расстояние от центра окружности до прямой меньше радиуса окружности, то прямая и окружность имеют две общие точки.
Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая и окружность имеют только одну общую точку.
Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общих точек.
Слайд 9Касательная к окружности
Определение: Прямая, имеющая с окружностью только одну общую
точку, называется касательной к окружности, а их общая точка называется
точкой касания прямой и окружности.O
s=r
M
m
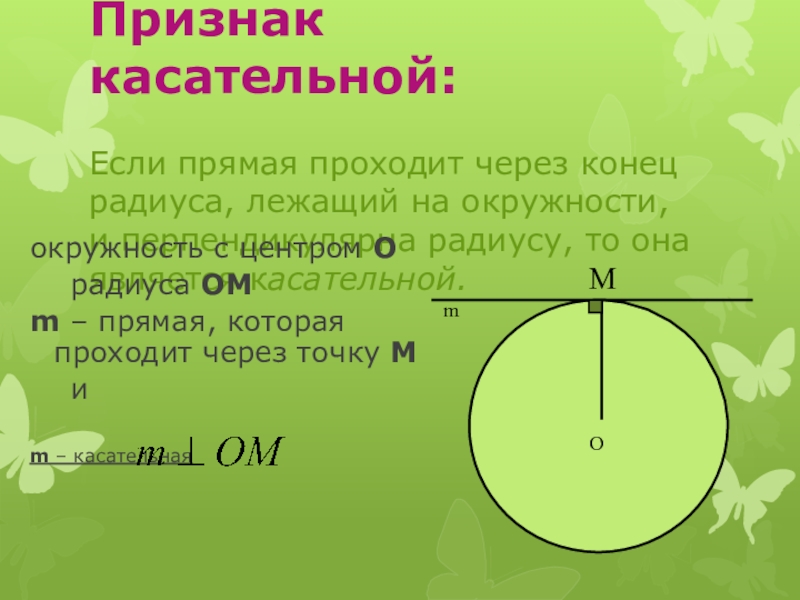
Слайд 11Признак касательной: Если прямая проходит через конец радиуса, лежащий на окружности,
и перпендикулярна радиусу, то она является касательной.
окружность с центром О
радиуса OMm – прямая, которая проходит через точку М
и
m – касательная
O
M
m
Слайд 15А
О
С
B
К
4,5
?
1. Рассмотрим -ки АОВ и АОС
- равны(?) →
2.
3.
4. ОВ =4,5 ОА=9
→ (?)5.
BАО=
САО
BАО и
BАО - прямоугольные (?)
BАС= 60
Слайд 18Дуга окружности, соответствующая центральному углу
это часть окружности, расположенная внутри угла
Градусная
мера дуги окружности
равна градусной мере соответствующего центрального угла.
А
В
АВ
= АОВ
О
Слайд 19Вписанный угол
Это угол, вершина которого лежит на окружности, а стороны
пересекают окружность.
С
А
В
Слайд 20Теорема о вписанном угле
Угол, вписанный в окружность, равен половине соответствующего
ему центрального угла.
Угол, вписанный в окружность, равен половине дуги, на
которую он опирается.С
А
В
О
Слайд 48Домашнее задание:
П. 70-73 изучить и выучить.
№ 631( а,б), 638,642,647 (в)
(эти номера сдать до четверга)
№ 649( а), 650(б), 652, 653
(а,б) ,654, 656( сдать до субботы)Не делайте всё вместе!!!