Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тема 10. Алгоритмы на графах
Содержание
- 1. Тема 10. Алгоритмы на графах
- 2. Программирование и основы алгоритмизацииТема 10. Алгоритмы на
- 3. Cij Программирование и основы алгоритмизацииТема 10. Алгоритмы
- 4. Программирование и основы алгоритмизацииТема 10. Алгоритмы на
- 5. Программирование и основы алгоритмизацииТема 10. Алгоритмы на
- 6. Программирование и основы алгоритмизацииТема 10. Алгоритмы на
- 7. Программирование и основы алгоритмизацииТема 10. Алгоритмы на
- 8. Программирование и основы алгоритмизацииТема 10. Алгоритмы на
- 9. Программирование и основы алгоритмизацииТема 10. Алгоритмы на графах9Шевченко А. В.Алгоритм УоршаллаCij 1234561112113141151671871811Tij ......
- 10. Программирование и основы алгоритмизацииТема 10. Алгоритмы на графах10Шевченко А. В.Алгоритм УоршаллаTij 123456111111211111314111115111116711118117111181111111
- 11. Программирование и основы алгоритмизацииТема 10. Алгоритмы на
- 12. Программирование и основы алгоритмизацииТема 10. Алгоритмы на
- 13. Программирование и основы алгоритмизацииТема 10. Алгоритмы на
- 14. Программирование и основы алгоритмизацииТема 10. Алгоритмы на
- 15. Программирование и основы алгоритмизацииТема 10. Алгоритмы на
- 16. Программирование и основы алгоритмизацииТема 10. Алгоритмы на
- 17. Программирование и основы алгоритмизацииТема 10. Алгоритмы на
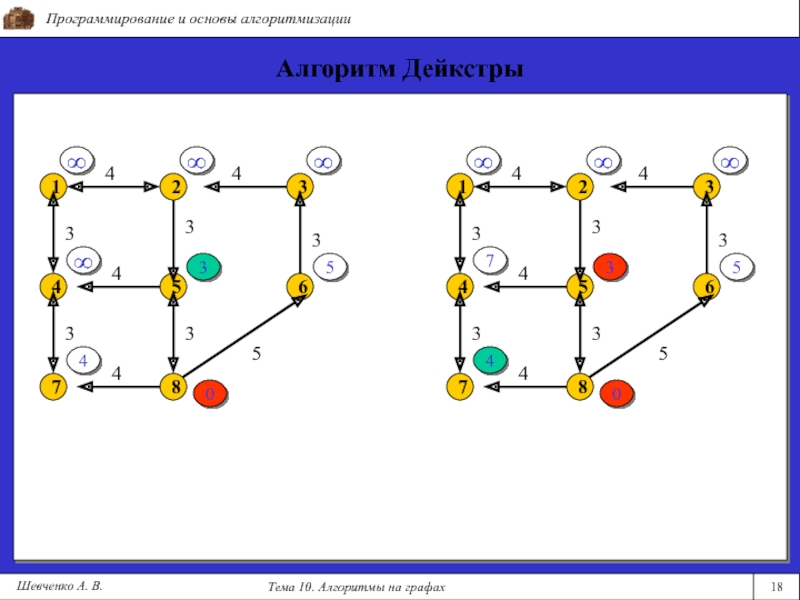
- 18. Программирование и основы алгоритмизацииТема 10. Алгоритмы на графах18Шевченко А. В.Алгоритм Дейкстры354035740
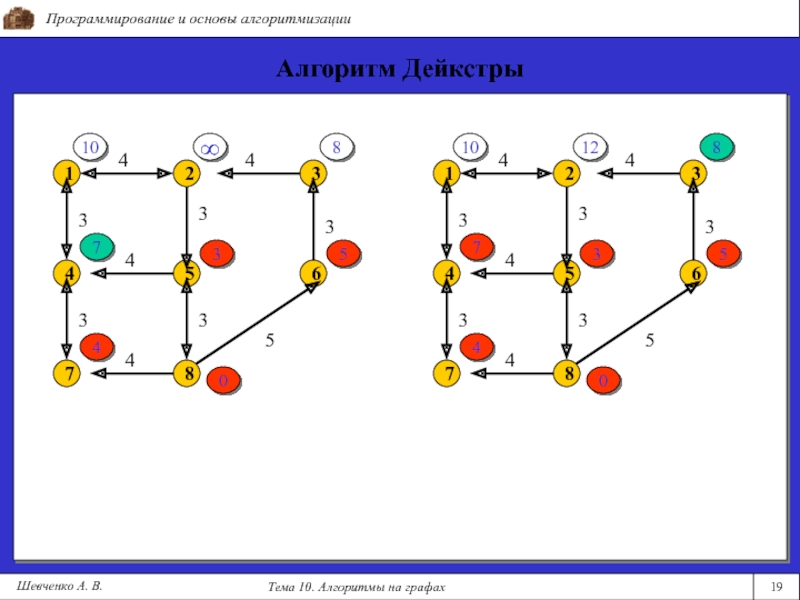
- 19. Программирование и основы алгоритмизацииТема 10. Алгоритмы на графах19Шевченко А. В.Алгоритм Дейкстры108357401012835740
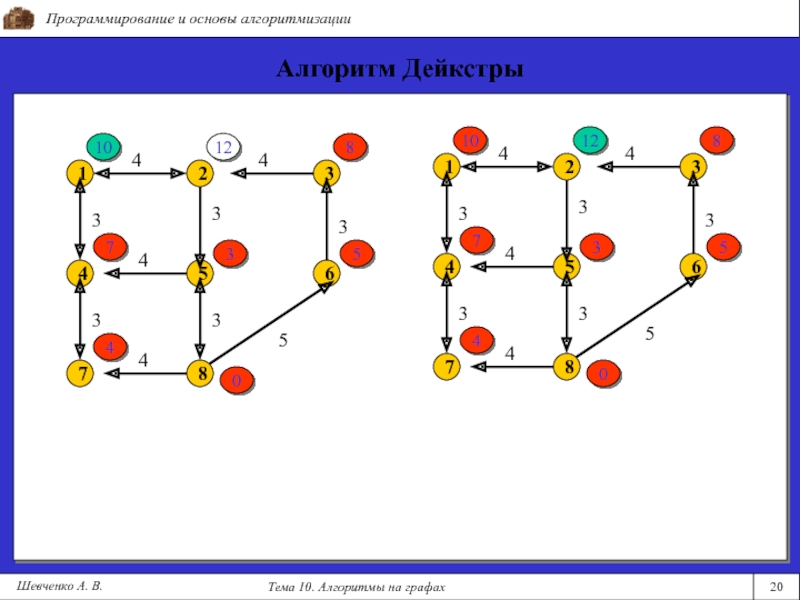
- 20. Программирование и основы алгоритмизацииТема 10. Алгоритмы на графах20Шевченко А. В.Алгоритм Дейкстры10128357401012835740
- 21. Скачать презентанцию
Программирование и основы алгоритмизацииТема 10. Алгоритмы на графах2Шевченко А. В.Задачи на связностьПример 1. Контроль качества печатных платВ процессе изготовления печатных плат металлизированные отверстия соединяются проводниками. При контроле продукции проверяется наличие или
Слайды и текст этой презентации
Слайд 1Программирование и основы алгоритмизации
Тема 10. Алгоритмы на графах
1
Тема 10. Алгоритмы
на графах
Слайд 2Программирование и основы алгоритмизации
Тема 10. Алгоритмы на графах
2
Шевченко А. В.
Задачи
на связность
Пример 1. Контроль качества печатных плат
В процессе изготовления печатных
плат металлизированные отверстия соединяются проводниками. При контроле продукции проверяется наличие или отсутствие соединения между различными точками.Слайд 3Cij
Программирование и основы алгоритмизации
Тема 10. Алгоритмы на графах
3
Шевченко А.
В.
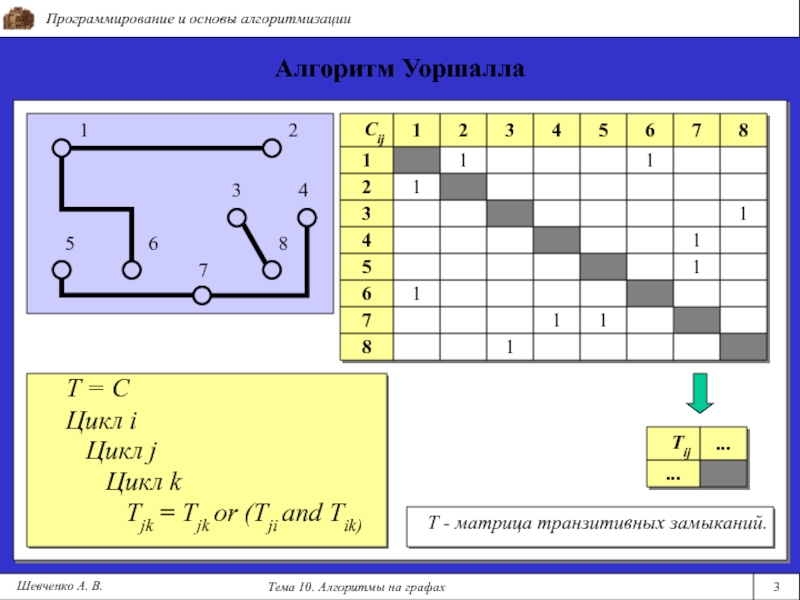
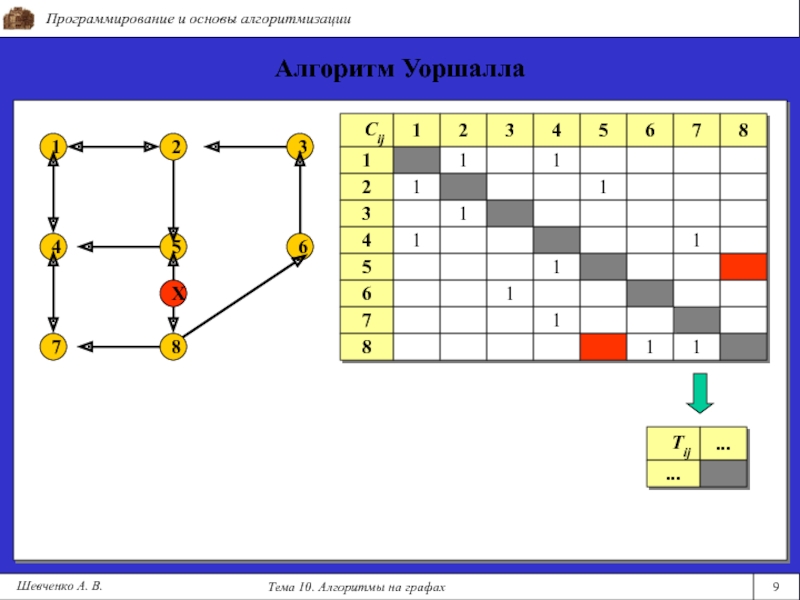
Алгоритм Уоршалла
1
2
3
4
5
6
1
1
1
2
1
3
4
5
6
1
1
2
3
4
5
6
7
8
7
1
8
1
1
7
1
1
8
1
T = C
Цикл i
Цикл j
Цикл kTjk = Tjk or (Tji and Tik)
Tij
...
...
Т - матрица транзитивных замыканий.
Слайд 4Программирование и основы алгоритмизации
Тема 10. Алгоритмы на графах
4
Шевченко А. В.
Алгоритм
Уоршалла
int C[8][8] = {{-1, 1, 0, 0, 0, 1, 0,
0}, ...};int T[8][8];
int n = 8;
for(int i = 0; i < n; i++)
for(int j = 0; j < n; j++)
T[i][j] = C[i][j];
for(int i = 0; i < n; i++)
for(int j = 0; j < n; j++)
if(j != i)
for(int k = 0; k < n; k++)
if(k != j)
T[j][k] = T[j][k] || T[j][i] && T[i][k];
Слайд 5Программирование и основы алгоритмизации
Тема 10. Алгоритмы на графах
5
Шевченко А. В.
Алгоритм
Уоршалла
Tij
1
2
3
4
5
6
1
1
1
2
1
1
3
4
1
5
1
6
1
1
1
2
3
4
5
6
7
8
7
1
8
1
1
7
1
1
8
1
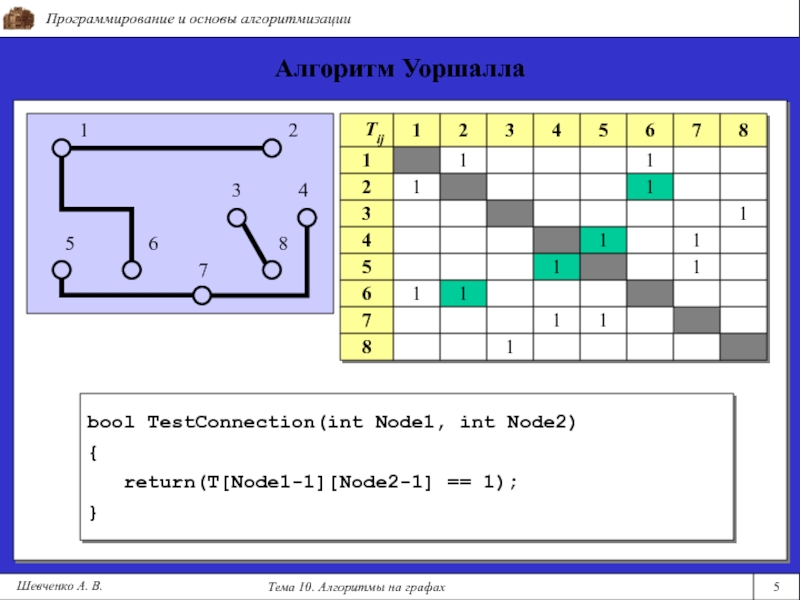
bool TestConnection(int Node1, int Node2)
{
return(T[Node1-1][Node2-1] == 1);
}
Слайд 6Программирование и основы алгоритмизации
Тема 10. Алгоритмы на графах
6
Шевченко А. В.
Задачи
на связность
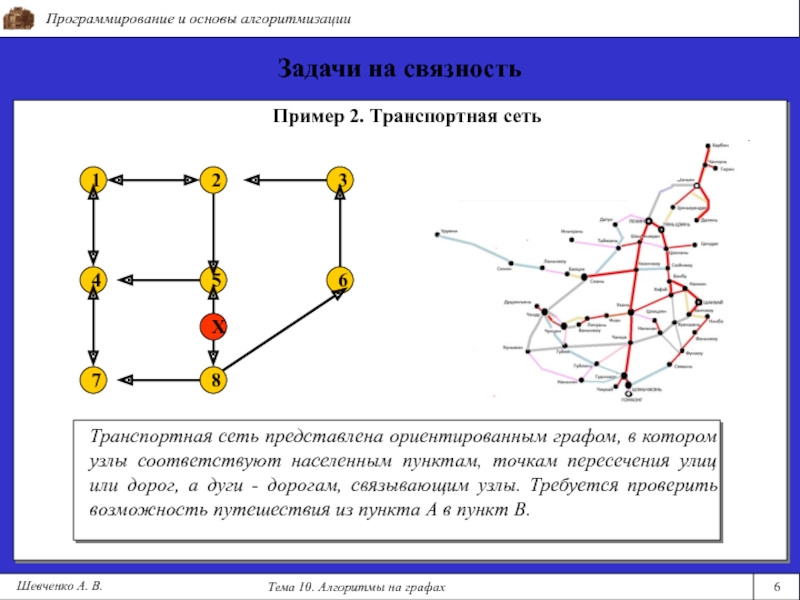
Пример 2. Транспортная сеть
Транспортная сеть представлена ориентированным графом, в
котором узлы соответствуют населенным пунктам, точкам пересечения улиц или дорог, а дуги - дорогам, связывающим узлы. Требуется проверить возможность путешествия из пункта А в пункт В.Слайд 7Программирование и основы алгоритмизации
Тема 10. Алгоритмы на графах
7
Шевченко А. В.
Алгоритм
Уоршалла
Cij
1
2
3
4
5
6
1
1
1
2
1
1
3
1
4
1
1
5
1
6
7
1
8
1
7
1
8
1
1
1
Tij
...
...
1
3
2
5
4
6
7
8
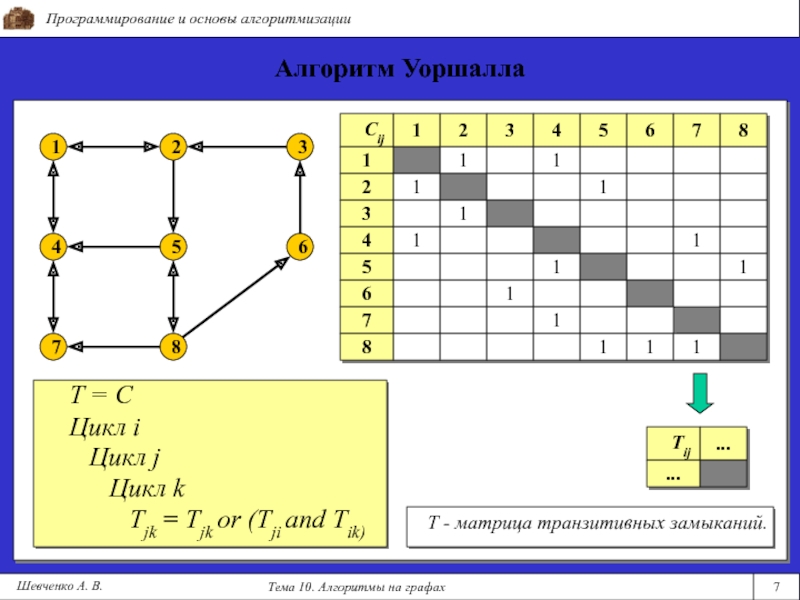
T = C
Цикл i
Цикл j
Цикл kTjk = Tjk or (Tji and Tik)
Т - матрица транзитивных замыканий.
Слайд 8Программирование и основы алгоритмизации
Тема 10. Алгоритмы на графах
7
Шевченко А. В.
Алгоритм
Уоршалла
Tij
1
2
3
4
5
6
1
1
1
1
1
1
2
1
1
1
1
1
3
1
1
1
1
1
4
1
1
1
1
1
5
1
1
1
1
1
6
1
1
1
1
1
7
1
1
1
1
8
1
1
1
1
1
1
1
1
7
1
1
1
1
1
8
1
1
1
1
1
1
1
1
1
1
3
2
5
4
6
7
8
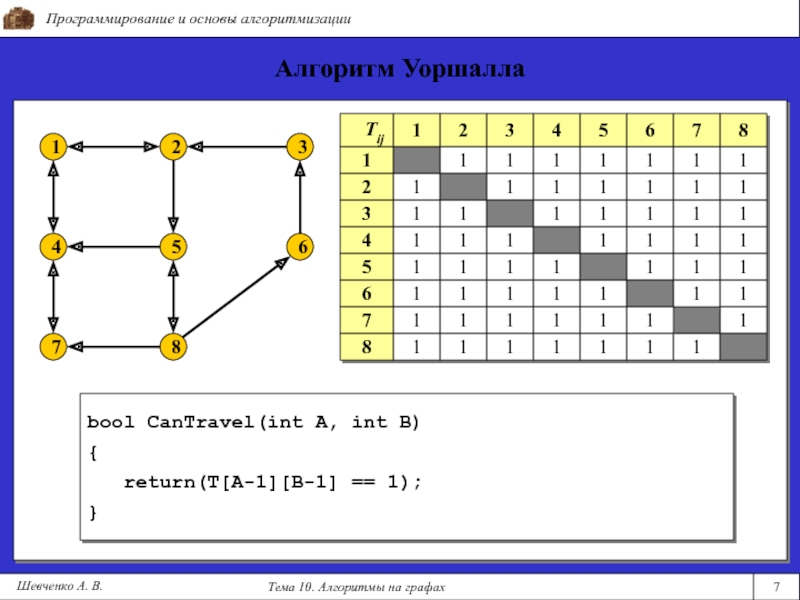
bool CanTravel(int A, int B)
{
return(T[A-1][B-1] == 1);
}
Слайд 9Программирование и основы алгоритмизации
Тема 10. Алгоритмы на графах
9
Шевченко А. В.
Алгоритм
Уоршалла
Cij
1
2
3
4
5
6
1
1
1
2
1
1
3
1
4
1
1
5
1
6
7
1
8
7
1
8
1
1
Tij
...
...
Слайд 10Программирование и основы алгоритмизации
Тема 10. Алгоритмы на графах
10
Шевченко А. В.
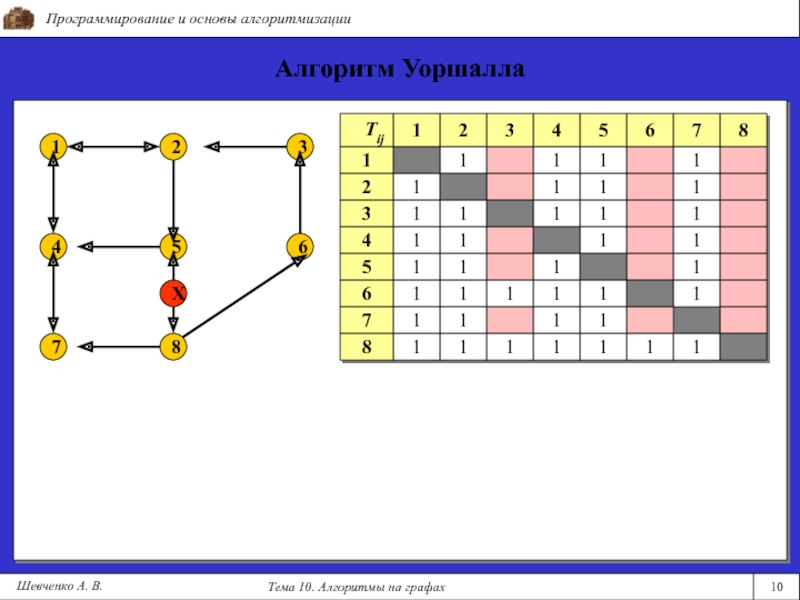
Алгоритм
Уоршалла
Tij
1
2
3
4
5
6
1
1
1
1
1
1
2
1
1
1
1
1
3
1
4
1
1
1
1
1
5
1
1
1
1
1
6
7
1
1
1
1
8
1
1
7
1
1
1
1
8
1
1
1
1
1
1
1
Слайд 11Программирование и основы алгоритмизации
Тема 10. Алгоритмы на графах
11
Шевченко А. В.
Задачи
на поиск минимального пути
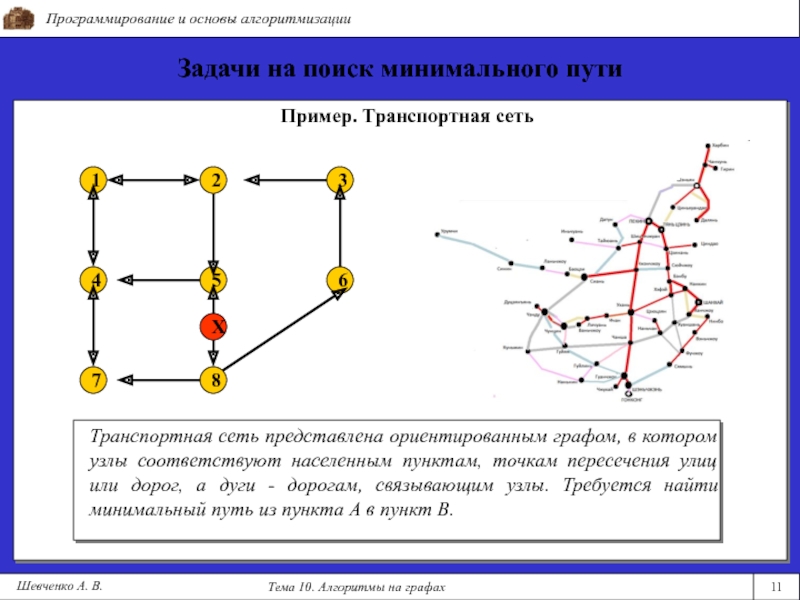
Пример. Транспортная сеть
Транспортная сеть представлена ориентированным графом,
в котором узлы соответствуют населенным пунктам, точкам пересечения улиц или дорог, а дуги - дорогам, связывающим узлы. Требуется найти минимальный путь из пункта А в пункт В.Слайд 12Программирование и основы алгоритмизации
Тема 10. Алгоритмы на графах
12
Шевченко А. В.
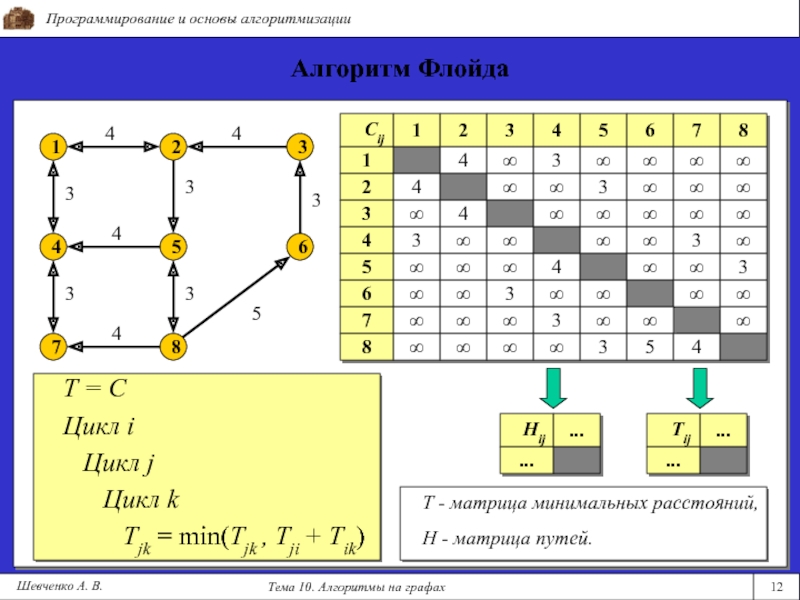
Алгоритм
Флойда
Сij
1
2
3
4
5
6
1
4
3
2
4
4
3
3
4
3
4
5
3
6
7
3
8
3
7
3
8
3
5
4
1
3
2
5
4
6
7
8
4
4
4
4
3
3
3
3
3
5
Tij
...
...
Hij
...
...
T = C
Цикл i
Цикл j
Цикл kTjk = min(Tjk , Tji + Tik)
Т - матрица минимальных расстояний,
Н - матрица путей.
Слайд 13Программирование и основы алгоритмизации
Тема 10. Алгоритмы на графах
13
Шевченко А. В.
Алгоритм
Флойда
const int INF 1000000
int C[8][8] = {{INF, 4, INF, 3,
INF, INF, INF, INF}, ...};int T[8][8];
int H[8][8];
const int n = 8;
for(int i = 0; i < n; i++)
for(int j = 0; j < n; j++)
{
T[i][j] = C[i][j];
if(C[i][j] == INF)
H[i][j] = -1;
else
H[i][j] = j;
}
Слайд 14Программирование и основы алгоритмизации
Тема 10. Алгоритмы на графах
14
Шевченко А. В.
Алгоритм
Флойда
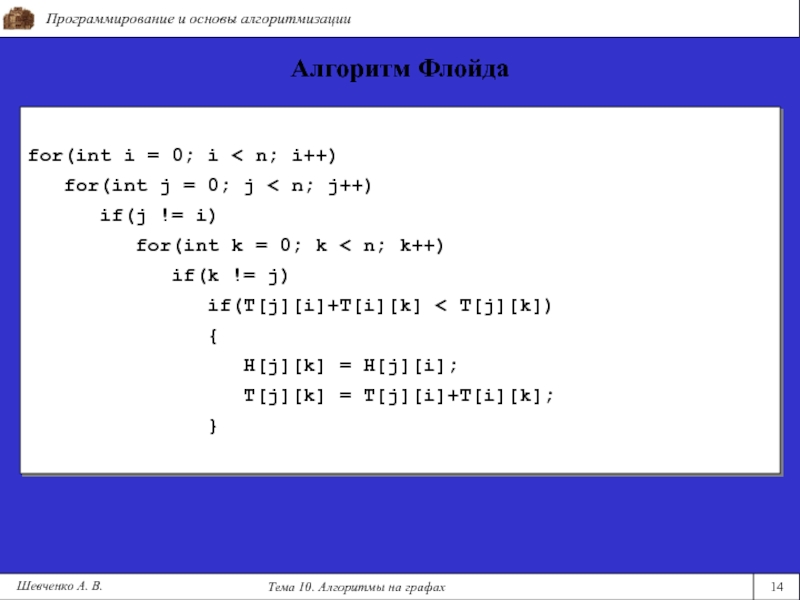
for(int i = 0; i < n; i++)
for(int
j = 0; j < n; j++)if(j != i)
for(int k = 0; k < n; k++)
if(k != j)
if(T[j][i]+T[i][k] < T[j][k])
{
H[j][k] = H[j][i];
T[j][k] = T[j][i]+T[i][k];
}
Слайд 15Программирование и основы алгоритмизации
Тема 10. Алгоритмы на графах
15
Шевченко А. В.
Алгоритм
Флойда
1
3
2
5
4
6
7
8
4
4
4
4
3
3
3
3
3
5
Hij
1
2
3
4
5
6
1
2
2
4
4
2
2
1
3
1
1
3
3
6
6
6
6
6
4
1
5
5
5
5
5
2
2
2
2
2
6
8
8
8
8
8
7
4
8
8
4
8
5
5
5
5
8
8
5
5
7
4
1
6
7
2
8
4
3
6
7
8
8
8
8
5
Tij
1
2
3
4
5
6
1
4
8
3
7
11
2
4
4
7
11
7
3
18
14
21
11
3
4
3
7
11
4
14
5
7
3
7
10
10
6
15
11
15
18
8
7
6
10
14
3
8
10
6
10
13
7
17
3
13
7
6
10
24
3
13
8
10
12
8
7
3
21
5
4
16
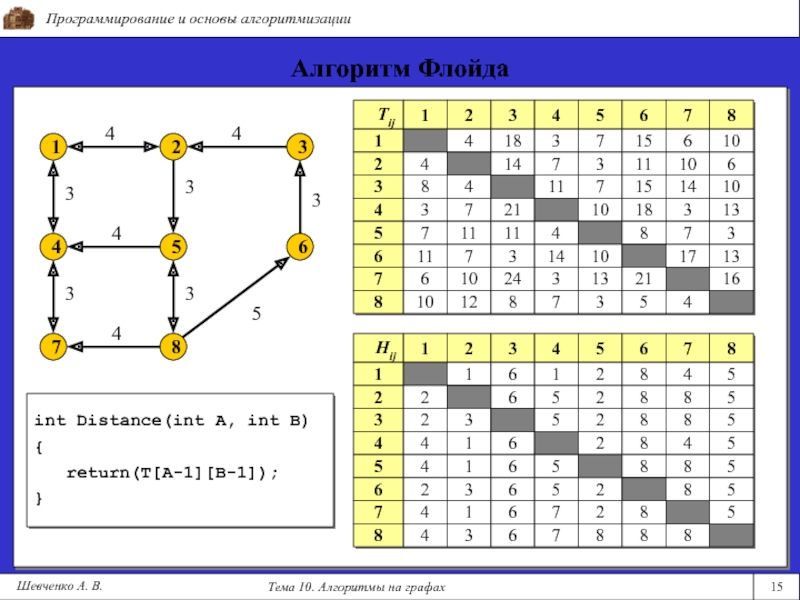
int Distance(int A, int B)
{
return(T[A-1][B-1]);
}
Слайд 16Программирование и основы алгоритмизации
Тема 10. Алгоритмы на графах
16
Шевченко А. В.
Алгоритм
Флойда
1
3
2
5
4
6
7
8
4
4
4
4
3
3
3
3
3
5
Hij
1
2
3
4
5
6
1
2
2
4
4
2
2
1
3
1
1
3
3
6
6
6
6
6
4
1
5
5
5
5
5
2
2
2
2
2
6
8
8
8
8
8
7
4
8
8
4
8
5
5
5
5
8
8
5
5
7
4
1
6
7
2
8
4
3
6
7
8
8
8
8
5
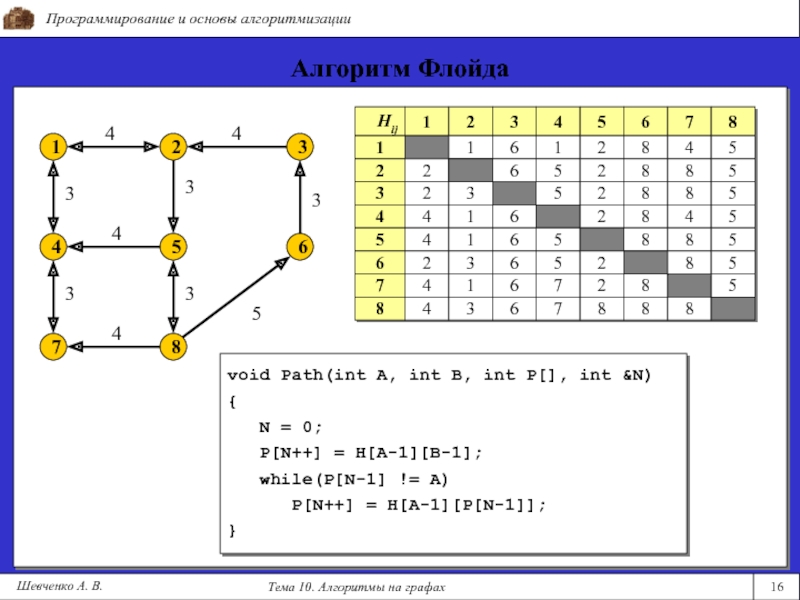
void Path(int A, int B, int P[], int &N)
{
N = 0;P[N++] = H[A-1][B-1];
while(P[N-1] != A)
P[N++] = H[A-1][P[N-1]];
}
Слайд 17Программирование и основы алгоритмизации
Тема 10. Алгоритмы на графах
17
Шевченко А. В.
Алгоритм
Дейкстры
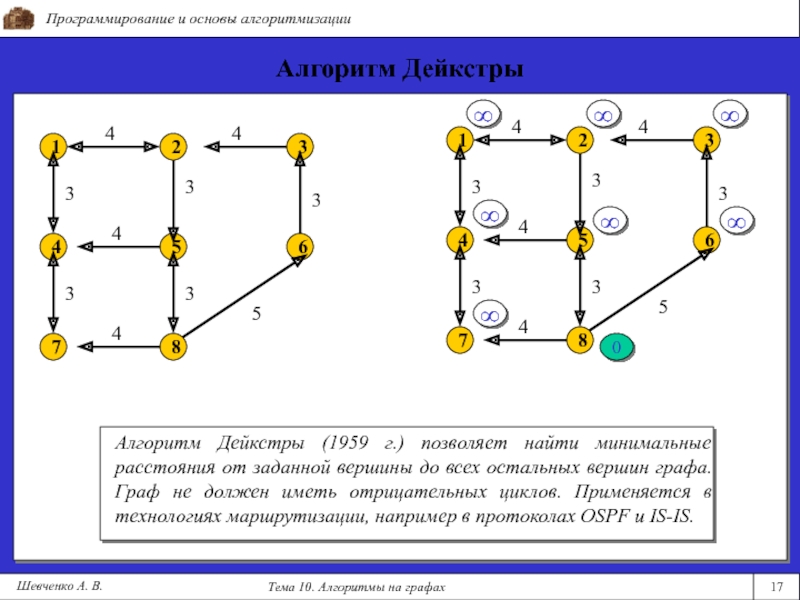
Алгоритм Дейкстры (1959 г.) позволяет найти минимальные расстояния от заданной
вершины до всех остальных вершин графа. Граф не должен иметь отрицательных циклов. Применяется в технологиях маршрутизации, например в протоколах OSPF и IS-IS.
0


![Тема 10. Алгоритмы на графах Программирование и основы алгоритмизацииТема 10. Алгоритмы на графах4Шевченко А. В.Алгоритм Уоршаллаint Программирование и основы алгоритмизацииТема 10. Алгоритмы на графах4Шевченко А. В.Алгоритм Уоршаллаint C[8][8] = {{-1, 1, 0, 0,](/img/thumbs/551c6e10afcc4f34adae56c6818c8ece-800x.jpg)
![Тема 10. Алгоритмы на графах Программирование и основы алгоритмизацииТема 10. Алгоритмы на графах13Шевченко А. В.Алгоритм Флойдаconst Программирование и основы алгоритмизацииТема 10. Алгоритмы на графах13Шевченко А. В.Алгоритм Флойдаconst int INF 1000000int C[8][8] = {{INF,](/img/thumbs/a87b72bdd170d7e95e3ab00a804de99b-800x.jpg)