Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тема 2. ФИНАНСОВЫЕ ВЫЧИСЛЕНИЯ В УПРАВЛЕНИИ ИНВЕСТИЦИОННО-СТРОИТЕЛЬНЫМИ
Содержание
- 1. Тема 2. ФИНАНСОВЫЕ ВЫЧИСЛЕНИЯ В УПРАВЛЕНИИ ИНВЕСТИЦИОННО-СТРОИТЕЛЬНЫМИ
- 2. Литература:Цены и ценообразование. 5-е изд.- СПб.: Питер,
- 3. Основные причины изменения стоимости денег во времени
- 4. СТОИМОСТЬ ДЕНЕГ ВО ВРЕМЕНИНормально функционирующая экономика предполагает,
- 5. Простой процент - это начисление процента только
- 6. Сложный процент - это процент, начисляемый на
- 7. Пример расчета по простому и сложному проценту(сумма
- 8. ЭФФЕКТИВНАЯ И НОМИНАЛЬНАЯ СТАВКА ПРОЦЕНТАВ различных финансовых
- 9. Обратная задача, когда известна сумма, которая будет
- 10. Пример №1: Требуется оценить стоимость инвестиционно-строительного проекта
- 11. РЕШЕНИЕ
- 12. Если гарантируется постоянный доход в течение бесконечного
- 13. Пример №2: Требуется определить величину инвестиций в
- 14. БЕСКОНЕЧНЫЙ ПОТОК УВЕЛИЧИВАЮЩИХСЯ ПЛАТЕЖЕЙПредположим, что в предыдущей
- 15. Пример №3: Требуется определить величину вклада на
- 16. Стандартные функции сложного процента для расчета денежных
- 17. РЕШЕНИЕ
- 18. Понятие «АННУИТЕТ»Аннуитетом (аnnuity) или финансовой рентой называют
- 19. Настоящая стоимость аннуитета (пс)- функция, определяющая настоящую
- 20. РЕШЕНИЕЕсли в условии было бы сказано, что
- 21. Будущая стоимость единицы (amount of I at
- 22. РЕШЕНИЕ
- 23. Будущая стоимость аннуитета (БС) — показывает, какова
- 24. РЕШЕНИЕ
- 25. Фактор фонда возмещения (плт) — величина платежа
- 26. РЕШЕНИЕСумма, которую надо будет откладывать собственнику равна 1000х0,0164=16,4
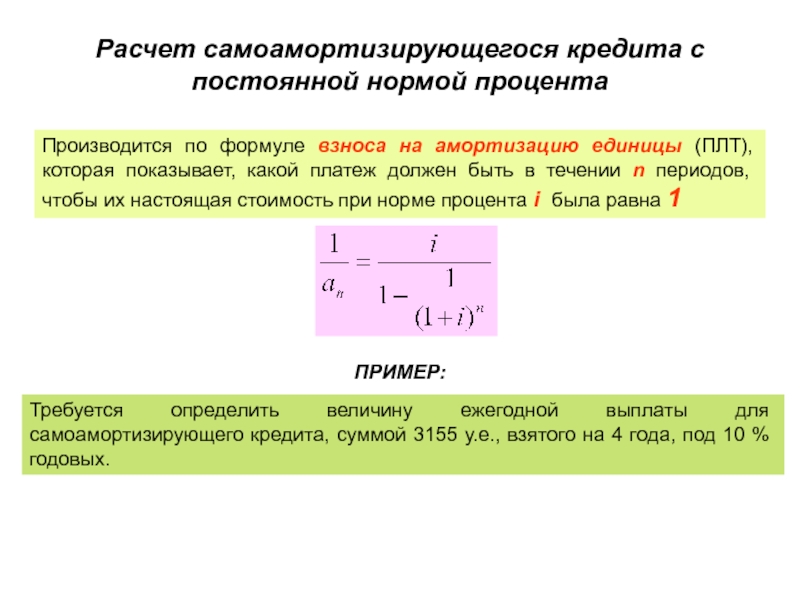
- 27. Расчет самоамортизирующегося кредита с постоянной нормой процентаПроизводится
- 28. РЕШЕНИЕТогда платеж по кредиту будет 3155х0,3155=1000
- 29. ВЗАИМОСВЯЗЬ МЕЖДУ ШЕСТЬЮ ФУНКЦИЯМИ СЛОЖНОГО ПРОЦЕНТА
- 30. ДОПОЛНИТЕЛЬНЫЕ ФУНКЦИИ1. Количество периодов. Для определения количества
- 31. РЕШЕНИЕ №1КПЕР (ставка; плата; пс; бс; тип)= (10%;-1000;;16000;0)=10 .РЕШЕНИЕ №2КПЕР (ставка; плата; пс; бс; тип)= (10%;;-10000;20000;0)=7,3
- 32. Норма. Для определения i - нормы (ставки,
- 33. РЕШЕНИЕ №1СТАВКА (кпер; плт; пс, бс; тип)=
- 34. Текущая стоимость неравномерного потока. Функция ЧПС (ставка;
- 35. РЕШЕНИЕСоздаем массив положительных денежных потоков:в момент времени
- 36. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Тема 2. ФИНАНСОВЫЕ ВЫЧИСЛЕНИЯ В УПРАВЛЕНИИ ИНВЕСТИЦИОННО-СТРОИТЕЛЬНЫМИ ПРОЕКТАМИ
Учет стоимости денег
во времени при управлении ИСП
процента для расчета денежных потоков при Управлении ИСПСлайд 2Литература:
Цены и ценообразование. 5-е изд.- СПб.: Питер, 2007.- 560 с.:
ил.- (Серия «Учебник для вузов»).
Валдайцев С.В. Оценка бизнеса: учеб.- 3-е
изд., перераб. и доп. М.: ТК Велби, Изд-во Проспект, 2008, 576 с.Валдайцев, В.С. Оценка бизнеса и инноваций: Учебное пособие для студентов и преподавателей. / В.С. Валдайцев. – М.: Филинъ, 2015. – 486 с.
Григорьев, В.В. Оценка предприятия: теория и практика. / В.В. Григорьев. – М.: НОРМА-ИНФРА-М, 2014. – 320 с.
Есипов, В.E. Оценка бизнеса: учебник /В.Е. Есипов. – 2-е изд. – СПб.: Питер, 2015. – 464 с.
5. Оценка бизнеса: Учебник / А.Г. Грязнова, М.А. Федотова. – М.: «Финансы и статистика», 2014. – 387 с.
Рутгайзер В.М. Оценка стоимости бизнеса. Учебное пособие. – М.: Инфра-М, 2015. – 312с.
Щербаков, В.А. Оценка стоимости предприятия (бизнеса). / В.А. Щербаков. – М.: Издательство Омега, 2014. – 288 с.
Слайд 3Основные причины изменения стоимости денег во времени
При
вложении средств (приобретении прав владения строительным бизнесом) инвестор отказывается от
текущего потребления в надежде получить больший доход в будущем. Однако существует риск неполучения ожидаемого дохода. Поэтому инвестор заслуживает премии, что является ключевым фактором необходимости учета стоимости денег во времени при управлении ИСП.Основные причины изменения стоимости денег во времени:
1. Инвестор отказывается от текущего потребления, за что заслуживает премии.
2. Инвестор берет на себя риск неполучения ожидаемого до
хода, что требует учета премии за риск, связанный с объектом
инвестирования.
3. Меняется покупательная способность денег.
Слайд 4СТОИМОСТЬ ДЕНЕГ ВО ВРЕМЕНИ
Нормально функционирующая экономика предполагает, что только за
определенную плату сегодня можно взять (или дать) деньги в пользование
на определенный срок (n - число периодов в месяцах, кварталах, годах), рассчитывая получить за это вознаграждение (i - норма процента, стоимость денег во времени, норма прибыли).Условно принято различать схему начисления процентов на простую и сложную. Когда деньги инвестируются под сложный процент, то каждый процентный платеж реинвестируется, регулярно увеличивая базу начисления процента для следующего периода. При инвестировании денег под простой процент процентные платежи регулярно начисляются исходя из суммы первоначально вклада.
Разница при расчетах с применением простого и сложного процента становится тем существеннее, чем дольше период поступления платежей.
При решении различных финансовых задач рыночной экономики, в том числе управлении инвестиционно-строительными проектами принято оперировать понятием сложного процента. Остаток на счете при начислении сложных процентов можно вычислить по формуле:
PV – сумма, которую инвестор имеет сегодня (стоимость на настоящее время) - FV сумма которую инвестор получит через n лет при ставке процента - i , которую принято называть нормой оплаты за пользование капиталом.
Слайд 5Простой процент - это начисление процента только на первоначально инвестированную
сумму (принципал).
Например, в начале периода (года) инвестируется сумма Р
под простой процент r. В конце первого периода инвестор получит:В конце второго периода:
В конце n-го периода:
Более подробно о вычислениях по простому и сложному проценту
Слайд 6Сложный процент - это процент, начисляемый на сложную базу, включающую
первоначально инвестируемую сумму (принципал) и ранее начисленные проценты.
Например, в начале
периода (года) инвестируется сумма Р под простой процент r. В конце первого периода инвестор получит:В конце второго периода:
В конце n-го периода:
Слайд 7Пример расчета по простому и сложному проценту
(сумма 100 тыс. руб.,
период – 4 года, ставка – 10%)
Слайд 8ЭФФЕКТИВНАЯ И НОМИНАЛЬНАЯ СТАВКА ПРОЦЕНТА
В различных финансовых операциях могут использоваться
разные схемы начисления процентов. Как правило, заранее оговаривается номинальная процентная
ставка и схема ее начисления. Однако номинальная процентная ставка не отражает действительной эффективности финансовой операции и не может быть использована для сравнений. Для сравнительного анализа необходим показатель, который был бы универсальным при любой схеме начисления процентов. Таким показателем является эффективная процентная ставка (re). Под эффективной процентной ставкой понимают годовую процентную ставку, связывающую сегодняшнюю и будущую ценность платежа или потока платежей.Пример:
Банк начисляет 10% годовых один раз в полугодие. 10% - это номинальная процентная ставка. Эффективная процентная ставка определяется следующим образом.
Слайд 9Обратная задача, когда известна сумма, которая будет получена через n
– периодов, а определяем, какую сумму следует сегодня инвестировать, если
норма оплаты за пользование капиталом равна i ?PV – сегодняшняя ценность будущих доходов - FV , полученных через n лет при ставке процента (дисконта, капитализации) - i .
Сегодняшний доллар эквивалентен завтрашнему доллару умноженному на коэффициент дисконта (или коэффициент уменьшения – аn)
Еcли денежные потоки (платежи по периодам) неодинаковы то выражение для определения настоящей стоимости денежных потоков примет вид:
Это выражение называется формулой дисконтированного денежного потока
Слайд 10Пример №1:
Требуется оценить стоимость инвестиционно-строительного проекта по приносимому им доходу,
если известно, что доход за три года эксплуатации построенного объекта
(срок службы с 2019 по 2021 г.г.) составит 800, 500 и 300 тыс. руб. за первый, второй и третий годы соответственно. При этом рыночная ставка процента (дисконтирования, капитализации) может составить 10%.Слайд 12Если гарантируется постоянный доход в течение бесконечного числа периодов (например
бессрочные облигации), то ряд дисконтированного потока будет выглядеть так:
Полученное
выражение определяет настоящую стоимость бесконечного потока равномерных постоянных платежей при норме дисконта, равной iСлайд 13Пример №2:
Требуется определить величину инвестиций в строительный проект, который обеспечивал
бы ежегодное получение 5 млн. руб. в виде процентных платежей
в течение бесконечного периода времени. Величина премии за использование средств инвестора составляет 10% годовых.Слайд 14БЕСКОНЕЧНЫЙ ПОТОК УВЕЛИЧИВАЮЩИХСЯ ПЛАТЕЖЕЙ
Предположим, что в предыдущей задаче требуется обеспечить
ежегодное увеличение получаемой суммы на 5%. Как определить размер инвестиций
в строительный проект, обеспечивающий такой денежный поток ?Где q – процент увеличение получаемой суммы.
Слайд 15Пример №3:
Требуется определить величину вклада на банковский счет, который обеспечивал
бы ежегодное получение 1000 руб. с увеличением на 5% в
виде процентных платежей в течение бесконечного периода времени. Величина премии за использование банком средств инвестора составляет 10% годовыхСлайд 16Стандартные функции сложного процента для расчета денежных потоков
Настоящая стоимость
единицы (present value reversion of 1) — данная функция соответствует
текущей (на момент оценки) стоимости одной денежной единицы, получаемой через n периодов при i процентах.То есть, если инвестор планирует получить через n периодов некоторую сумму (FV), следовательно, сегодня ему надо отдать сумму, равную PV.
ПРИМЕР:
Какую сумму следует сегодня положить на счет под 10% на 10 лет, чтобы в будущем получить 1000 долл.
Слайд 18Понятие «АННУИТЕТ»
Аннуитетом (аnnuity) или финансовой рентой называют поток одинаковых платежей
А, поступающих через равные промежутки времени. Аннуитет может быть срочным
(имеет ограничение по времени поступления платежей) и бесконечным.Различают два типа срочных аннуитетов: «постнумерандо» и «пренумерандо». В первом случае каждый платеж осуществляется в конце каждого периода, во втором - в начале
Слайд 19Настоящая стоимость аннуитета (пс)- функция, определяющая настоящую стоимость серии будущих
равных единичных платежей в течение n периодов при норме процента,
равной i.Коэффициент настоящей стоимости аннуитета рассчитывается по формуле:
ПРИМЕР:
Если в течение 10 лет строительная фирма каждый год выплачивала 1 долл. при норме 10% то какая сумма была взята в кредит ?
Слайд 20РЕШЕНИЕ
Если в условии было бы сказано, что фирма выплачивала в
течение 10 лет в начале года 1 долл., то решение
выглядело бы так:Слайд 21Будущая стоимость единицы (amount of I at compound interest)(БС) —
это функция, определяющая величину будущей стоимости денежной единицы через n
периодов при сложном проценте, равном i.Коэффициент будущей стоимости единицы рассчитывается по формуле:
ПРИМЕР:
Если сегодня положить в банк 1 долл. под 10%, то сколько можно получить через 10 лет ?
Слайд 23Будущая стоимость аннуитета (БС) — показывает, какова будущая стоимость единичного
аннуитета при заданном числе периодов n и норме процента i.
Коэффициент
будущей стоимости аннуитета рассчитывается по формуле:ПРИМЕР:
Если каждый год откладывать 1 долл. на счет под 10%, то какая сумма будет через 10 лет.
Слайд 25Фактор фонда возмещения (плт) — величина платежа для аннуитета, будущая
стоимость которого через n периодов при заданной норме процента i
равна 1.Коэффициент будущей стоимости аннуитета рассчитывается по формуле:
ПРИМЕР:
Собственник здания знает, что на ремонт кровли уйдет 1 000 у.е., нормативный срок службы данного конструктивного элемента 15 лет. Требуется определить, какую сумму следует ежегодно откладывать собственнику в банк, чтобы через 15 лет накопить сумму на ремонт, если ставка банка равна 18%?
Слайд 27Расчет самоамортизирующегося кредита с постоянной нормой процента
Производится по формуле взноса
на амортизацию единицы (ПЛТ), которая показывает, какой платеж должен быть
в течении n периодов, чтобы их настоящая стоимость при норме процента i была равна 1ПРИМЕР:
Требуется определить величину ежегодной выплаты для самоамортизирующего кредита, суммой 3155 у.е., взятого на 4 года, под 10 % годовых.
Слайд 30ДОПОЛНИТЕЛЬНЫЕ ФУНКЦИИ
1. Количество периодов. Для определения количества периодов (n), можно
воспользоваться функцией КПЕР (ставка; плата; пс; бс; тип).
ПРИМЕР №1:
Если каждый
год вносить по 1000 у.е., то через какой период (сколько лет) на счету будет 16000 у.е., если ставка 10%. ПРИМЕР №2:
Если сегодня положить 10000 рублей, то через сколько лет сумма увеличится вдвое, при ставке 10%.
Слайд 31РЕШЕНИЕ №1
КПЕР (ставка; плата; пс; бс; тип)= (10%;-1000;;16000;0)=10 .
РЕШЕНИЕ №2
КПЕР
(ставка; плата; пс; бс; тип)= (10%;;-10000;20000;0)=7,3
Слайд 32Норма. Для определения i - нормы (ставки, внутренней нормы отдачи
) при равных выплатах, можно воспользоваться функцией СТАВКА (кпер; плт;
пс, бс; тип).ПРИМЕР №1:
Под какой процент нужно вложить 10000 у.е, чтобы через 7 лет получить 20000
у.е.
Для определения i - нормы (ставки, внутренняя норма отдачи) при неравных выплатах можно воспользоваться функцией ВCД (значения), где значения - это массив или ссылка на ячейки, содержащие числовые величины, для которых вычисляется норма. Значения должны включать, по крайней мере, одно положительное значение и одно отрицательное значение, для того, чтобы можно было вычислить ставку.
ПРИМЕР №2:
Чистый операционный доход первого года работы строительной организации будет равен 100 тыс. у.е., и будет увеличиваться на 2 тыс. у.е. в год в течение 4 лет эксплуатации. После этого объект будет продан за 1000 у.е. Вычислить внутреннюю норму отдачи для проекта, если требуются начальные инвестиции в сумме 800 тыс. у.е..
Слайд 33РЕШЕНИЕ №1
СТАВКА (кпер; плт; пс, бс; тип)= (7;;-10000;20000;0)=10,41%.
РЕШЕНИЕ №2
ВCД
(значения) = (-800,100,102,104,1106)=17,64% .
Создаем массив денежных потоков:
в момент времени 0
- -800;в момент времени 1 – 100;
в момент времени 2 – 102;
в момент времени 3 – 104;
в момент времени 4 – 106+1000.
2. Вводим весь массив в функцию ВСД
3. Вычисляем значение функции ВСД
Слайд 34Текущая стоимость неравномерного потока. Функция ЧПС (ставка; значение 1; значение2;...),
где ставка — ставка процента, значение1- доход (выплата, платеж) первого
года; значение 2 - доход (выплата, платеж) второго года и т.д. данную функцию часто используют для расчета NPV. Чистая текущая стоимость (NPV) - дисконтированная стоимость всех будущих денежных потоков, минус начальные инвестиции.ПРИМЕР №1:
Чистый операционный доход первого года будет равен 100 тыс. у.е., и будет увеличиваться на 2 тыс. у.е. в год, после 4 лет эксплуатации объект будет продан за 1000 тыс. у.е. Найти чистую текущую стоимость проекта, если требуются начальные инвестиции в сумме 800 тыс. у.е., а норма дисконтирования 10%.
где Со - начальные инвестиции,
/ - ежегодный доход (например, NOI),
Vn- доход от продажи объекта (реверсии).
Слайд 35РЕШЕНИЕ
Создаем массив положительных денежных потоков:
в момент времени 1 – 100;
в
момент времени 2 – 102;
в момент времени 3 – 104;
в
момент времени 4 – 106+1000.2. Вводим ставку и весь массив в функцию ЧПС
3. Вычисляем значение функции ЧПС = (0,1;100;102;104;1106) =1009
4. Вычисляем текущую стоимость проекта 1009-800=209