Тема 4:

Содержание

1. Тема 4:
2. Оптимальный приёмник  устройство обработки, обеспечивающее наилучшее
3. Задачи, решаемые в теории оптимального приёма сигналовОбнаружение
4. Априорная и апостериорная вероятностиa priori  «из
5. Формула полной вероятностиСовместная плотность вероятности отсчётов и параметра 
6. 5Формула Байеса. Функция правдоподобияФункция правдоподобия
7. Функция правдоподобия параметра сигнала, принимаемого на фоне
8. Функция правдоподобия при ограниченной частоте fвАКФ шумаОтсчёты
9. Функция правдоподобия при ограниченной частоте fвНормальное распределение вероятностей отсчётов:
10. Функция правдоподобия при
11. Апостериорная плотность вероятности параметраОценка параметра по критерию максимума апостериорной вероятности:
12. Скачать презентанцию

Оптимальный приёмник  устройство обработки, обеспечивающее наилучшее выделение полезной информации из сигнала, принимаемого в смеси с аддитивной шумовой помехой Шумовая помеха  нормальный белый шум Синтез оптимального приёмника 

Слайды и текст этой презентации

Слайд 1Тема 4:
Основы оптимальной обработки сигналов.
Оптимальная оценка параметра сигнала.

Слайд 2Оптимальный приёмник  устройство обработки, обеспечивающее наилучшее выделение полезной информации

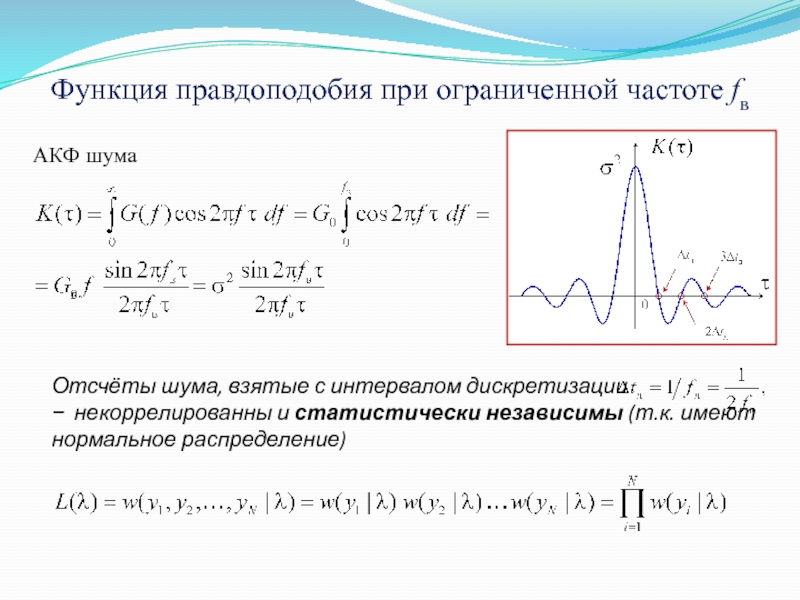
из сигнала, принимаемого в смеси с аддитивной шумовой помехой

Шумовая помеха  нормальный белый шум

Синтез оптимального приёмника  нахождение структуры и параметров устройства обработки, обеспечивающее наилучшее выделение полезной информации из определённого типа сигнала

Критерий оптимальности приёмника  правило, которое определяет, какой способ выделения полезной информации считается наилучшим

Примеры:
- критерий минимума СКО
- критерий максимума апостериорной вероятности

Основные понятия

Оптимальный приёмник  устройство обработки, обеспечивающее наилучшее выделение полезной информации из сигнала, принимаемого в смеси с аддитивной

Слайд 3Задачи, решаемые в теории оптимального приёма сигналов
Обнаружение сигнала на фоне

помех
Различение двух или нескольких сигналов на фоне помех
Оценка одного или

нескольких параметров сигнала, принимаемого в смеси с помехами
Фильтрация (выделение) сигнала из смеси с помехами

(Задачи 1 и 2 – частный случай задачи 3)

изучаются в курсе

Задачи, решаемые в теории оптимального приёма сигналовОбнаружение сигнала на фоне помехРазличение двух или нескольких сигналов на фоне

Слайд 4Априорная и апостериорная вероятности
a priori  «из предыдущего» (до «опыта»)
a

posteriori  «из последующего» (после «опыта»)
До начала обработки известно (априорная

информация):
вид сигнала
распределение вероятностей шума
априорное распределение вероятностей параметра 

Принимаемая смесь сигнала и шума:

Обрабатываются N отсчётов принятого колебания:

10.1. Оптимальная оценка параметра сигнала

или реализация

Априорная и апостериорная вероятностиa priori  «из предыдущего» (до «опыта»)a posteriori  «из последующего» (после «опыта»)До начала

Слайд 5Формула полной вероятности
Совместная плотность вероятности отсчётов и параметра

Слайд 65
Формула Байеса. Функция правдоподобия
Функция правдоподобия

 условная плотность вероятности отсчётов принятой смеси сигнала и шума, рассматриваемая как функция параметра 

Слайд 7Функция правдоподобия параметра сигнала, принимаемого на фоне нормального белого шума
1-й

шаг - находим функцию правдоподобия при следующих условиях:

2-й шаг -

переходим к пределу:

Функция правдоподобия параметра сигнала, принимаемого на фоне нормального белого шума1-й шаг - находим функцию правдоподобия при следующих

Слайд 8Функция правдоподобия при ограниченной частоте fв
АКФ шума

Отсчёты шума, взятые с

интервалом дискретизации  некоррелированны и

статистически независимы (т.к. имеют нормальное распределение)

Функция правдоподобия при ограниченной частоте fвАКФ шумаОтсчёты шума, взятые с интервалом дискретизации

Слайд 9Функция правдоподобия при ограниченной частоте fв
Нормальное распределение вероятностей отсчётов:

Слайд 10Функция правдоподобия при

Слайд 11Апостериорная плотность вероятности параметра
Оценка параметра по критерию максимума апостериорной вероятности:

Скачать презентацию

Разделы презентаций

Тема 4:

Содержание

Слайды и текст этой презентации

Слайд 1Тема 4:
Основы оптимальной обработки сигналов.
Оптимальная оценка параметра сигнала.

Слайд 2Оптимальный приёмник  устройство обработки, обеспечивающее наилучшее выделение полезной информации

из сигнала, принимаемого в смеси с аддитивной шумовой помехой

Слайд 3Задачи, решаемые в теории оптимального приёма сигналов
Обнаружение сигнала на фоне

помех
Различение двух или нескольких сигналов на фоне помех
Оценка одного или

Слайд 4Априорная и апостериорная вероятности
a priori  «из предыдущего» (до «опыта»)
a

posteriori  «из последующего» (после «опыта»)
До начала обработки известно (априорная

Слайд 5Формула полной вероятности
Совместная плотность вероятности отсчётов и параметра

Слайд 65
Формула Байеса. Функция правдоподобия
Функция правдоподобия

Слайд 7Функция правдоподобия параметра сигнала, принимаемого на фоне нормального белого шума
1-й

шаг - находим функцию правдоподобия при следующих условиях:

2-й шаг -

Слайд 8Функция правдоподобия при ограниченной частоте fв
АКФ шума

Отсчёты шума, взятые с

интервалом дискретизации  некоррелированны и

Слайд 9Функция правдоподобия при ограниченной частоте fв
Нормальное распределение вероятностей отсчётов:

Слайд 10Функция правдоподобия при

Слайд 11Апостериорная плотность вероятности параметра
Оценка параметра по критерию максимума апостериорной вероятности:

Обратная связь

Что такое TheSlide.ru?

Разделы презентаций

Тема 4:

Содержание

Слайды и текст этой презентации

Слайд 1Тема 4:Основы оптимальной обработки сигналов. Оптимальная оценка параметра сигнала.

Слайд 2Оптимальный приёмник  устройство обработки, обеспечивающее наилучшее выделение полезной информации

из сигнала, принимаемого в смеси с аддитивной шумовой помехой

Слайд 3Задачи, решаемые в теории оптимального приёма сигналовОбнаружение сигнала на фоне

помехРазличение двух или нескольких сигналов на фоне помехОценка одного или

Слайд 4Априорная и апостериорная вероятностиa priori  «из предыдущего» (до «опыта»)a

posteriori  «из последующего» (после «опыта»)До начала обработки известно (априорная

Слайд 5Формула полной вероятностиСовместная плотность вероятности отсчётов и параметра

Слайд 65Формула Байеса. Функция правдоподобияФункция правдоподобия

Слайд 7Функция правдоподобия параметра сигнала, принимаемого на фоне нормального белого шума1-й

шаг - находим функцию правдоподобия при следующих условиях:2-й шаг -

Слайд 8Функция правдоподобия при ограниченной частоте fвАКФ шумаОтсчёты шума, взятые с

интервалом дискретизации  некоррелированны и

Слайд 9Функция правдоподобия при ограниченной частоте fвНормальное распределение вероятностей отсчётов:

Слайд 10Функция правдоподобия при

Слайд 11Апостериорная плотность вероятности параметраОценка параметра по критерию максимума апостериорной вероятности:

Похожие презентации

Обратная связь

Что такое TheSlide.ru?

Слайд 1Тема 4:
Основы оптимальной обработки сигналов.
Оптимальная оценка параметра сигнала.

Слайд 3Задачи, решаемые в теории оптимального приёма сигналов
Обнаружение сигнала на фоне

помех
Различение двух или нескольких сигналов на фоне помех
Оценка одного или

Слайд 4Априорная и апостериорная вероятности
a priori  «из предыдущего» (до «опыта»)
a

posteriori  «из последующего» (после «опыта»)
До начала обработки известно (априорная

Слайд 5Формула полной вероятности
Совместная плотность вероятности отсчётов и параметра

Слайд 65
Формула Байеса. Функция правдоподобия
Функция правдоподобия

Слайд 7Функция правдоподобия параметра сигнала, принимаемого на фоне нормального белого шума
1-й

шаг - находим функцию правдоподобия при следующих условиях:

2-й шаг -

Слайд 8Функция правдоподобия при ограниченной частоте fв
АКФ шума

Отсчёты шума, взятые с

Слайд 9Функция правдоподобия при ограниченной частоте fв
Нормальное распределение вероятностей отсчётов:

Слайд 11Апостериорная плотность вероятности параметра
Оценка параметра по критерию максимума апостериорной вероятности: