Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тема: Объем шара и его частей. Решение задач
Содержание
- 1. Тема: Объем шара и его частей. Решение задач
- 2. 14.04.2020 Дистанционная работа.Объем шара и его частей. Решение задач.
- 3. Объём шараи его частейПОВТОРИМ ФОРМУЛЫ
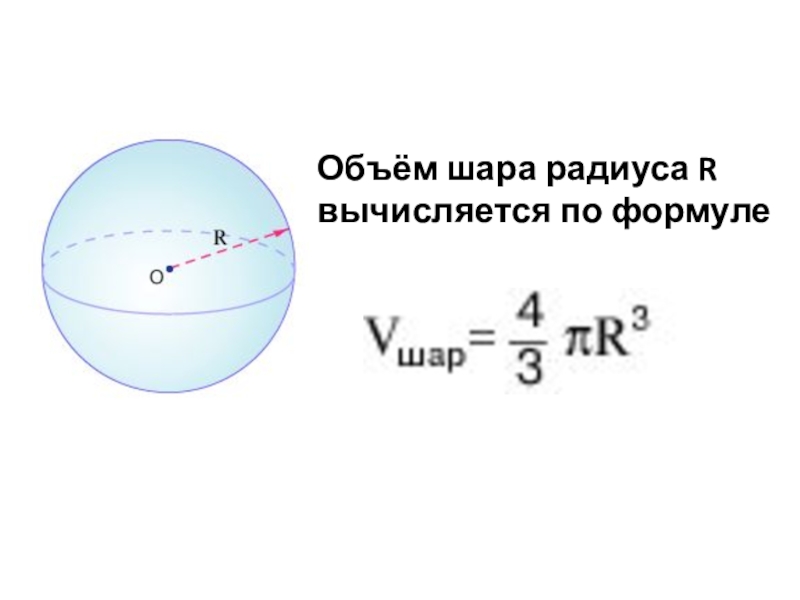
- 4. Объём шара радиуса R вычисляется по формуле
- 5. Шаровой сегмент и
- 6. Шаровой сегмент и
- 7. Шаровой сектор
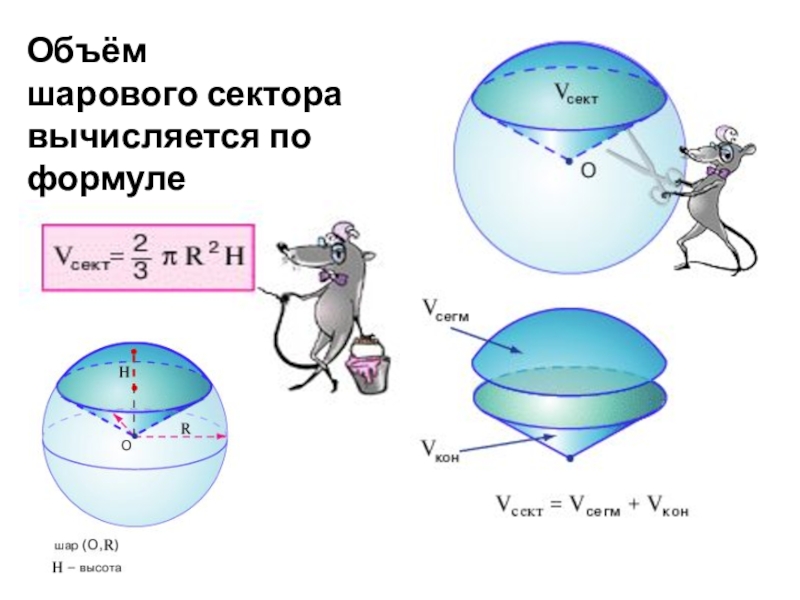
- 8. Объём шарового сектора вычисляется по формуле
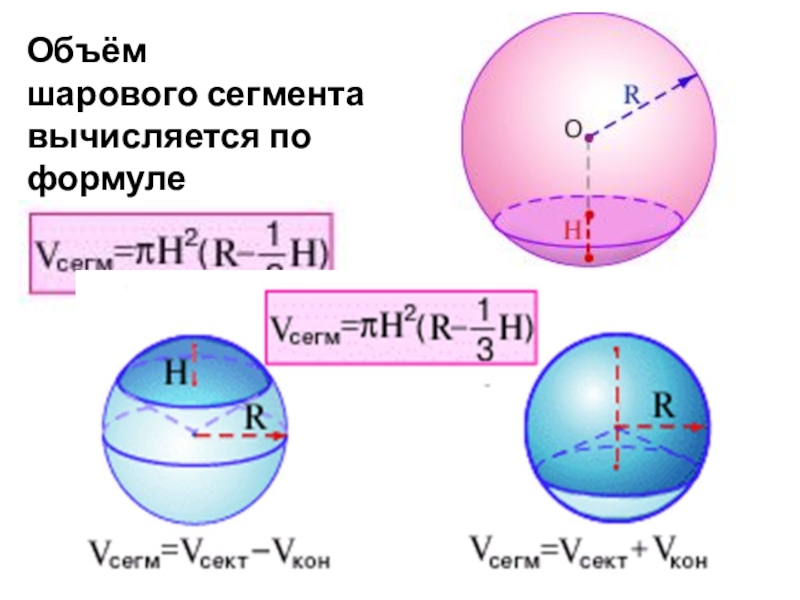
- 9. Объём шарового сегментавычисляется по формуле
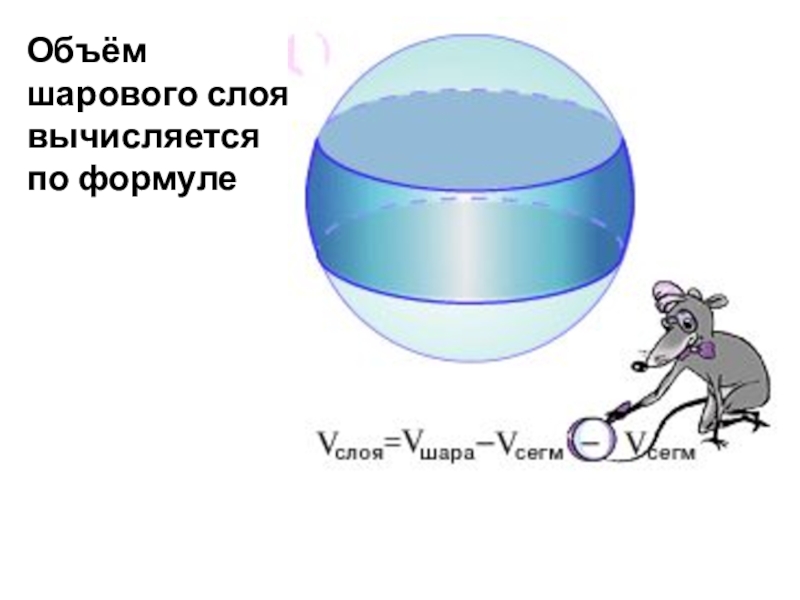
- 10. Объём шарового слоявычисляется по формуле
- 11. ПРОБЛЕМНАЯ ЗАДАЧА: При уличной торговле арбузами весы
- 12. Решение:
- 13. Задача (Архимеда): На надгробном камне могилы Архимеда
- 14. Эти отношения и соотношения следует выделить и запомнить!!!
- 15. Задача Площадь поверхности полушара равна 48
- 16. ЗадачаСтаканчик для мороженого конической формы
- 17. Решение.1) Найдём объём стаканчика, имеющего коническую форму.
- 18. Задача Сколько кубометров земли потребуется
- 19. Пусть АС = h, AB = r,
- 20. Тест «Проверь себя»1) Выбери формулу для вычисления
- 21. Ответы:бгббва
- 22. Решить самостоятельноЗадача №1Около шара описан цилиндр, площадь
- 23. Задача №3 Радиусы трех шаров равны 6,
- 24. Слайд 24
- 25. Скачать презентанцию
14.04.2020 Дистанционная работа.Объем шара и его частей. Решение задач.
Слайды и текст этой презентации
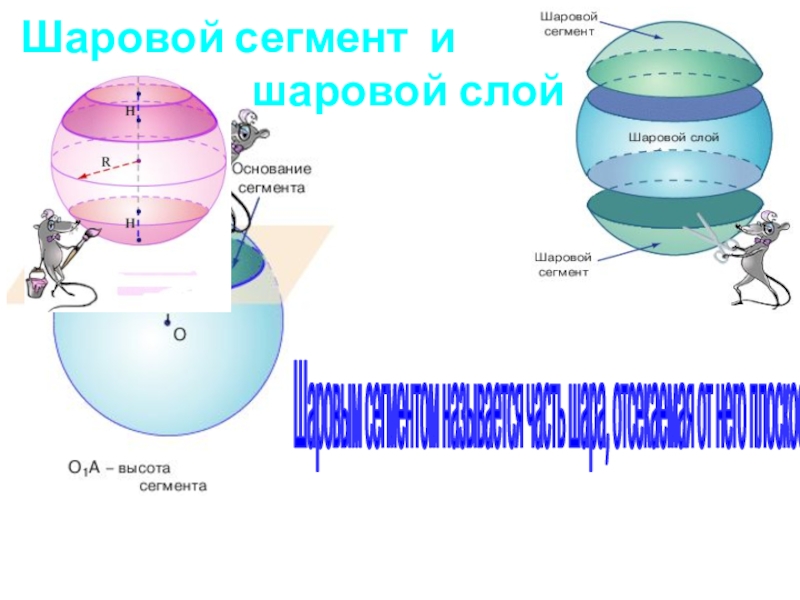
Слайд 5Шаровой сегмент и
шаровой слой
Шаровым сегментом называется часть шара,
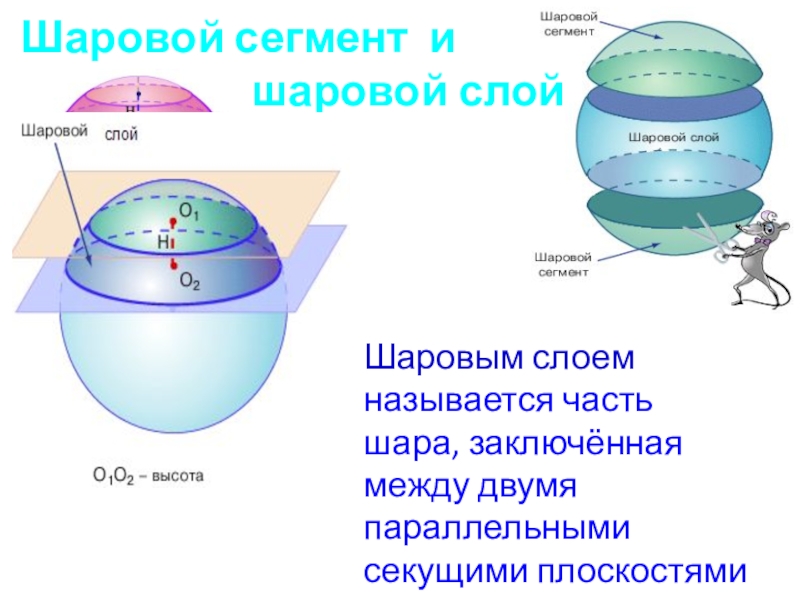
отсекаемая от него плоскостью Слайд 6Шаровой сегмент и
шаровой слой
Шаровым слоем называется часть шара,
заключённая между двумя параллельными секущими плоскостями Слайд 7Шаровой сектор
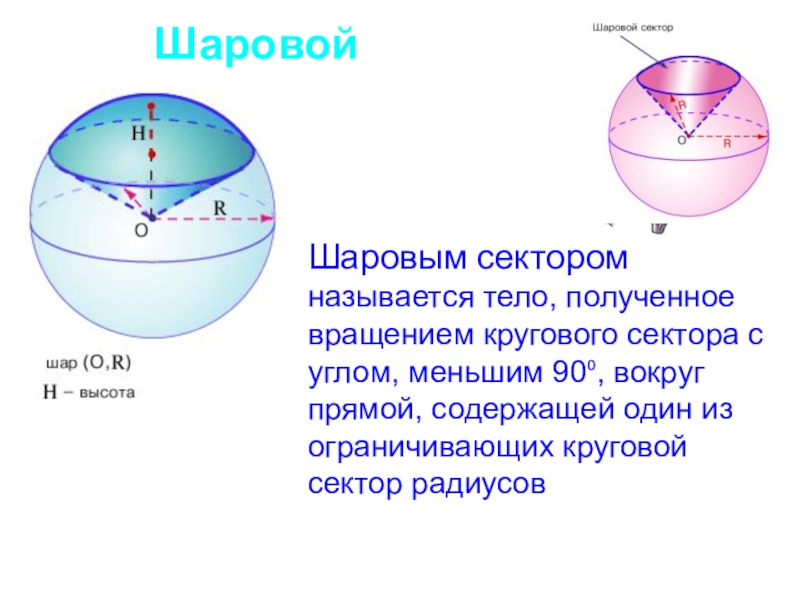
Шаровым сектором называется тело, полученное вращением
кругового сектора с углом, меньшим 90⁰, вокруг прямой, содержащей один из ограничивающих круговой сектор радиусов Слайд 11ПРОБЛЕМНАЯ ЗАДАЧА: При уличной торговле арбузами весы отсутствовали. Однако выход
был найден: арбуз диаметром 3 дм приравнивали по стоимости к
трём арбузам диаметром 1 дм.Что вы возьмете? Правы ли были продавцы?
Слайд 13Задача (Архимеда):
На надгробном камне могилы Архимеда в Сиракузах изображен
цилиндр с вписанным в него шаром. Это символ открытия формул
объема шара и площади сферы, а также важного вывода, что «объем шара, вписанного в цилиндр в …раз меньше объема цилиндра и что также относятся площади поверхностей этих тел». Найдите отношение объема цилиндра к объему шара и отношение площади поверхности цилиндра к площади поверхности шара.Слайд 16Задача
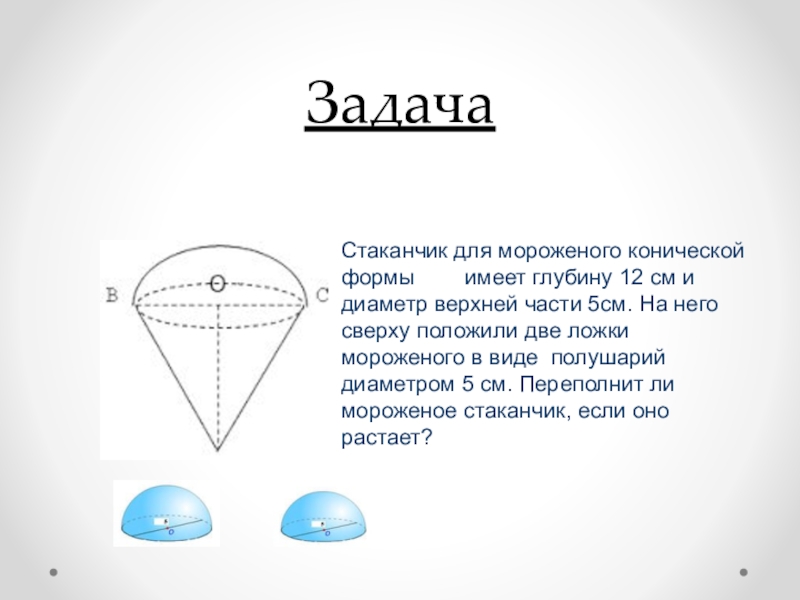
Стаканчик для мороженого конической формы имеет глубину
12 см и диаметр верхней части 5см. На него сверху
положили две ложки мороженого в виде полушарий диаметром 5 см. Переполнит ли мороженое стаканчик, если оно растает?Слайд 17Решение.
1) Найдём объём стаканчика, имеющего коническую форму. Так как D=CB
= 5см, то R = OB=2, 5см.
Пользуясь формулой ,
получаем
2) Сумма объёмов двух полушарий равных диаметров равна объёму шара с тем же диаметром. Найдём объём шара с диаметром
D = 5 см.
3) Сравним полученные объёмы: Vk. > Vш.
Ответ: растаявшее мороженое стаканчик не переполнит.
Слайд 18Задача
Сколько кубометров земли потребуется для устройства клумбы,
имеющей форму шарового сегмента с радиусом основания 5 м
и высотой 60 см?Слайд 19Пусть АС = h, AB = r, r — радиус
клумбы; примем радиус шара равным Рассмотрим центральное сечение шара.
CD
= 2R, ∟CBD = 90°, т.к. он опирается на диаметр CD.
Из треугольника CDB. СВ = 2R cosα; из ∆ACB:
Слайд 20Тест «Проверь себя»
1) Выбери формулу для вычисления объёма шара:
а)
б) в) г)2) Найдите радиус шара, если его объём равен 972см³:
а)13см б) 7 см в) 5 см г)9 см
3) Объём одного шара равен сумме объёмов двух других шаров. Как связаны между собой диаметры D1, D2, D3 этих шаров?
4) Радиус конуса равен 4 см, а высота равна 2 см. Найдите радиус шара, имеющего тот же объёма:
а) 2П б)2 в)8 г)√2
5) У арбуза диаметр 20 см, а толщина корки 2 см. Какая часть арбуза приходится на корку?
а) 0,25 б) 0,37 в) 0,488 г) 0,2
6) В шар вписан цилиндр с квадратным осевым сечением, а в него вписан новый шар. Отношение объёмов исходного и нового шаров равно:
а) б) в) г) 4
Слайд 22Решить самостоятельно
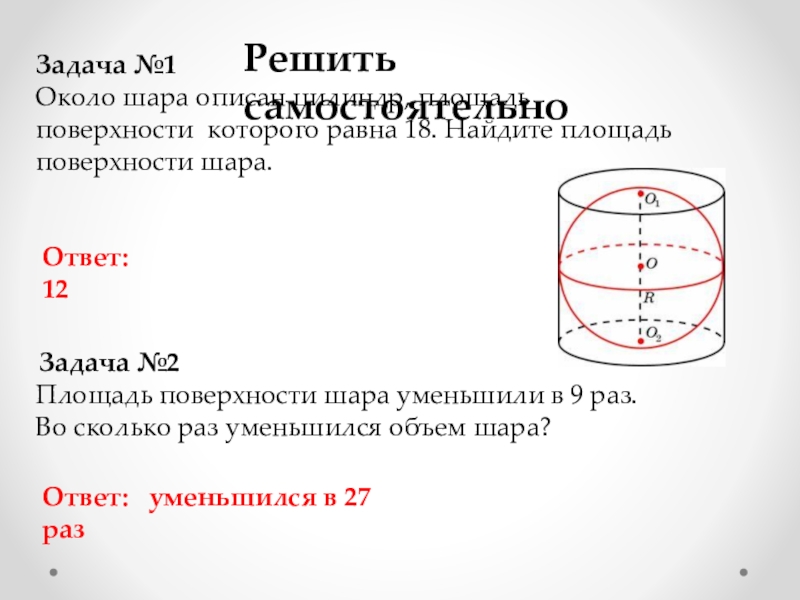
Задача №1
Около шара описан цилиндр, площадь поверхности которого равна
18. Найдите площадь поверхности шара.
Ответ: 12
Задача №2
Площадь поверхности шара уменьшили
в 9 раз. Во сколько раз уменьшился объем шара?Ответ: уменьшился в 27 раз
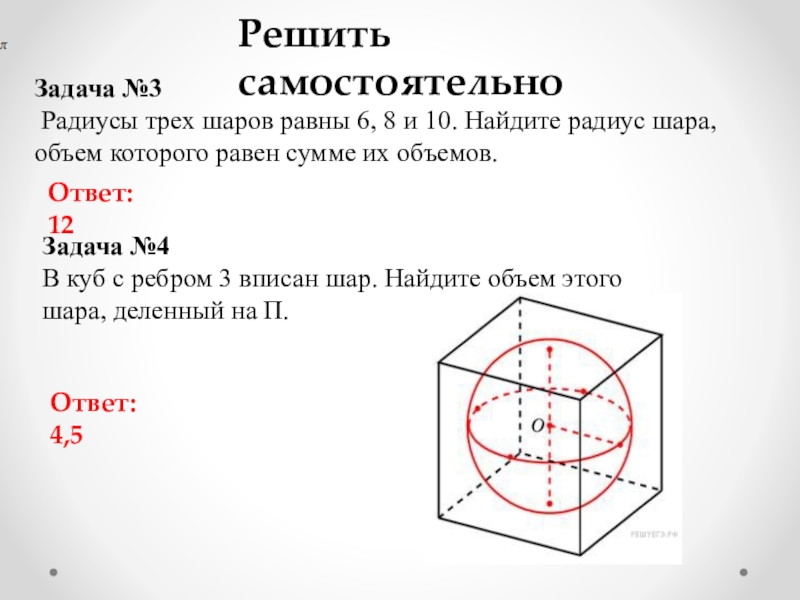
Слайд 23Задача №3
Радиусы трех шаров равны 6, 8 и 10.
Найдите радиус шара, объем которого равен сумме их объемов.
Ответ:
12Задача №4
В куб с ребром 3 вписан шар. Найдите объем этого шара, деленный на П.
Ответ: 4,5
Решить самостоятельно