Слайд 1ТЕМА "ПРИМЕНЕНИЕ ПОЛЯРНЫХ КООРДИНАТ ДЛЯ ОПРЕДЕЛЕНИЯ МЕСТОПОЛОЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ"
Выполнила студентка
группы а11 кузуб анна
Преподаватель Тавгер ефим хаймович
ПРОЕКТНАЯ РАБОТА
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ
УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «БАЛТИЙСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ ИМЕНИ ИММАНУИЛА КАНТА»
(БФУ ИМ. И. КАНТА)
ИНСТИТУТ ПРИРОДОПОЛЬЗОВАНИЯ, ТЕРРИТОРИАЛЬНОГО РАЗВИТИЯ И ГРАДОСТРОИТЕЛЬСТВА
СПЕЦИАЛЬНОСТЬ 07.03.02 АРХИТЕКТУРА
Слайд 2СОДЕРЖАНИЕ
ЦЕЛИ, ЗАДАЧИ, АКТУАЛЬНОСТЬ
ВВЕДЕНИЕ
ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ
УРАВНЕНИЕ КРИВЫХ В ПОЛЯРНЫХ КООРДИНАТАХ
КОМПЛЕКСНЫЕ ЧИСЛА
МАТЕМАТИЧЕСКИЙ АНАЛИЗ
ТРЁХМЕРНОЕ
РАСШИРЕНИЕ
ПРИМЕНЕНИЕ
ЗАКЛЮЧЕНИЕ
ИСПОЛЬЗОВАННЫЕ ИСТОЧНИКИ
Слайд 3ЦЕЛИ: изучение полярной системы координат и приобретение навыка нахождения положения точки
с помощью полярных координат.
ЗАДАЧИ: изучить полярную систему координат, охарактеризовать процесс нахождения материальной точки
с помощью полярных координат.
АКТУАЛЬНОСТЬ: данная тема актуальна, так как не изучается в школьной программе, несмотря на то, что не все графики удобно строить в декартовой системе.
Слайд 4ВВЕДЕНИЕ
Полярная система координат - двухмерная система координат, в которой каждая
точка на плоскости определяется двумя числами - полярным углом и
полярным радиусом. Полярная система координат особенно полезна в случаях, когда отношения между точками проще изобразить в виде радиусов и углов; в более распространённой декартовой, или прямоугольной, системе координат, такие отношения можно установить только путём применения тригонометрических уравнений.
Слайд 51. ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ
Каждая точка в полярной системе координат может быть
определена двумя полярными координатами, что обычно называются r (радиальная координата,
встречается вариант обозначения р) и φ (угловая координата, полярный угол, фазовый угол, азимут, позиционный угол, иногда пишут О или t). Координата r соответствует расстоянию от точки до центра, или полюса системы координат, а координата φ равна углу, отсчитываемого в направлении против часовой стрелки от луча через 0° (иногда называемому полярной осью системы координат).
Слайд 62. УРАВНЕНИЕ КРИВЫХ В ПОЛЯРНЫХ КООРДИНАТАХ
Благодаря радиальной природе полярной системы
координат, некоторые кривые могут быть достаточно просто описаны полярным уравнением,
тогда как уравнение в прямоугольной системе координат было бы намного сложнее. Среди самых известных кривых: полярная роза, архимедова спираль, Лемниската, улитка Паскаля и кардиоида.
Слайд 73. КОМПЛЕКСНЫЕ ЧИСЛА
Каждое комплексное число может быть представлено точкой на
комплексной плоскости, и, соответственно, эта точка может определяться в декартовых
координатах (прямоугольная или декартова форма), либо в полярных координатах (полярная форма). Комплексное число z может быть записано в прямоугольной форме так:
z=x+iy, где i - мнимая единица,
или в полярной:
z=rcdot (cos φ +isin φ)
и отсюда:
z=reiφ, где e - число Эйлера
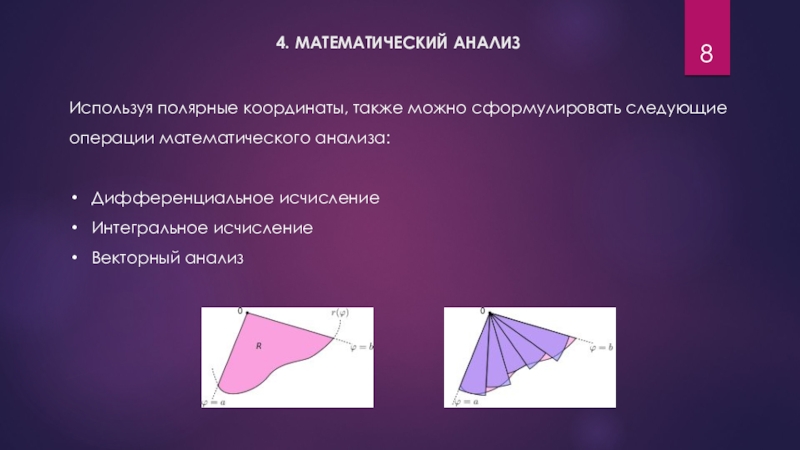
Слайд 84. МАТЕМАТИЧЕСКИЙ АНАЛИЗ
Используя полярные координаты, также можно сформулировать следующие операции математического
анализа:
Дифференциальное исчисление
Интегральное исчисление
Векторный анализ
Слайд 95. ТРЁХМЕРНОЕ РАСШИРЕНИЕ
Полярная система координат распространяется в третье измерение двумя
системами: цилиндрической и сферической, обе содержат двумерную полярную систему координат
как подмножество. По сути, цилиндрическая система расширяет полярную добавлением ещё одной координаты расстояния, а сферическая - ещё одной угловой координаты.
Слайд 106. ПРИМЕНЕНИЕ
В позиционировании и навигации: полярную систему координат часто применяют
в навигации, поскольку пункт назначения можно задать как расстояние и
направление движения от отправной точки;
В физике: существенное удобство полярные координаты предоставляют при работе с системами, имеющими точечные (или приближенно точечные) источники энергии;
В прикладных целях: в разных прикладных областях, полярные координаты применяются как способами, близкими к применяемым в соответствующих областям фундаментальной физики, так и самостоятельным образом;
В диаграммах направленности: полярные диаграммы могут использоваться для представления практически любых зависимостей.
Слайд 11ЗАКЛЮЧЕНИЕ
Полярная система координат двумерная и поэтому может применяться только в
тех случаях, когда местонахождение точки определяется на плоскости, или для
случая однородности свойств системы в третьем измерении, например, при рассмотрении течения в круглой трубе. Лучшим контекстом применения полярных координат являются случаи, тесно связанные с направлением и расстоянием от некоторого центра. Кроме того, многие физических системы - такие, которые содержат тела, движущиеся вокруг центра, либо явления, распространяющиеся из некоторого центра - гораздо проще моделировать в полярных координатах.
Слайд 12ИСПОЛЬЗОВАННЫЕ ИСТОЧНИКИ
1. G., Brown Richard. Advanced Mathematics: Precalculus with Discrete Mathematics
and Data Analysis. Evanston, Illinois : McDougal Littell, 1997.
2. Lee, Theodore
и David Cohen, David Sklar. Precalculus: With Unit-Circle Trigonometry, Fourth Edition. б.м. : Thomson Brooks/Cole, 2005.
3. Stewart, Ian и Tall, David. Complex Analysis (the Hitchhiker's Guide to the Plane). б.м. : Cambridge University Press, 1983.
4. Serway, Raymond A. и Jewett, Jr., John W. Principles of Physics. б.м. : Brooks/Cole—Thomson Learning, 2005.
5. Torrence, Bruce Follett и Torrence, Eve. The Student's Introduction to Mathematica. б.м. : Cambridge University Press, 1999.
6. Smith, Julius O. Mathematics of the Discrete Fourier Transform (DFT). б.м. : W3K Publishing, 2003.
7. Гельфанд И. М., Глаголева Е. Г., Кириллов А. А. Метод координат. 1973.