Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тема: Уравнение касательной в общем виде
Содержание
- 1. Тема: Уравнение касательной в общем виде
- 2. Эпиграф занятия «При изучении наук примеры не менее поучительны, нежели правила» И.Ньютон
- 3. Значение производной функции y= f(x)
- 4. Причем, если : . Геометрический смысл производной
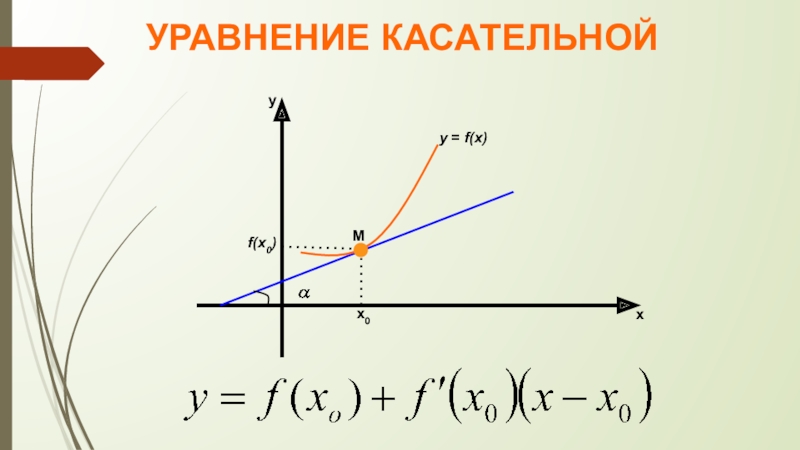
- 5. УРАВНЕНИЕ КАСАТЕЛЬНОЙМхх0уy = f(x)f(x0)
- 6. 1.Обозначим абсциссу точки касания буквой x0.2.Вычислим
- 7. Напишите уравнение касательной к графику функции у=f(x)
- 8. Спасибо за работу!
- 9. Скачать презентанцию
Эпиграф занятия «При изучении наук примеры не менее поучительны, нежели правила» И.Ньютон
Слайды и текст этой презентации
Слайд 3Значение производной функции y= f(x) в точке касания
х0 равно угловому коэффициенту касательной к графику функции
y=f(x) в точке х0.Геометрический смысл производной
Слайд 61.Обозначим абсциссу точки касания буквой x0.
2.Вычислим
.
3.Найдем и
.4.Подставим найденные числа x0, и в формулу
Алгоритм нахождения уравнения касательной к графику функции y=f(x).
Слайд 7Напишите уравнение касательной к графику функции у=f(x) в точке с
абсциссой x0
f(x) = х²+ х+1,
x0=2
1.f(2)=22+2+1=7
2. f/
= 2х=13. f/(2) = 2*2+1=5
4. y=7+5(x-2)=7+5x-10=5x-3
k= f/(2)=5>0, угол острый, функция возрастает.
Ответ: y=5x-3