Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тема урока
Содержание
- 1. Тема урока
- 2. Цели урокаПознакомить учащихся с содержанием курса стереометрии;Показать
- 3. Школьный курс геометрии состоит из двух частей:ПЛАНИМЕТРИИПланиметрия-это
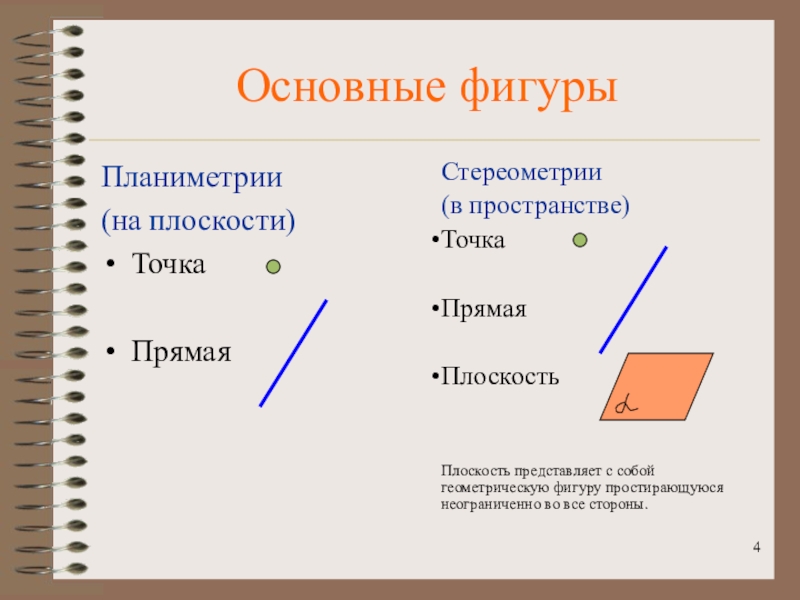
- 4. Основные фигуры Планиметрии(на плоскости)Точка ПрямаяСтереометрии (в пространстве)ТочкаПрямаяПлоскостьПлоскость
- 5. Наряду с точками, прямыми, плоскостями в стереометрии
- 6. Модели геометрических телпараллелепипедпирамидаконусцилиндршаркуб
- 7. Точки обозначаются прописными латинскими буквами А, В,
- 8. Стереометрия широко используется в строительном деле
- 9. Архитектуре
- 10. Машиностроении
- 11. ГеодезииВо многих других областях науки и техники.Геодезия - наука, занимающаяся изучением вида и размера Земли.
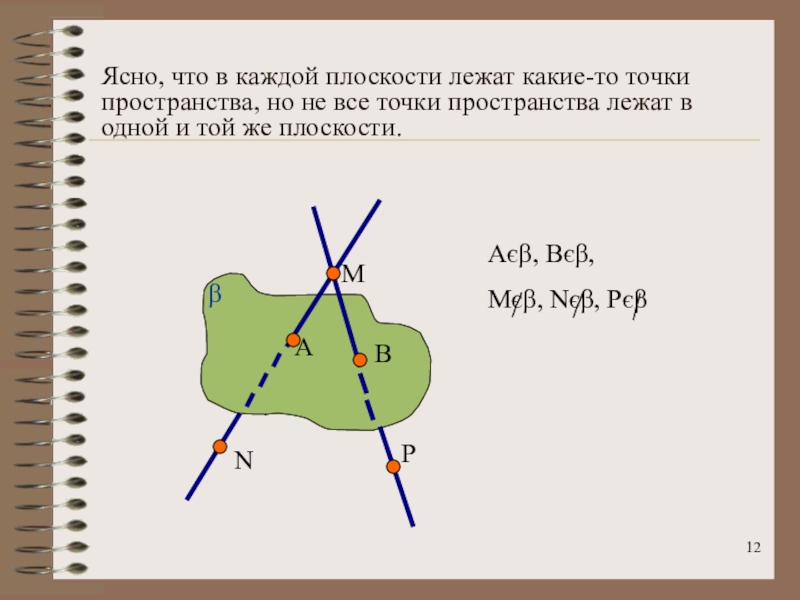
- 12. Ясно, что в каждой плоскости
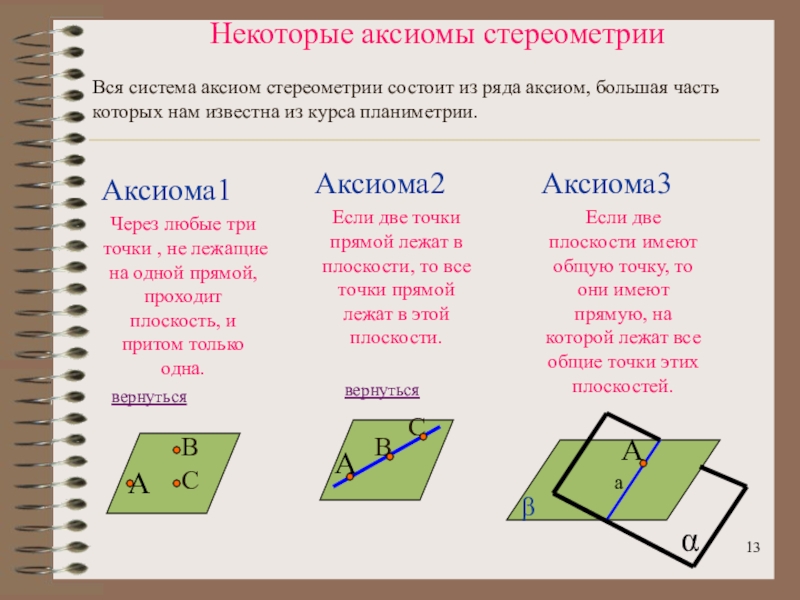
- 13. Некоторые аксиомы стереометрииАксиома1Через любые три точки ,
- 14. Некоторые следствия из аксиомТеорема1.Через прямую и не
- 15. Теорема2. Через две пересекающиеся прямые проходит плоскость,
- 16. Скачать презентанцию
Цели урокаПознакомить учащихся с содержанием курса стереометрии;Показать связь курса стереометрии с практической деятельностью людей;Изучить три аксиомы о взаимном расположении точек, прямых и плоскостей в пространстве.
Слайды и текст этой презентации
Слайд 2Цели урока
Познакомить учащихся с содержанием курса стереометрии;
Показать связь курса стереометрии
с практической деятельностью людей;
прямых и плоскостей в пространстве.
Слайд 3Школьный курс геометрии состоит из двух частей:
ПЛАНИМЕТРИИ
Планиметрия-это раздел геометрии, в
котором изучаются свойства геометрических фигур на плоскости.
СТЕРЕОМЕТРИИ
Стереометрия-это раздел геометрии, в
котором изучаются свойства фигур в пространстве.
Слово «стереометрия» происходит от греческих слов «стереос» - объемный, пространственный
и «метрео» - измерять.
Слайд 4Основные фигуры
Планиметрии
(на плоскости)
Точка
Прямая
Стереометрии
(в пространстве)
Точка
Прямая
Плоскость
Плоскость представляет с собой
геометрическую фигуру простирающуюся неограниченно во все стороны.
Слайд 5Наряду с точками, прямыми, плоскостями в стереометрии рассматриваются геометрические тела,
изучаются их свойства, вычисляются площади их поверхностей, а также вычисляются объёмы
тел.шар
куб
цилиндр
Слайд 7Точки обозначаются прописными латинскими буквами А, В, С, D, Е,
К,…
Прямые обозначаются строчными латинскими буквами a, b, c, d, e,
k,… Плоскости обозначаются греческими буквами α, β, γ, λ, π, ω,…
А
В
С
Е
a
b
d
α
β
γ
Слайд 11Геодезии
Во многих других областях науки и техники.
Геодезия - наука, занимающаяся
изучением вида и размера Земли.
Слайд 12 Ясно, что в каждой плоскости лежат какие-то точки пространства, но
не все точки пространства лежат в одной и той же
плоскости.М
А
N
P
B
Aє, Bє,
Mє, Nє, Pє
Слайд 13Некоторые аксиомы стереометрии
Аксиома1
Через любые три точки , не лежащие на
одной прямой, проходит плоскость, и притом только одна.
Аксиома2
Если две точки
прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.Аксиома3
Если две плоскости имеют общую точку, то они имеют прямую, на которой лежат все общие точки этих плоскостей.
А
В
С
А
В
С
а
α
А
Вся система аксиом стереометрии состоит из ряда аксиом, большая часть которых нам известна из курса планиметрии.
вернуться
вернуться
Слайд 14Некоторые следствия из аксиом
Теорема1.Через прямую и не лежащую на ней
точку проходит плоскость, и притом только одна.
P
а
Q
M
α
Дано: прямая а,
Мєа, Доказать: Мєα, аєα,
Доказательство: 1)Возьмем две точки Рєа и Qєа.
2)Через три точки, М, Р, Q по аксиоме А1 можно провести плоскость, притом только одну.
3)Если две точки Рєα и Qєα, то по аксиоме А2 прямая аєα , значит Мєα, аєα.
4)Существование единственной плоскости следует из А1.
Теорема доказана.
Слайд 15Теорема2. Через две пересекающиеся прямые проходит плоскость, и притом только
одна.
M
N
b
a
α
Дано: прямые а∩b=М,
Доказать: аєα, bєα,
Доказательство: 1) Возьмем точку
Nєb.2) По теореме1, через прямую и не лежащую в ней точку, проведем плоскость α, получим аєα и Nєα
3)Имеем Мєb( по условию) и Nєb , следовательно bєα по аксиоме А2.
4)Значит аєα и bєα..
5)Существование единственной плоскости следует из теоремы1.
Теорема доказана.
