Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА СТАТИКА
Содержание
- 1. ТЕОРЕТИЧЕСКАЯ МЕХАНИКА СТАТИКА
- 2. 2.1 Момент силы относительно центра (точки)
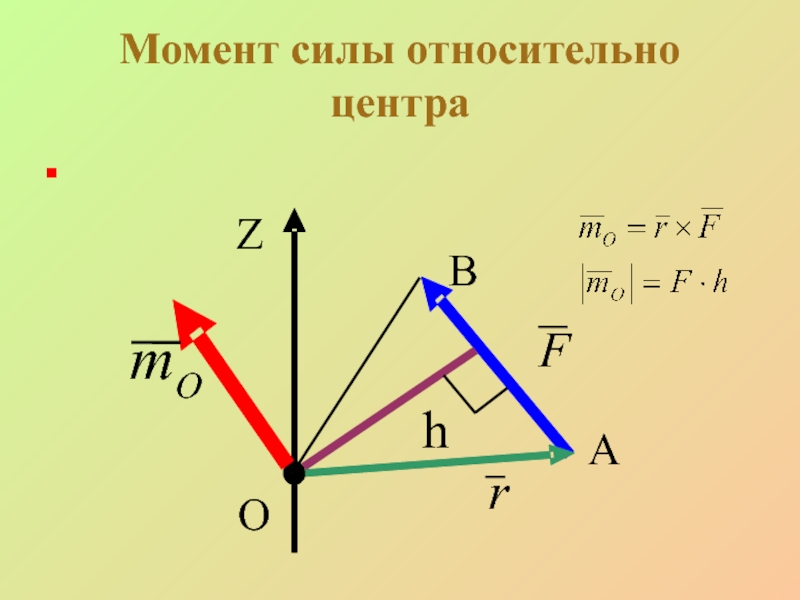
- 3. Момент силы относительно центра A F O h Z B Om r
- 4. Слайд 4
- 5. Свойства момента силы:
- 6. Слайд 6
- 7. Слайд 7
- 8. Пьер ВариньонПьер Вариньон (фр. Pierre Varignon, Кан, 1654 —
- 9. Теорема Вариньона
- 10. 2.2 Теория пар сил, свойства пар сил
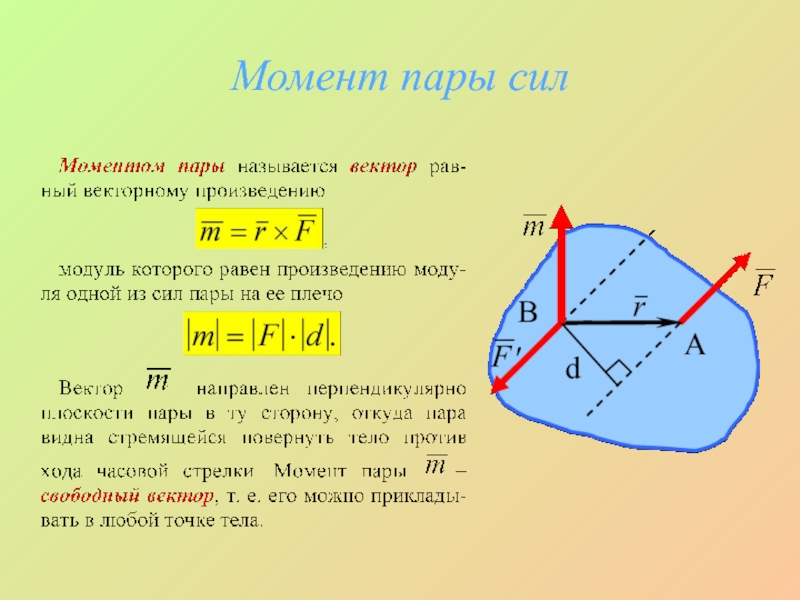
- 11. Момент пары сил
- 12. Свойства пар сил
- 13. Слайд 13
- 14. Слайд 14
- 15. Слайд 15
- 16. 2.3 Приведение системы сил к заданному центруТеорема Пуансо
- 17. Пуансо Луи Пуансо (Poinsot) Луи (3.1.1777, Париж,
- 18. Теорема1 - О параллельном переносе силы
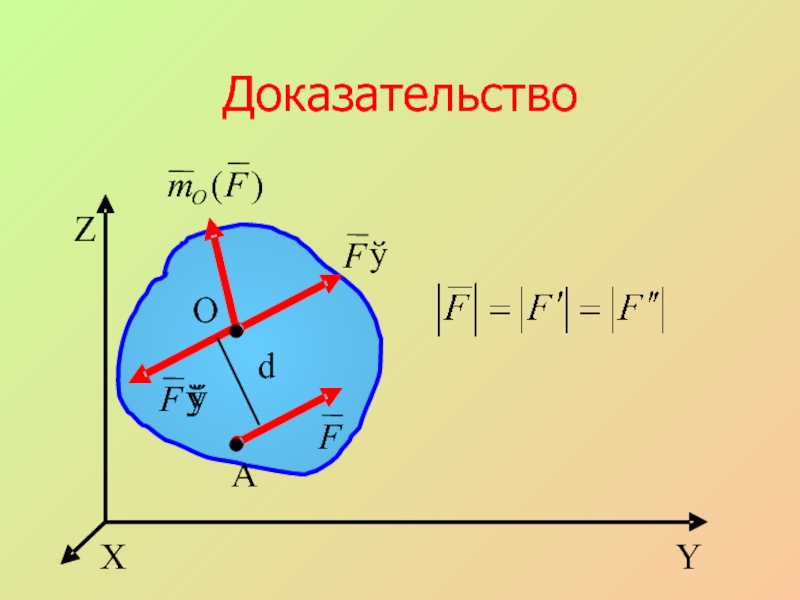
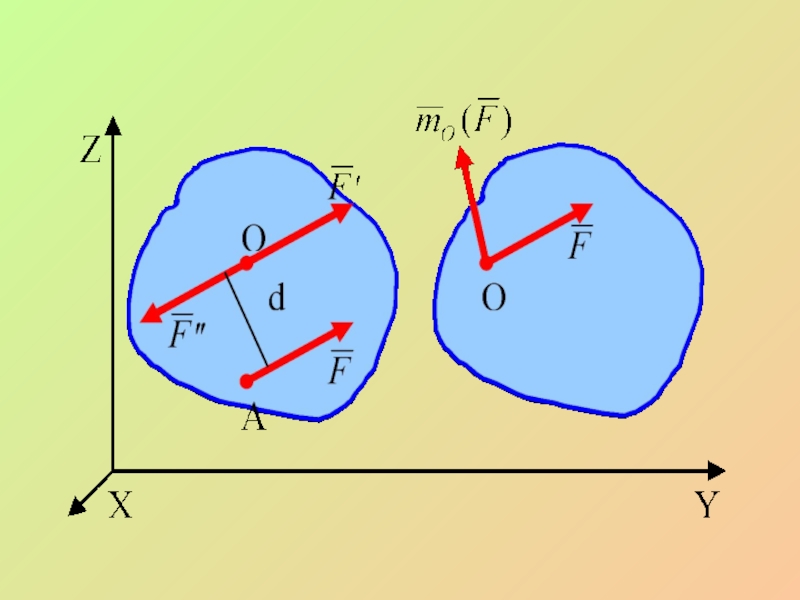
- 19. Доказательство X Y Z A O d
- 20. Слайд 20
- 21. Теорема 2 – О приведении системы сил
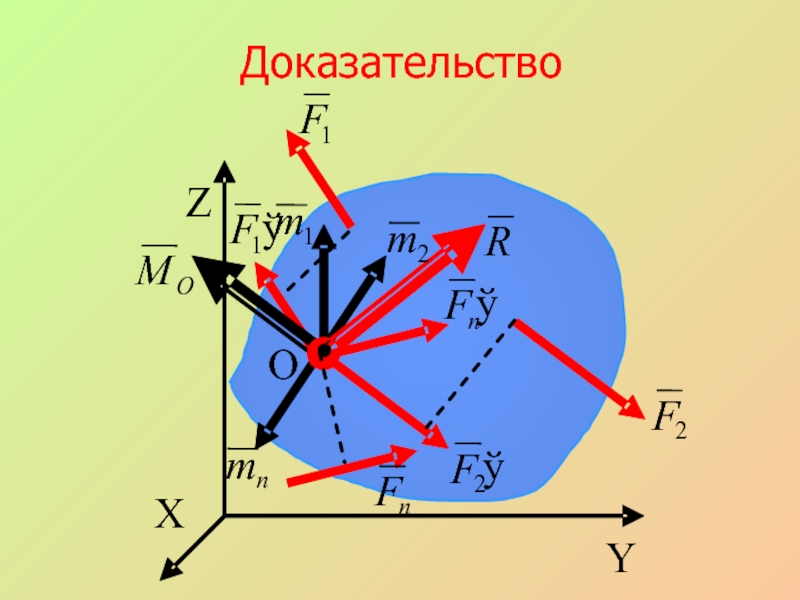
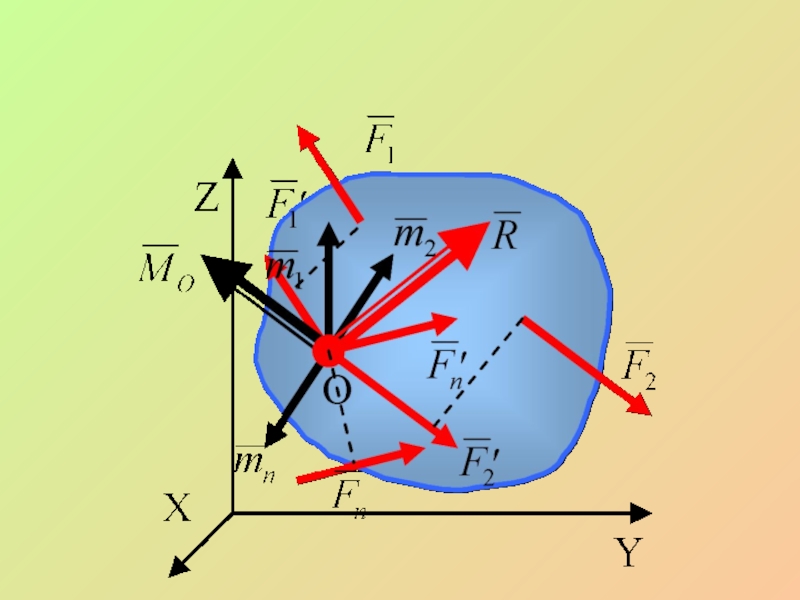
- 22. Доказательство X Z Y O
- 23. Слайд 23
- 24. Используя теорему 1 перенесем все силы в
- 25. Для плоской системы сил главный вектор
- 26. Частные случаи приведения системы сил:
- 27. система сил приводится к равнодействующей , приложенной
- 28. система сил уравновешена. Теорема: Для равновесия
- 29. РАВНОВЕСИЕ ПРОИЗВОЛЬНОЙ ПЛОСКОЙ СИСТЕМЫ СИЛ Необходимые и
- 30. Основная форма условий равновесиядля сил, лежащих в
- 31. Вторая форма условий равновесия:Для равновесия произвольной плоской
- 32. Слайд 32
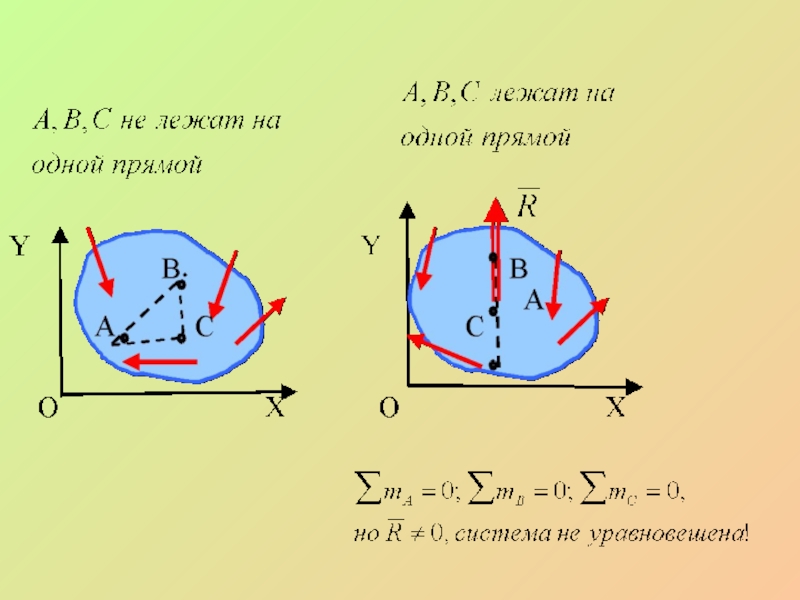
- 33. Третья форма условий равновесияДля равновесия произвольной плоской
- 34. Слайд 34
- 35. Для проверки решения задачи на равновесие
- 36. Скачать презентанцию
2.1 Момент силы относительно центра (точки)
Слайды и текст этой презентации
Слайд 8Пьер Вариньон
Пьер Вариньон (фр. Pierre Varignon, Кан, 1654 — 23 декабря, 1722,
Париж) — французский математик, член Парижской Академии наук, профессор математики коллежа
Мазарини (1688), профессор Коллеж де Франс.[1] Обучался в иезуитском коллеже и университете в Кане, где стал магистром в 1682 году.Вариньон был другом Ньютона, Лейбница и Бернулли. Основной вклад Вариньон совершил в статику и механику; кроме того, труды Вариньона посвящены анализу бесконечно малых, геометрии, гидромеханике. За исключением Лопиталя, Вариньон был самым первым пропагандистом дифференциального исчисления во Франции. В 1687 году в своей работе «Проект новой механики…» Вариньон дал точную формулировку закона параллелограмма сил, развил понятие момента сил и вывел теорему, получившую имя Вариньона. В работе «Новая механика или статика, проект которой был дан в 1687» (1725) Вариньон дал систематическое изложение учения о сложении и разложении сил, о моментах сил и о правилах оперирования ими.[1]
Слайд 17Пуансо Луи
Пуансо (Poinsot) Луи (3.1.1777, Париж, — 5.12.1859, там же),
французский математик и механик, член Парижской АН с 1813. Окончил
Политехническую школу в Париже (1797), с 1809 профессор там же. В период Июльской монархии — в Министерстве народного образования. Пэр Франции (1846), сенатор (1852). Первые работы П. посвящены теории правильных звездчатых многогранников. В 1803 опубликовал "Элементы статики", в которых применил разработанные им геометрические методы исследования к учению о равновесии твёрдых тел и их систем. В 1834 построил теорию вращения твёрдого тела вокруг неподвижной точки. Впервые ввёл понятие эллипсоида вращения.Слайд 18Теорема1 - О параллельном переносе силы
(лемма Пуансо):
силу ,
не изменяя ее действия на абсолютно твердое тело, можно переносить
из данной точки А в любую другую точку О тела, прибавляя при этом пару с моментом равным моменту переносимой силы относительно точки О, в которую переносится сила .Слайд 21Теорема 2 – О приведении системы сил к заданному центру
(теорема Пуансо):
Любая система сил , действующая на абсолютно твердое тело,
при приведении к произвольному центру О заменяется главным вектором системы сил, приложенным в центре О и парой сил с моментом , равным главному моменту системы сил относительно центра О.Слайд 24Используя теорему 1 перенесем все силы в центр О прибавляя
пары с моментами равными моментам сил относительно центра О. Сложив
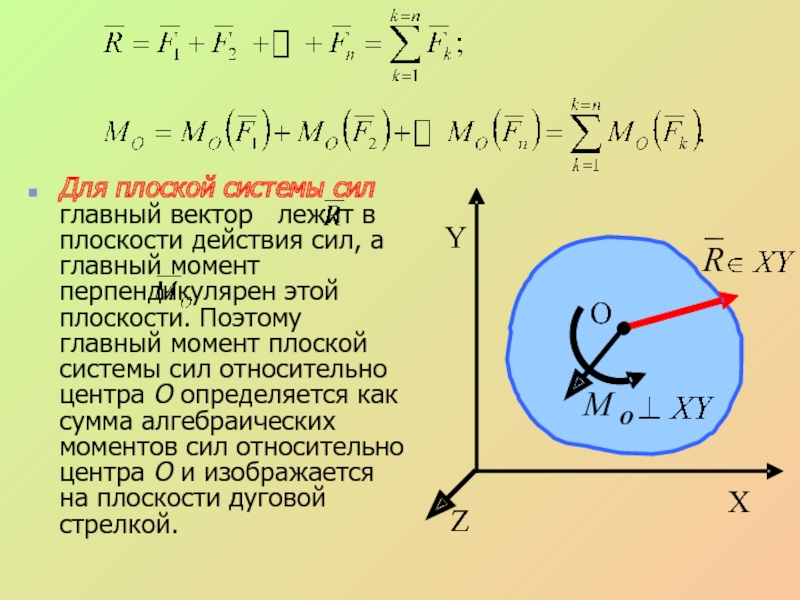
все силы и моменты получим в центре О два вектора и равные:Слайд 25Для плоской системы сил главный вектор лежит в плоскости
действия сил, а главный момент перпендикулярен этой плоскости. Поэтому
главный момент плоской системы сил относительно центра О определяется как сумма алгебраических моментов сил относительно центра О и изображается на плоскости дуговой стрелкой.X
Y
O
Z
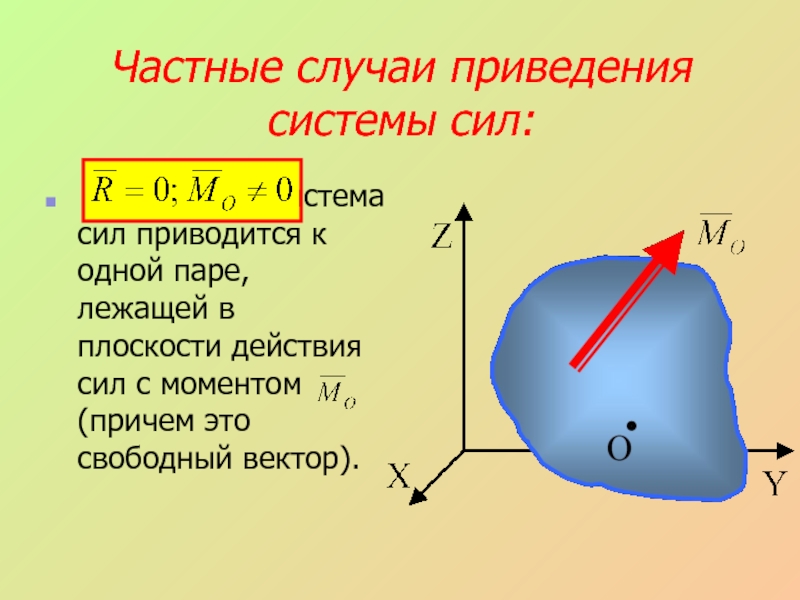
Слайд 26Частные случаи приведения системы сил:
система сил приводится к одной паре,
лежащей в плоскости действия сил с моментом (причем это свободный вектор).Слайд 27
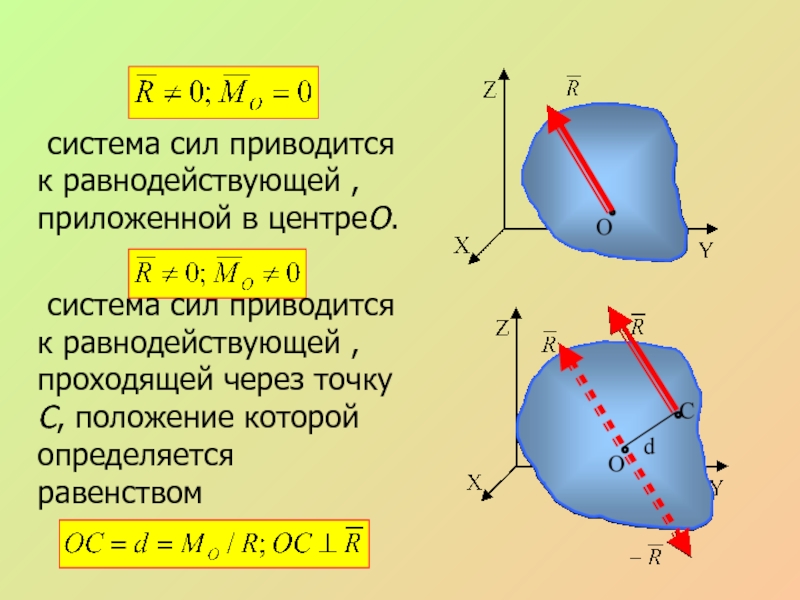
система сил приводится к равнодействующей , приложенной в центреО.
система сил
приводится к равнодействующей , проходящей через точку С, положение которой
определяется равенствомСлайд 28
система сил уравновешена.
Теорема: Для равновесия любой системы сил
необходимо и достаточно, чтобы главный вектор и главный момент этой
системы относительно любого центра (точки) были равны нулю.Слайд 29РАВНОВЕСИЕ ПРОИЗВОЛЬНОЙ ПЛОСКОЙ СИСТЕМЫ СИЛ
Необходимые и достаточные условия равновесия
твердого тела, находящегося под действием произвольной плоской системы сил в
векторной форме имеют видИз этих векторных уравнений следуют три формы аналитических условий равновесия.
Слайд 30Основная форма условий равновесия
для сил, лежащих в плоскости ОХУ:
Для равновесия
произвольной плоской системы сил необходимо и достаточно, чтобы сумма проекций
сил на каждую из координатных осей и сумма моментов сил относительно любой точки, лежащей в плоскости действия сил, были равны нулю.Слайд 31Вторая форма условий равновесия:
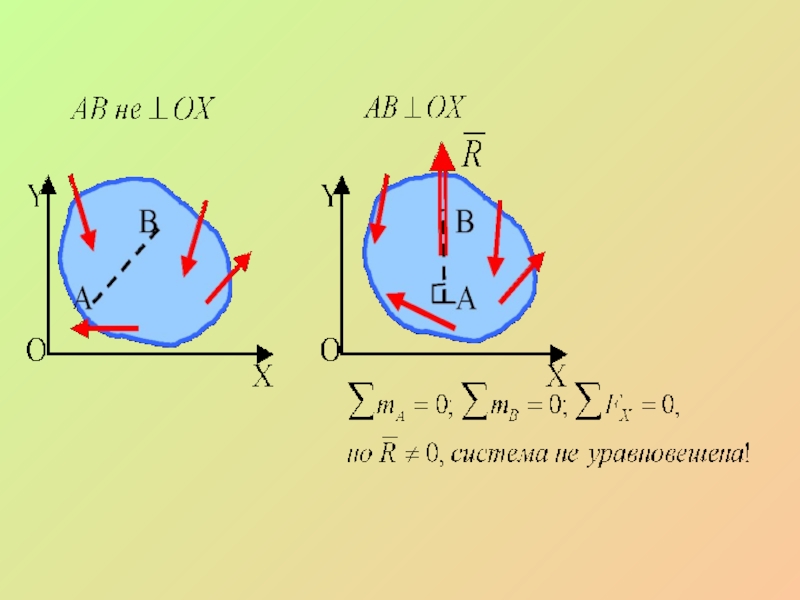
Для равновесия произвольной плоской системы сил необходимо
и достаточно, чтобы суммы моментов всех сил относительно двух точек
А и В и сумма их проекций на ось ОX,не перпендикулярную прямой АВ, были равны нулю.