Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ТЕОРИЯ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ Курс читает: к.т.н., доцент Журавлев Илья
Содержание
- 1. ТЕОРИЯ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ Курс читает: к.т.н., доцент Журавлев Илья
- 2. План курса1.Комплексные числа (напоминание).2.Общие сведения о системах
- 3. Комплексные числа
- 4. Теория автоматического управления (ТАУ):1.Принцип управления(как нужно управлять).2.Математические модели.3.Устойчивость работы.4.Качество управления.
- 5. Общие сведения о системах управления
- 6. Система управления (из чего состоит?)
- 7. Система управления (регулятор)
- 8. Система управления (из чего состоит?)
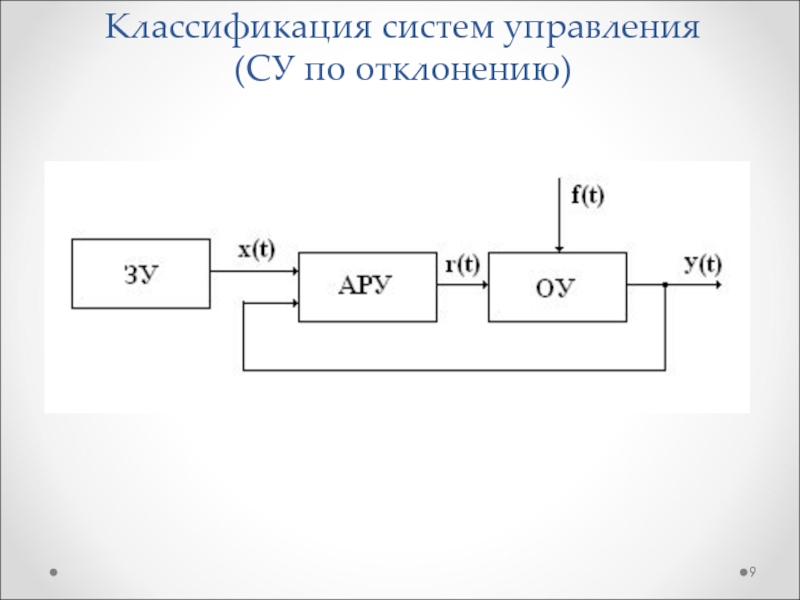
- 9. Классификация систем управления (СУ по отклонению)
- 10. Классификация систем управления (СУ по возмущению)
- 11. Классификация систем управления (СУ с комбинированным управлением)
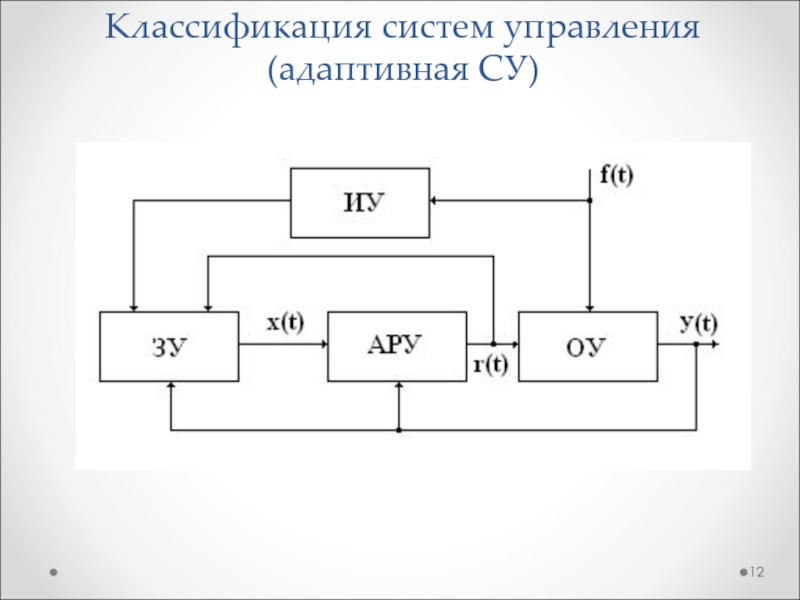
- 12. Классификация систем управления (адаптивная СУ)
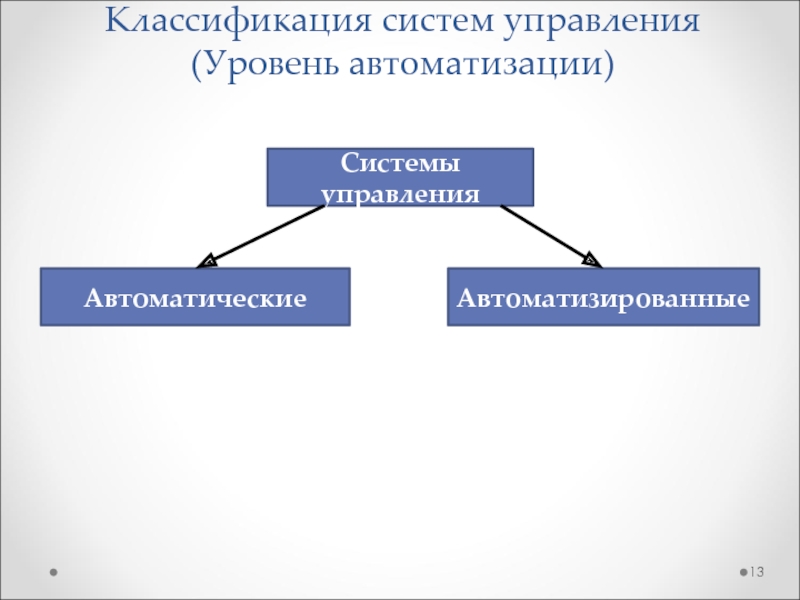
- 13. Классификация систем управления (Уровень автоматизации)Системы управленияАвтоматическиеАвтоматизированные
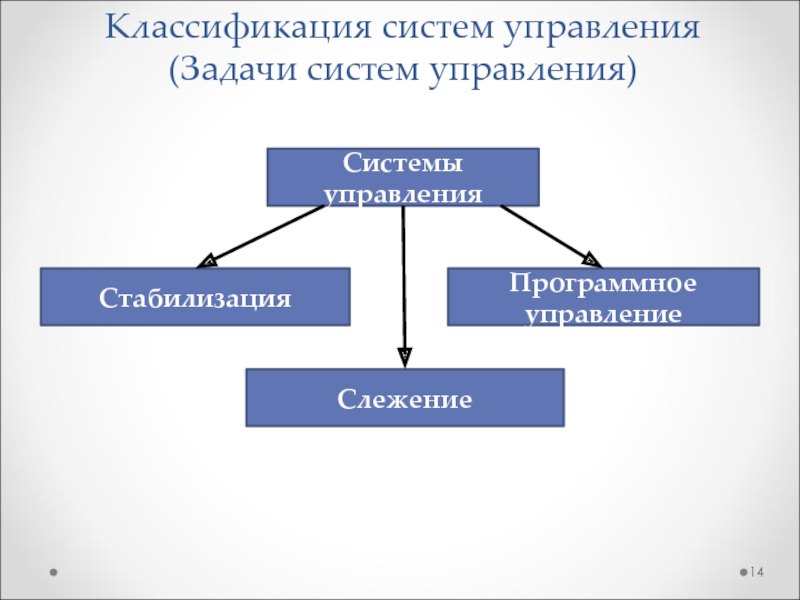
- 14. Классификация систем управления (Задачи систем управления)Системы управленияСтабилизацияПрограммное управлениеСлежение
- 15. Классификация систем управления (По количеству входов и выходов)Системы управленияОдномерныеМногомерные
- 16. Классификация систем управления (Характер сигналов системы)Системы управленияНепрерывныеДискретныеНепрерывно-дискретные
- 17. Классификация систем управления (Характер сигналов системы)СистемыАвтоматического управления (САУ)Автоматического регулирования (САР)
- 18. Математические модели
- 19. Линейность и нелинейность Цель любого управления – изменить
- 20. Описание элементов Способы описания динамических свойств:Дифференциальные уравнения;Передаточные функции W(p);Временные функции;Частотные характеристики.РежимыСтатический Динамический
- 21. Дифференциальные уравненияЗдесь:y(t) – временная функция выходного сигнала;x(t)
- 22. Передаточная функция Передаточная функция W(p) есть отношение выходного
- 23. Переходная характеристикаЕдиничный ступеньчатый сигнал
- 24. Импульсная характеристика (весовая функция)Единичный импульсный сигнал
- 25. Разложение дроби на сумму элементарных дробейИмеем
- 26. Таблица оригиналов и изображений (обратное/прямое преобразование Лапласа)
- 27. Частотные характеристики Частотные характеристики САУ характеризуют реакцию систем на синусоидальное входное воздействие в установившемся режиме.Частотные характеристикиАЧХАФЧХФЧХЛАЧХЛФЧХ
- 28. Частотные характеристики Зная передаточную функцию W(p), можно получить
- 29. Логарифмические частотные характеристики- ось ординат- ось абсциссЛАЧХ- ось ординат- ось абсциссЛФЧХ(Дб)(Декада)(Декада) Свойства:1)2) Асимптотические ЛАЧХ
- 30. Типовые динамические звенья
- 31. Усилитель- Передаточная функция- Переходная характеристика- Импульсная характеристика- АЧХ- ФЧХ, ЛФЧХ- ЛАЧХ
- 32. Апериодическое звено- Передаточная функция- Переходная характеристика- Импульсная характеристика- АФЧХ- ЛАЧХ
- 33. Апериодическое звено Переходная характеристикаИмпульсная характеристикаАФЧХЛАЧХЛФЧХ
- 34. Колебательное звено- Передаточная функция- АФЧХ- ЛАЧХ
- 35. Колебательное звено Переходная характеристикаИмпульсная характеристикаАФЧХЛАЧХЛФЧХ
- 36. Интегрирующее звено- Передаточная функция- Переходная характеристика- Импульсная характеристика- АФЧХ- ЛАЧХ
- 37. Интегрирующее звено Переходная характеристикаИмпульсная характеристикаАФЧХЛАЧХЛФЧХ
- 38. Идеально дифференцирующее звено- Передаточная функция- Переходная характеристика-
- 39. Идеально дифференцирующее звено Переходная характеристикаАФЧХЛАЧХЛФЧХ
- 40. Форсирующее звено- Передаточная функция- Переходная характеристикаФизически не реализуемое- АФЧХ- ЛАЧХ
- 41. Форсирующее звено Переходная характеристикаАФЧХЛАЧХЛФЧХ
- 42. Построение ЛАЧХРассмотрим звено второго порядка с передаточной
- 43. Структурные схемы
- 44. Структурное преобразование схемРазветвление сигнала: Параллельное и последовательное соединение звеньев:
- 45. Структурное преобразование схемДля контура с отрицательной обратной
- 46. Структурное преобразование схемПрямой перенос суммирующего звена: Обратный перенос сигнала через ПФ:
- 47. Структурное преобразование схемПрямой перенос суммирующего звена: Обратный перенос суммирующего звена:
- 48. Передаточные функции системПередаточная функция по возмущающему воздействию: Передаточная функция по управлениюПередаточная функция по рассогласованию:
- 49. Анализ САУ
- 50. Анализ САУТребования к управлениюТочностьКачествоУстойчивостьРаботоспособность
- 51. Критерии устойчивости (критерий Гурвица)Пример для полинома пятого
- 52. Критерии устойчивости (критерий Найквиста)Система устойчива тогда и
- 53. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2План курса
1.Комплексные числа (напоминание).
2.Общие сведения о системах управления.
3. Математические
модели.
Слайд 4Теория автоматического управления (ТАУ):
1.Принцип управления
(как нужно управлять).
2.Математические модели.
3.Устойчивость работы.
4.Качество управления.
Слайд 13Классификация систем управления
(Уровень автоматизации)
Системы управления
Автоматические
Автоматизированные
Слайд 14Классификация систем управления
(Задачи систем управления)
Системы управления
Стабилизация
Программное управление
Слежение
Слайд 15Классификация систем управления
(По количеству входов и выходов)
Системы управления
Одномерные
Многомерные
Слайд 16Классификация систем управления
(Характер сигналов системы)
Системы управления
Непрерывные
Дискретные
Непрерывно-дискретные
Слайд 17Классификация систем управления
(Характер сигналов системы)
Системы
Автоматического управления (САУ)
Автоматического регулирования (САР)
Слайд 19Линейность и нелинейность
Цель любого управления – изменить состояние объекта нужным
образом.
Модель – это объект, который используется для изучения другого объекта
(оригинала).Оператор
Линейный
Нелинейный
Свойства:
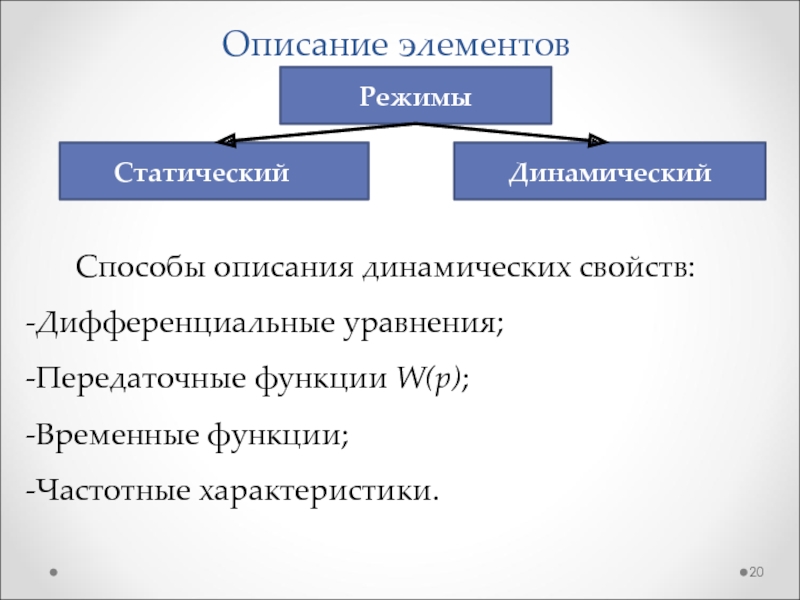
Слайд 20Описание элементов
Способы описания динамических свойств:
Дифференциальные уравнения;
Передаточные функции W(p);
Временные функции;
Частотные характеристики.
Режимы
Статический
Динамический
Слайд 21Дифференциальные уравнения
Здесь:
y(t) – временная функция выходного сигнала;
x(t) – временная функция
входного сигнала;
y(j)(t) – j-я производная функции y(t);
x(j)(t) – j-я производная
функции x(t);am, bm – постоянные коэффициенты уравнения при соответствующих переменных.
Слайд 22Передаточная функция
Передаточная функция W(p) есть отношение выходного сигнала к входному
сигналу, представленное в операторной форме:
Заменим d/dt на оператор Лапласа –
p и получим:Слайд 25Разложение дроби
на сумму элементарных дробей
Имеем рациональную дробь R(x) вида:
где
степени m>n.
Дробь такого вида можно представить, притом единственным образом, в
виде суммы элементарных дробей:где A, B, C — некоторые действительные коэффициенты, обычно вычисляемые с помощью метода неопределённых коэффициентов.
Слайд 27Частотные характеристики
Частотные характеристики САУ характеризуют реакцию систем на синусоидальное входное
воздействие в установившемся режиме.
Частотные характеристики
АЧХ
АФЧХ
ФЧХ
ЛАЧХ
ЛФЧХ
Слайд 28Частотные характеристики
Зная передаточную функцию W(p), можно получить амплитудно-фазовую частотную характеристику,
путем замены оператора Лапласа – p , на мнимое число
– jw.- АФЧХ
- АЧХ
- ФЧХ
где -
Слайд 29Логарифмические частотные характеристики
- ось ординат
- ось абсцисс
ЛАЧХ
- ось ординат
- ось
абсцисс
ЛФЧХ
(Дб)
(Декада)
(Декада)
Свойства:
1)
2) Асимптотические ЛАЧХ
Слайд 31Усилитель
- Передаточная функция
- Переходная характеристика
- Импульсная характеристика
- АЧХ
- ФЧХ, ЛФЧХ
-
ЛАЧХ
Слайд 32Апериодическое звено
- Передаточная функция
- Переходная характеристика
- Импульсная характеристика
- АФЧХ
- ЛАЧХ
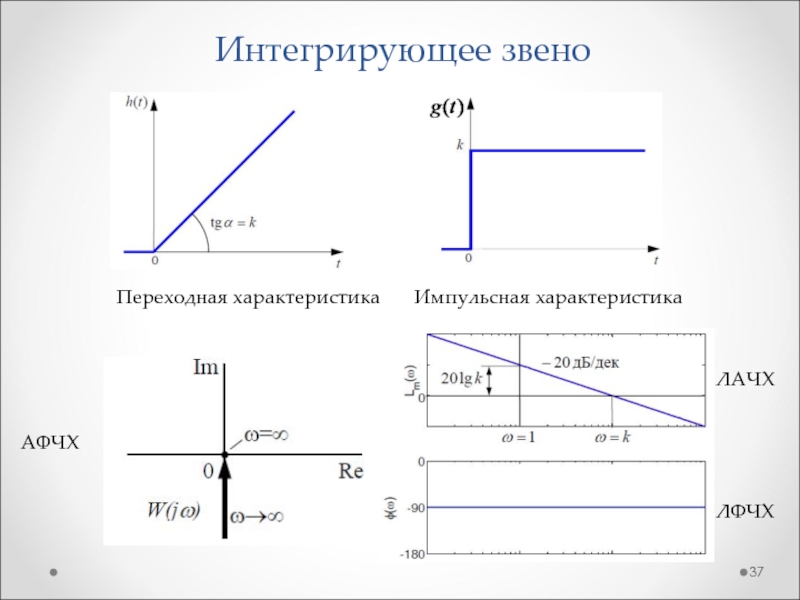
Слайд 36Интегрирующее звено
- Передаточная функция
- Переходная характеристика
- Импульсная характеристика
- АФЧХ
- ЛАЧХ
Слайд 38Идеально дифференцирующее звено
- Передаточная функция
- Переходная характеристика
- Импульсная характеристика
- АФЧХ
-
ЛАЧХ
Физически не реализуемое, так как звено реагирует не на изменение
самой входной величины, а на изменение ее производной, то есть на тенденцию развития событий.Слайд 40Форсирующее звено
- Передаточная функция
- Переходная характеристика
Физически не реализуемое
- АФЧХ
- ЛАЧХ
Слайд 42Построение ЛАЧХ
Рассмотрим звено второго порядка с передаточной функцией:
1)Представим данную
передаточную функцию в виде произведения
2)Согласно первому свойству ЛАЧХ, получим:
3)Определяем
сопрягающие частоты. Частоты на, которых «подключаются» соответствующие звенья.Слайд 44Структурное преобразование схем
Разветвление сигнала:
Параллельное и последовательное соединение звеньев:
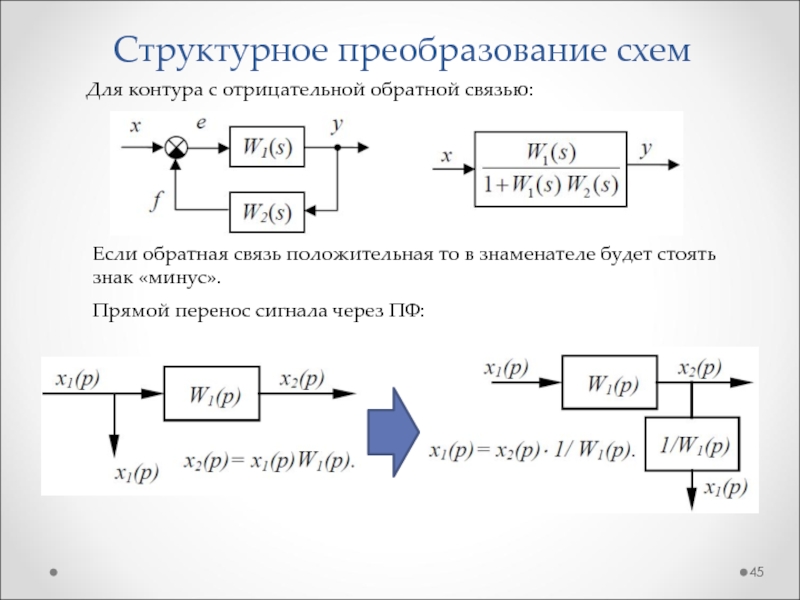
Слайд 45Структурное преобразование схем
Для контура с отрицательной обратной связью:
Если обратная
связь положительная то в знаменателе будет стоять знак «минус».
Прямой
перенос сигнала через ПФ: Слайд 46Структурное преобразование схем
Прямой перенос суммирующего звена:
Обратный перенос сигнала через
ПФ:
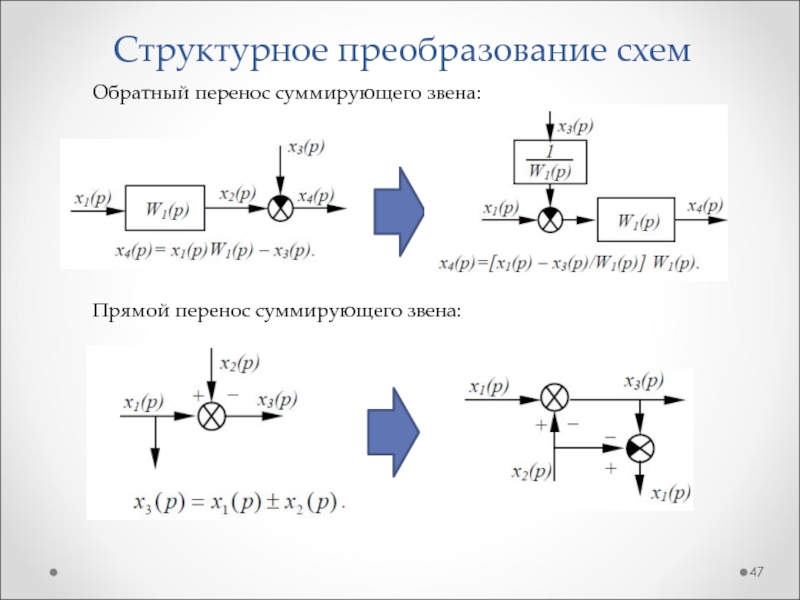
Слайд 47Структурное преобразование схем
Прямой перенос суммирующего звена:
Обратный перенос суммирующего звена:
Слайд 48Передаточные функции систем
Передаточная функция по возмущающему воздействию:
Передаточная функция по
управлению
Передаточная функция по рассогласованию:
Слайд 51Критерии устойчивости
(критерий Гурвица)
Пример для полинома пятого порядка (n=5):
Все корни полинома
Δ(s) имеют отрицательные вещественные части тогда и только тогда, когда
все n главных миноров матрицы Hn (определителей Гурвица) положительны.Характеристическое уравнение замкнутой САУ: