Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теория экономического анализа презентация
Содержание
- 1. Теория экономического анализа презентация
- 2. Слайд 2
- 3. Слайд 3
- 4. Слайд 4
- 5. Методы сравнительного
- 6. Виды сравнительного анализаГоризонтальный используется для определения абсолютных
- 7. Экономические показателиЭкономические явления и процессы выражаются обычно
- 8. Вертикальный анализ
- 9. Удельные показатели являются относительными, производными от соответствующих
- 10. Абсолютный прирост – это разность
- 11. Относительными показателями также являются темпы роста и
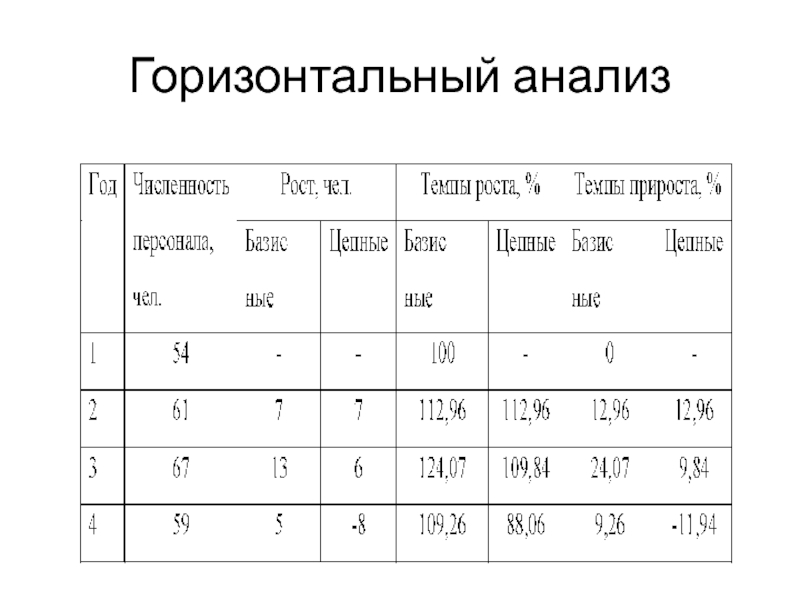
- 12. Горизонтальный анализ
- 13. Слайд 13
- 14. Виды факторных моделейАддитивные. Значение анализируемого показателя определяется
- 15. Мультипликативные. Значение анализируемого показателя определяется как произведение
- 16. Кратные. Значение анализируемого показателя определяется как частное
- 17. Смешанные. Такие модели могут иметь разную форму
- 18. К классу кратных моделей применяют следующие способы их преобразования: удлинения,формального разложения, расширениясокращения.
- 19. Способ удлинения предусматривает удлинение числителя исходной модели
- 20. Способ формального разложения факторной системы предусматривает удлинение
- 21. Метод расширения предусматривает расширение исходной факторной модели
- 22. Способ сокращения представляет собой создание новой факторной
- 23. Способы расчёта факторных моделейВ детерминированном анализе для
- 24. Правила построения факторных моделейправила, определяющие последовательность подстановки:-
- 25. Под количественным факторами при анализе понимают те,
- 26. Способ цепной подстановки Поскольку при
- 27. Порядок определения влияния факторовОбщий алгоритм определения влияния
- 28. В кратных моделях типа Y =
- 29. Методика расчета влияния факторов в смешанных моделях.
- 30. б) кратно-аддитивного типа Y = А /
- 31. Способ абсолютных разницАлгоритм расчета факторов на величину
- 32. Способ относительных разницСпособ относительных разниц также является
- 33. сначала находят относительное отклонение каждого факторного показателя
- 34. определяют отклонение результативного показателя Y за счет
- 35. Алгоритм расчета факторов на величину исследуемого результативного
- 36. Интегральный способ. Модель вида Y = А
- 37. Логарифмический способАлгоритм расчета факторов на величину исследуемого
- 38. Слайд 38
- 39. Скачать презентанцию
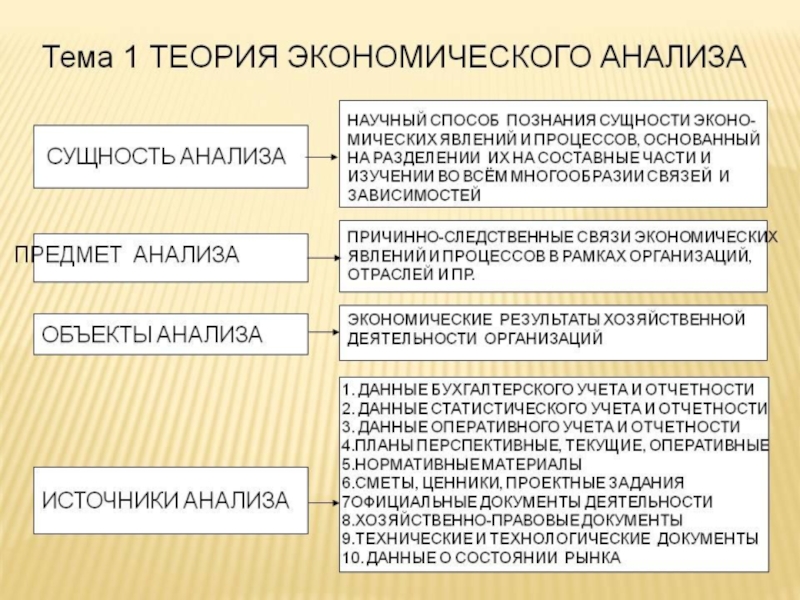
Методы сравнительного анализа . Сравнение – это научный метод познания, в процессе его неизвестное (изучаемое) явление, предметы сопоставляются с уже известными, изучаемыми ранее, с
Слайды и текст этой презентации
Слайд 6Виды сравнительного анализа
Горизонтальный используется для определения абсолютных и относительных отклонений
фактического уровня исследуемых показателей от базового (планового, прошлого периода, среднего
уровня, достижений науки и передового опыта).Вертикальный – изучается структура экономических явлений и процессов путем расчета удельного веса частей в общем целом (например, удельный вес постоянных затрат в себестоимости), соотношения частей целого между собой (например, постоянных и переменных затрат), а также влияния факторов на уровень результативных показателей путем сравнения их величины до и после изменения соответствующего фактора.
Трендовый анализ применяется при изучении относительных темпов роста и прироста показателей за ряд лет к уровню базисного года, т.е. при исследовании рядов динамики.
Слайд 7Экономические показатели
Экономические явления и процессы выражаются обычно в абсолютных и
относительных показателях.
Абсолютный показатель характеризует количественные размеры явления безотносительно к
размеру других явлений. Относительные показатели отражают соотношение величины изучаемого явления с величиной других явлений или с величиной этого явления, но взятой за другой период времени. Относительный показатель получают делением одной величины на другую.Относительные величины представляют собой частное от деления одного абсолютного числа на другое. Если разделить текущее значение показателя на базисное, мы получим простое отношение, называемое часто коэффициентом и показывающее, во сколько раз первое число больше второго. Умножив частное на 100, получим процентное отношение.
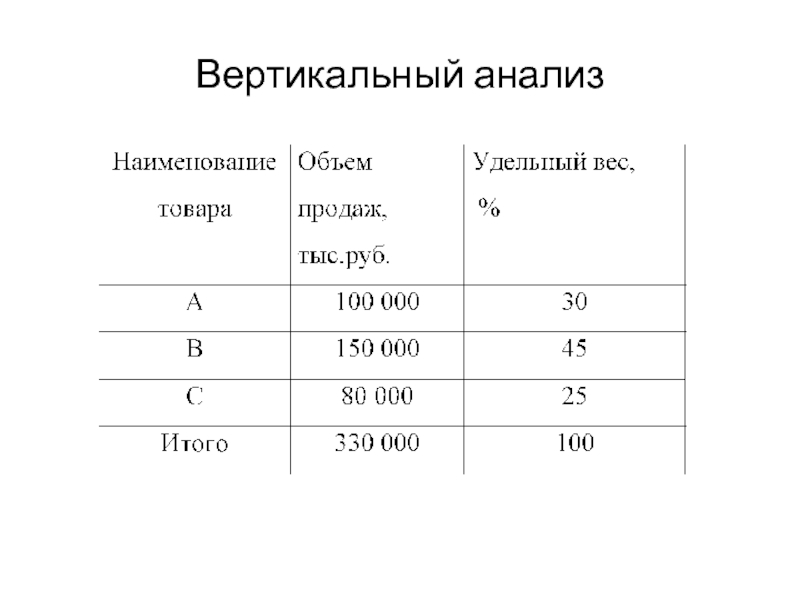
Слайд 9Удельные показатели являются относительными, производными от соответствующих объемных показателей. Удельными
показателями можно считать: выработку на одного работника, товарные запасы в
днях оборота, уровень издержек на рубль продаж и др. Широко применяются в экономических расчетах и другие относительные величины, характеризующие выполнение плана, структуру, динамику, интенсивность развития.Показатель структуры (удельный вес) - показывает относительную долю составного элемента в общей сумме
Слайд 10
Абсолютный прирост – это разность между последующим и предыдущим значениями
показателя (цепные) или начальным значением (базисные). Цепной абсолютный прирост характеризует
последовательное изменение показателей, а базисный абсолютный прирост – изменение нарастающим итогом. Абсолютный прирост показывает, на сколько абсолютных единиц изменился данный уровень по сравнению:а) с предыдущим уровнем при цепном способе;
б) с начальным уровнем при базисном способе.
Слайд 11Относительными показателями также являются темпы роста и прироста, характеризующие динамику
изменения показателя.
Темп роста – это отношение последующего значения показателя
к предыдущему (цепные темпы роста) или постоянному, принятому за базу сравнения (базисные темпы роста):Цепной способ характеризует последовательное изменение, а базисный способ – изменение нарастающим итогом
Слайд 14Виды факторных моделей
Аддитивные. Значение анализируемого показателя определяется как сумма показателей-факторов.
Такая модель имеет вид
Y = А + В + С.
Примером
аддитивной модели может быть балансовая прибыль предприятия, которая складывается из таких составляющих, как прибыль от реализации, результат от участия в деятельности других предприятий и сальдо прочих доходов и расходов. Слайд 15Мультипликативные. Значение анализируемого показателя определяется как произведение показателей - факторов.
Такая модель имеет вид
Y = А * В * С.
Большинство
моделей, используемых в факторном анализе - мультипликативные. Например, выручку можно представить как произведение количество продукции на стоимость единицы продукции. Суммарные материальные затраты предприятия - произведение трех факторов - количество произведенной продукции, норма расхода материала на единицу продукции, стоимость единицы материальных ресурсов. Слайд 16Кратные. Значение анализируемого показателя определяется как частное от деления двух
факторов. Такая модель имеет вид
Y = А / В.
В качестве
примера можно привести показатель фондовооруженности, определяемый делением стоимости основных средств на численность работающих. Слайд 17Смешанные. Такие модели могут иметь разную форму и представлять собой
различные комбинации аддитивных, мультипликативных и кратных моделей:
Y = А *
(В + С);Y = А / (В + С);
Y= (А / В) * С.
Примером такой модели может быть определение фонда оплаты труда как произведения средней заработной платы и численности. При этом средняя заработная плата представляет собой сумму нескольких составляющих - тарифной составляющей, доплат стимулирующего характера и доплат компенсирующего характера:
ФОТ = ( ЗП тар + ЗП стим + ЗП комп) * Ч.
Слайд 18К классу кратных моделей применяют следующие способы их преобразования:
удлинения,
формального
разложения,
расширения
сокращения.
Слайд 19Способ удлинения предусматривает удлинение числителя исходной модели путем замены одного
или нескольких факторов на сумму однородных показателей. Например, себестоимость единицы
продукции можно представить в качестве функции двух факторов: изменения суммы затрат (З) и объема выпуска продукции (VВП). Исходная модель этой факторной системы будет иметь видЕсли общую сумму затрат (З) заменить отдельными их элементами, такими, как заработная плата (ЗП), сырье и материалы (СМ), амортизация основных средств (А), накладные расходы (НР) и др., то детерминированная факторная модель будет иметь вид аддитивной модели с новым набором факторов:
X1 + X2 + X3 + X4,
где X1 – трудоемкость продукции; X2 – материалоемкость продукции; X3 – фондоемкость продукции; X4 – уровень накладных расходов.
Слайд 20Способ формального разложения факторной системы предусматривает удлинение знаменателя исходной факторной
модели путем замены одного или нескольких факторов на сумму или
произведение однородных показателей.Например, рентабельность можно представить в качестве функции двух факторов: изменения суммы прибыли от реализации продукции (П) и суммы затрат на производство и реализацию продукции (З). Исходная модель этой факторной системы будет иметь вид
.
.
Если затрат (З) заменить на отдельные ее элементы, конечная модель в результате преобразования примет вид:
.
Слайд 21Метод расширения предусматривает расширение исходной факторной модели за счет умножения
числителя и знаменателя дроби на один или несколько новых показателей.
Например, если в исходную модельY = А / В
ввести новый показатель С, то модель примет вид:
Y =
Слайд 22Способ сокращения представляет собой создание новой факторной модели путем деления
числителя и знаменателя дроби на один и тот же показатель:
Слайд 23Способы расчёта факторных моделей
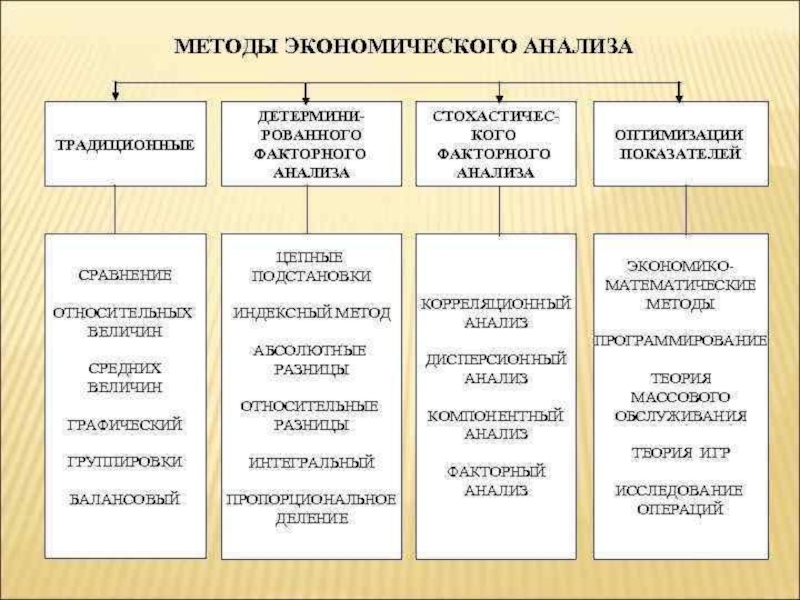
В детерминированном анализе для этого используются следующие
способы: цепной подстановки, индексный, абсолютных разниц, относительных разниц, пропорционального деления,
логарифмический и интегральный методы.Первых четыре способа основываются на методе элиминирования. Элиминировать - это значит устранить, отклонить, исключить воздействие всех факторов на величину результативного показателя кроме одного. Этот метод исходит из того, что все факторы изменяются независимо друг от друга: сначала изменяется один, а все другие остаются без изменения, потом изменяются два, затем три и т.д., при неизменности остальных. Это позволяет определить влияние каждого фактора на величину исследуемого показателя в отдельности.
Недостаток метода состоит в том, что, в зависимости от выбранного порядка замены факторов, результаты факторного разложения имеют разные значения. Это связано с тем, что в результате применения этого метода образуется некий неразложимый остаток, который прибавляется к величине влияния последнего фактора.
Слайд 24Правила построения факторных моделей
правила, определяющие последовательность подстановки:
- при наличии в
факторной модели количественных и качественных показателей в первую очередь рассматривается
изменение количественных факторов;- если модель представлена несколькими количественными и качественными показателями, то в первую очередь определяется влияние факторов первого порядка, затем второго и т.д.
Слайд 25Под количественным факторами при анализе понимают те, которые выражают количественную
определенность явлений и могут быть получены путем непосредственного учета (количество
рабочих, станков, сырья и т.д.).Качественные факторы определяют внутренние качества, признаки и особенности изучаемых явлений (производительность труда, качество продукции, себестоимость продукции, показатели рентабельности, фондоотдача, материалоотдача и т.д.).
Слайд 26Способ цепной подстановки
Поскольку при использовании способа цепной
подстановки применяется метод элиминирования, то следует придерживаться следующей последовательности расчетов:
в первую очередь нужно учитывать изменение количественных, а затем качественных показателей. Если же имеется несколько количественных и несколько качественных показателей, то сначала следует изменить величину факторов первого уровня подчинения, а потом более низкого.Данный способ используется для расчета влияния факторов во всех типах детерминированных факторных моделей: аддитивных, мультипликативных, кратных и смешанных.
Слайд 27Порядок определения влияния факторов
Общий алгоритм определения влияния факторов при использовании
этого способа в мультипликативной модели следующего вида Y = А
* В * С будет следующим:Yo = Ao* Bo* Co
Yусл 1 = А1*Во*Со
∆ YА = Yусл 1 - Yo
Yусл 2= А1*В1*Со
∆ YВ = Yусл 2 – Yусл. 1
Y1= А1*В1*С1
∆ YС = Y1 - Yусл 2
где Ao, Bo, Co – значения факторных показателей в базисном
( плановом ) периоде; А1, В1, С1 -
фактические значения факторных показателей в отчетном периоде.
Слайд 28В кратных моделях типа Y = А / В
алгоритм расчета факторов на величину исследуемого результативного показателя будет
следующий:Yо = Ао / Во
Yусл 1 = А1/ Во
∆ YА = Yусл 1 - Yo
Y1= А1/ В1
∆ YВ = Y1 – Yусл. 1
Слайд 29Методика расчета влияния факторов в смешанных моделях.
а) мультипликативно-аддитивного типа
Y = А * (В - С)
Yо = Ао *
(Во - Со)Yусл 1 = А1*(Во – Со)
∆ YА = Yусл 1 - Yo
Yусл 2= А1*(В1 – Со)
∆ YВ = Yусл 2 – Yусл. 1
Y1= А1*( В1 - С1)
∆ YС = Y1 - Yусл 2
Слайд 30б) кратно-аддитивного типа Y = А / (В +С)
Yо =
Ао /( Во+ Со)
Yусл 1 = А1/( Во+ Со)
∆ YА
= Yусл 1 - YoY усл1= А1/ (В1+ Со)
∆ YВ = Y1 – Yусл. 1
Y1= А1/( В1 + С1)
∆ YС = Y1 - Yусл 2
Слайд 31Способ абсолютных разниц
Алгоритм расчета факторов на величину исследуемого результативного показателя
при использовании способа абсолютных разниц для мультипликативной модели типа
Y = А * В * Сбудет следующий:
Yo = Ao* Bo* Co
∆ YА =∆А* Bo* Co
∆ YВ = A1* ∆B* Co
∆ YС = A1* B1* ∆C
∆Y общ = ∆ YА+∆ YВ + ∆ YС
Слайд 32Способ относительных разниц
Способ относительных разниц также является одной из модификацией
способа цепной подстановки. Применяется для измерения влияния факторов на прирост
результативного показателя в мультипликативных моделях. Он используется в случаях, когда исходные данные содержат определенные ранее относительные отклонения факторных показателей в процентах.Для мультипликативной модели типа Y = А * В * С методика факторного анализа будет следующей:
Слайд 33сначала находят относительное отклонение каждого факторного показателя в процентах
∆А%=
∆В%=
∆С%= Слайд 34определяют отклонение результативного показателя Y за счет каждого фактора
∆ YА =
∆ YВ =
∆ YС =
Слайд 35Алгоритм расчета факторов на величину исследуемого результативного показателя при использовании
индексного способа для мультипликативной модели типа Y =
А * В * С будет следующий:а) сначала определяются индексы изменения факторных показателей по следующим формулам:
IA = A1/A0 IB = B1/B0 IC = C1/C0
б) далее расчет влияния каждого из факторов определяется по формулам:
где Y0 – базисное изменение результативного показателя;
IA – индекс изменения факторного показателя А; IB - индекс изменения факторного показателя В; IC - индекс изменения факторного показателя С.
Слайд 37Логарифмический способ
Алгоритм расчета факторов на величину исследуемого результативного показателя при
использовании логарифмического способа для мультипликативной модели типа Y
= А * В будет следующий:Lg Y= lg A + lg В
а) влияние изменения фактора А на изменение результативного показателя
ΔYA= ΔY*
б) влияние изменения фактора А на изменение результативного показателя
ΔYB= ΔY*
Общее изменение: ΔYобщ=Y1-Y0= ΔYA + ΔYВ