Слайд 2Актуальность
В конфликтных ситуациях, когда две или более оперирующие стороны преследуют
несовпадающие цели, значение целевой функции каждой стороны зависит не только
от решения, выбранного данной стороной, но и от решений, выбранных другими сторонами
Раздел исследования операций, ориентированный на разработку методов выбора оптимальных решений учитывающих решения, принимаемые каждой из сторон, участвующих в операции, называется теорией игр
Слайд 3Области применения теории игр
- экономика;
- политика;
- военные
действия и т. д.
Слайд 4Основные понятия
Конфликтная ситуация – это столкновение интересов двух или более
сторон.
Игра – это математическая модель конфликтных ситуаций, а также система
предварительно оговоренных правил и условий.
Партией называется частичная реализация правил и условий игры. Результатом игры всегда является число v, которое называется выигрышем, проигрышем или ничьей.
если υ > 0 – выигрыш
если υ < 0 – проигрыш
если υ = 0 – ничья
Слайд 5КЛАССИФИКАЦИЯ ИГР
По числу игроков:
игры одного игрока, двух игроков,
n игроков
По
количеству стратегий:
конечные и бесконечные
По характеру взаимоотношений:
бескоалиционные, коалиционные и кооперативные
По характеру
выигрышей:
с нулевой суммой и
игры с ненулевой суммой
По виду функций выигрышей:
матричные, биматричные, непрерывные,
выпуклые, сепарабельные, типа дуэлей и др.
По количеству шагов:
одношаговые и многошаговые
Слайд 6Основные понятия. Стратегии
Стратегией игрока называется совокупность правил, определяющих выбор варианта
действий при каждом личном ходе в зависимости от сложившейся ситуации.
В зависимости от стратегий игры делятся на конечные и бесконечные.
Игра называется конечной, если у каждого игрока имеется в распоряжении только конечное число стратегий (в противном случае игра называется бесконечной).
Процесс игры состоит в выборе каждым игроком одной своей стратегии
В результате каждой партии игры складывается система стратегий
s = (s1, s2,…, sn), которая называется ситуацией
Множество всех ситуаций обозначается S = S1, S2, …, Sn и представляет собой декартово произведение множеств, стратегий всех игроков
Слайд 7Наш пример
Игра с нулевой суммой – это игра, в которой
сумма выигрышей игроков равна нулю (т.е. каждый игрок выигрывает только
за счет других). Самый простой случай – парная игра с нулевой суммой – антагонистическая игра, здесь два игрока четко играют друг против друга.
Число игроков обозначим I, I=(1, 2, …, n).
Бескоалиционной игрой называется система , в которой число игроков I и стратегии игрока Si являются множествами, а платежная функция Hi – функция на множестве S, принимающая вещественные значения
Игра с нулевой суммой:
Слайд 8Понятие «антагонистическая игра»
Игра
называется антагонистической, если число игроков
в ней равно 2, а значения функций выигрышей этих игроков
в каждой ситуации равны по величине и противоположны по знаку
Следовательно, антагонистическая игра также является игрой с нулевой суммой
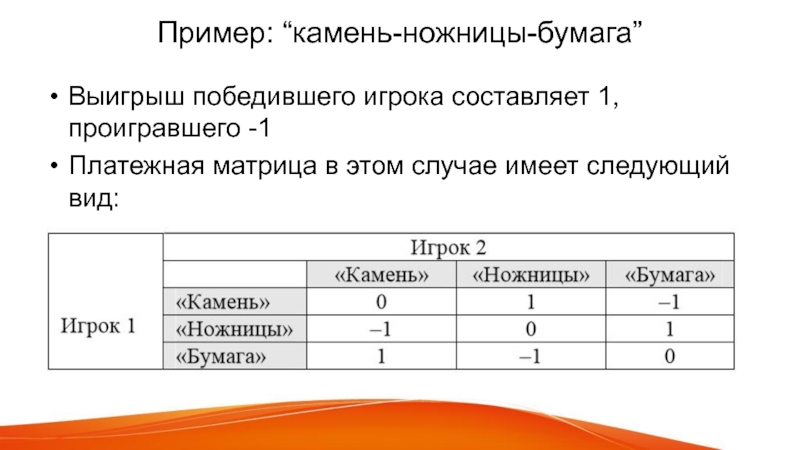
Слайд 10Пример: “камень-ножницы-бумага”
Выигрыш победившего игрока составляет 1, проигравшего -1
Платежная матрица в
этом случае имеет следующий вид:
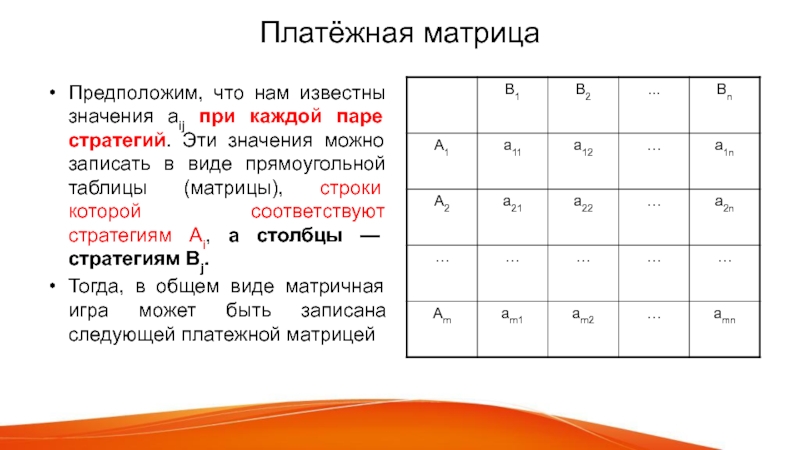
Слайд 11Платёжная матрица
Предположим, что нам известны значения aij при каждой паре
стратегий. Эти значения можно записать в виде прямоугольной таблицы (матрицы),
строки которой соответствуют стратегиям Ai, а столбцы — стратегиям Bj.
Тогда, в общем виде матричная игра может быть записана следующей платежной матрицей
Слайд 12Максиминные, минимаксные стратегии
Нижней чистой ценой игры называется
Верхней чистой ценой игры называется
Игра, для которой
, называется игрой с седловой точкой, где называется ценой игры.
Задача теории игр – поиск оптимальных стратегий (решений).
Решением игры называется пара оптимальных стратегий для игроков А и В, значение цены игры.
Наличие седловой точки означает наличие равновесия в игре.
Слайд 13ИГРА В МАТРИЧНОЙ ФОРМЕ
Стратегии игроков:
Платежная матрица:
Нижняя цена игры:
Верхняя цена
игры:
Условие существования
седловой точки:
Слайд 14Антагонистическая игра:
– множество стратегий первого игрока,
– множество
стратегий второго игрока,
– платежная функция или функция выигрыша.
Определение.
Пару называют седловой точкой
функции на , если
или
Графическая интерпретация
седловой точки:
Слайд 15- оценка эффективности стратегии x первого игрока, или гарантированный результат
Определение
эффективных стратегий
- наилучший гарантированный результат для первого игрока (нижняя цена
игры)
- максиминная стратегия первого игрока, если
- оценка эффективности стратегии y второго игрока, или гарантированный результат
- наилучший гарантированный результат для второго игрока (верхняя цена игры)
- минимаксная стратегия второго игрока, если
Слайд 16Теорема. 1) Для того, чтобы функция
на
имела
седловую точку, необходимо и достаточно, чтобы было
выполнено равенство
2) Пусть выполнено равенство (1). Пара тогда и только
тогда является седловой точкой, когда максиминная,
а – минимаксная стратегии первого и второго игроков
соответственно.
Справедливо неравенство:
Слайд 17
Чистые и смешанные стратегии
!!! Чистой стратегией
называют ход, выбранный с вероятностью 1.
Смешанной
стратегией игрока А называется вектор
.
Смешанной стратегией игрока В называется вектор
платежная функция.
чистая стратегия
Пара стратегий называется оптимальной, если
Слайд 18Активные стратегии
Активной стратегией называется стратегия, входящая в оптимальную смешанную стратегию
с ненулевой вероятностью.
Слайд 19Решение матричной игры 22
аналитический метод решения
Слайд 20Геометрическая интерпретация игры 22
Пусть имеется два игрока А и В.
У каждого из игроков по две стратегии (А1 и А2
у игрока А, В1 и В2 у игрока В). Игра с нулевой суммой.
По оси абсцисс отложим отрезок А1А2, то есть точка А1 изображает стратегию А1 (х=0), А2 – стратегию А2, все промежуточные точки – смешанные стратегии. На оси ординат откладываем выигрыш первого игрока, если второй применил стратегию В1. Аналогично строим второй график, если второй график выбрал стратегию В2.
Слайд 21 q1=a11p1+a21p2
q2=a12p1+a22p2
(ордината точки
М1 и М2, соответственно)
В соответствии с принципом минимакса оптимальная стратегия SА* такова, что минимальный выигрыш игрока А (при наихудшем поведении игрока В) обращается в максимум.
Слайд 22Решение игры графическим способом
Отрезок В1N – минимальный выигрыш игрока А
при использовании любой смешанной стратегии,
если игрок В выбрал стратегию
В1. Аналогично, отрезок В2N – выигрыш игрока А,
если игрок В выбрал стратегию В2.
Следовательно, оптимальную стратегию определяет точка N, то есть минимальный выигрыш достигает максимума
Слайд 27Пояснение
приравниваем v1=v4
4-8x= -1+3x; 11x=5; x=5/11
1-x= 1-5/11= 6/11
v= -1+3x = -1+3*(5/11)=
4/11
a11=4; a12= -1; v=4/11; подставляем в формулу, получаем q1=3/11. Аналогично
q4=8/11.
q2 и q3 = 0, поскольку эти столбцы не соответствуют точке перечения v1=v4