Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теория статистических решений (Статистические игры, игры с природой)
Содержание
- 1. Теория статистических решений (Статистические игры, игры с природой)
- 2. Тема 3. Статистические игры c единичным экспериментом Постановка задачи Подходы к решению
- 3. 3. Игра c единичным экспериментом. 3.1.
- 4. 3. Игра c единичным экспериментом. 3.1
- 5. 3. Игра c единичным экспериментом. 3.1.
- 6. 3. Игра c единичным экспериментом. 3.1.
- 7. 3. Игра c единичным экспериментом. 3.1.
- 8. 3. Игра c единичным экспериментом.
- 9. 3. Игра c единичным экспериментом.
- 10. 3. Игра c единичным экспериментом.
- 11. 3. Игра c единичным экспериментом.
- 12. 3. Игра c единичным экспериментом.
- 13. 3. Игра c единичным экспериментом.
- 14. 3. Игра c единичным экспериментом.
- 15. 3. Игра c единичным экспериментом.
- 16. Игра c единичным экспериментом. Подходы
- 17. 3. Игра c единичным экспериментом.
- 18. 3. Игра c единичным экспериментом.
- 19. 3. Игра c единичным экспериментом.
- 20. 3. Игра c единичным экспериментом.
- 21. 3. Игра c единичным экспериментом.
- 22. Скачать презентанцию
Слайды и текст этой презентации
Слайд 33. Игра c единичным экспериментом.
3.1. Постановка задачи. Слайд 1
ДАНО
(блоки данных: B+B’+C+C’)
Блок данных C:
e1 – единичный эксперимент
с(e1) –
стоимость экспериментаZ = {z1,z2,…za} – множество исходов эксперимента
P{z/s} – распределение условных вероятностей исходов эксперимента при том или ином состоянии «природы», т.е P(zl/sj),
l=1, … , a ; j=1, … , n
ПРИМЕР:
e1 – звонок в метеослужбу
с(e1) = 5
z1 – будет дождь
z2 – возможны осадки
z3 – будет ясно
P(zl/sj) =
=
Слайд 43. Игра c единичным экспериментом.
3.1 Постановка задачи. Слайд 2
Блок
данных C (продолжение):
!!! Возможные решения задачи представляются в виде
решающих функций вида:φk (z,d) : φk (zl) = di , k=1,w
НАЙТИ: решение задачи в виде решающей функции, т.е. найти способ поведения в зависимости от результата эксперимента
ПРИМЕР:
φ1 = { (1,2), (2,2),(3,1) },
т.е. φ1 (z1) = d2
и т.д.
φ2 = { (1,2), (2,1),(3,1) },
φ3 = { (1,1), (2,1),(3,1) }
Выпишите ВСЕ варианты решающих функций !
Слайд 53. Игра c единичным экспериментом.
3.1. Постановка задачи. Слайд 3
ДООПРЕДЕЛЕНИЕ
задачи (блок С’) :
Функция риска – математическое ожидание потерь в
случае выбора той или иной решающей функции при определенном состоянии «природы»R(φ,s) = ML (φ,s) = ∑L(φk (zl, di) *P(zl/sj)
z
R(φk, sj) =
= ∑L(φk (zl) = di ; sj) * P(zl / sj)
l
ПРИМЕР:
R(φ,s) =
Слайд 63. Игра c единичным экспериментом.
3.1. Постановка задачи. Слайд 4
ДООПРЕДЕЛЕНИЕ
задачи (блок С’) :
R(φk, sj) = ∑L(φk (zl) = di
; sj) * P(zl / sj)l
ПРИМЕР:
R(φ1,s1) = L [φ1(z1)=d2; s1] * P(z1/s1) +
+ L [φ1(z2)=d2; s1] * P(z2/s1) +
+ L [φ1(z3)=d1; s1] * P(z3/s1) =
= (-50)*0,5 + (-50)*0,4 + 100*0,1 = (- 25) + (- 20) + 10 = - 35
Слайд 73. Игра c единичным экспериментом.
3.1. Постановка задачи. Слайд 5
ДООПРЕДЕЛЕНИЕ
задачи (блок С’) :
R(φk, sj) = ∑L(φk (zl) = di
; sj) * P(zl / sj)l
ПРИМЕР:
R(φ1,s1) = L [φ1(z1)=d2; s1] * P(z1/s1) +
+ L [φ1(z2)=d2; s1] * P(z2/s1) +
+ L [φ1(z3)=d1; s1] * P(z3/s1) =
= (-50)*0,5 + (-50)*0,4 + 100*0,1 = (- 25) + (- 20) + 10 = - 35
Слайд 83. Игра c единичным экспериментом. 3.2. Подходы к решению
задачи. Слайд 1
Принцип минимакса
φ *(z) : R(φ*) =
=
min max R (φ,s) φ s
ПРИМЕР :
φ*(z) = φ1
и
φ*(z) = φ2
R(φ*) = 25
Слайд 93. Игра c единичным экспериментом. 3.2. Подходы к решению
задачи. Слайд 2
Принцип минимального ожидаемого риска
φ * : R(φ*)
= min MR (φ), φ где MR (φk) = ∑ R(φ,s) * P(s),
s
т.е.: MR (φk) =∑R(φ k,sj) * P(sj)
j
ПРИМЕР :
φ*(z) = φ1
R(φ*) = 7
Слайд 103. Игра c единичным экспериментом. 3.2. Подходы к решению
задачи . Слайд 3
принципы, основанные на использовании апостериорных вероятностей
ДООПРЕДЕЛЕНИЕ
задачи:Блок D’ – расчет апостериорных вероятностей
Слайд 113. Игра c единичным экспериментом. 3.2. Подходы к решению
задачи . Слайд 4
ДООПРЕДЕЛЕНИЕ задачи:
Блок D1 – расчет апостериорных
вероятностей ПРИМЕР
Слайд 123. Игра c единичным экспериментом. 3.2. Подходы к решению
задачи. Слайд 5
ДООПРЕДЕЛЕНИЕ задачи:
Блок D1 – расчет апостериорных вероятностей
ПРИМЕР :
P(z1) = P(z1/s1)*P(s1) + P(z1/s2)*P(s2) =
= 0,5 * 0,3 + 0,1 * 0,7 = 0,15 + 0,07 = 0,22
P(s2/z1) = [P(z1/s2) * P(s2)] / P(z1) =
= 0,1 * 0,7 / 0,22 = 0,32
P(s1/z1) = [P(z1/s1) * P(s1)] / P(z1) =
= 0,5 * 0,3 / 0,22 = 0,68
P(s1/z1) + P(s2/z1) = 1,0 !!
Слайд 133. Игра c единичным экспериментом. 3.2. Подходы к решению
задачи. Слайд 6
ДООПРЕДЕЛЕНИЕ задачи:
Блок D1 – расчет апостериорных вероятностей
ПРИМЕР (результаты расчета):
Примечание:
Неопределенность относительно
состояний природы может уменьшится,
а может увеличиться!
Слайд 143. Игра c единичным экспериментом. 3.2. Подходы к решению
задачи. Слайд 7
принципы, основанные на использовании апостериорных вероятностей
ДООПРЕДЕЛЕНИЕ задачи:
Блок D2 – расчет ожидаемых потерь на основе апостериорных вероятностейML^( d, z ) = ∑ L(d, s) * P (s / z)
s
ML^( di, zk) = ∑ L(di, sj) * P (sj / zk)
j
где ML^( d, z ) - ожидаемые потери, рассчитанные на основе апостериорных вероятностей
Слайд 153. Игра c единичным экспериментом. 3.2. Подходы к решению
задачи. Слайд 8
ДООПРЕДЕЛЕНИЕ задачи:
Блок D2 – расчет ожидаемых потерь на
основе апостериорных вероятностей ML^( di, zk) = ∑ L(di, sj) * P (sj / zk)
j
ПРИМЕР :
Слайд 16Игра c единичным экспериментом. Подходы к решению задачи -
9
ДООПРЕДЕЛЕНИЕ задачи:
Блок D2 – расчет ожидаемых потерь на основе апостериорных
вероятностей ML^( di, zk) = ∑ L(di, sj) * P (sj / zk)
j
ПРИМЕР :
ML^( d1, z3) = L(d1, s1) * P (s1 / z3) +
+ L(d1, s2) * P (s2 / z3) =
= 100 * 0,08 + 0 * 0,92 = 8
Слайд 173. Игра c единичным экспериментом. 3.2. Подходы к решению
задачи. Слайд 10
ДООПРЕДЕЛЕНИЕ задачи:
Блок D2 – расчет ожидаемых потерь на
основе апостериорных вероятностей ML^( di, zk) = ∑ L(di, sj) * P (sj / zk)
j
ПРИМЕР (результаты расчета):
Слайд 183. Игра c единичным экспериментом. 3.2. Подходы к решению
задачи. Слайд 11
принципы, основанные на использовании апостериорных вероятностей:
- Принцип
максимального правдоподобия- Байесовский принцип – принцип минималь-ного ожидаемого риска, рассчитанного на основе знания апостериорных вероятностей
Слайд 193. Игра c единичным экспериментом. 3.2. Подходы к решению
задачи. Слайд 12
Принцип максимального правдоподобия:
на основе каждого исхода
эксперимента делаются выводы о возможном состоянии природы в соответствии с наибольшей условной вероятностью P(s,z)При построении решающей функции учитываются наиболее вероятные состояния природы
Слайд 203. Игра c единичным экспериментом. 3.2. Подходы к решению
задачи. Слайд 13
Принцип максимального правдоподобия:
ПРИМЕР :
P(s/z) s1 s2
max наиболее вероятное состояниеz1 0,68 0,32 0,68 s1 – будет дождь
z2 0,30 0,70 0,70 s2 – будет ясно
z3 0,08 0,92 0,92 s2 – будет ясно
Отсюда решающая функция: z1 → d2 (т.к. будет дождь),
z2 → d1 (т.к. будет ясно),
z3 → d1 (т.к. будет ясно)
т.е φ*(z) = φ2 = {(1,2), (2,1), (3,1)} – оптимистическая стратегия
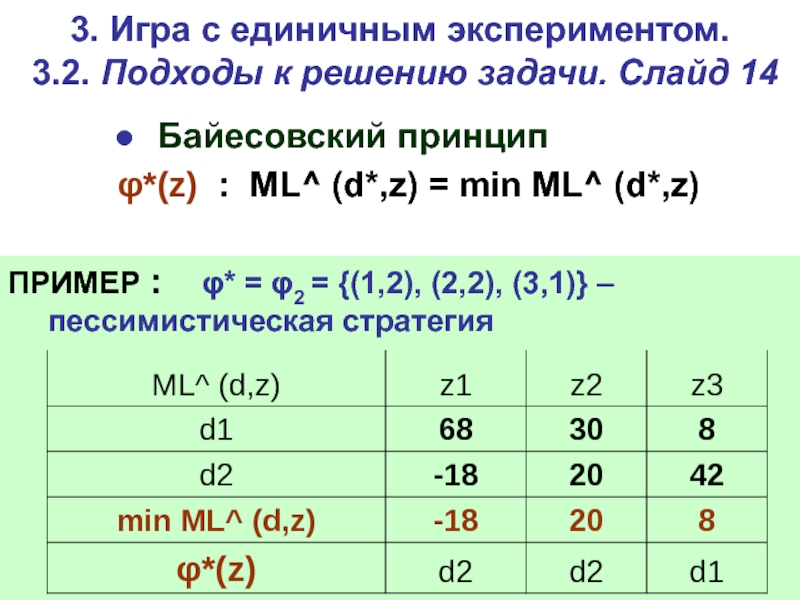
Слайд 213. Игра c единичным экспериментом. 3.2. Подходы к решению
задачи. Слайд 14
Байесовский принцип
φ*(z) : ML^ (d*,z) = min
ML^ (d*,z)ПРИМЕР : φ* = φ2 = {(1,2), (2,2), (3,1)} –пессимистическая стратегия