Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теория информации Энтропия непрерывного источника сообщений Лекция 5. Энтропия
Содержание
- 1. Теория информации Энтропия непрерывного источника сообщений Лекция 5. Энтропия
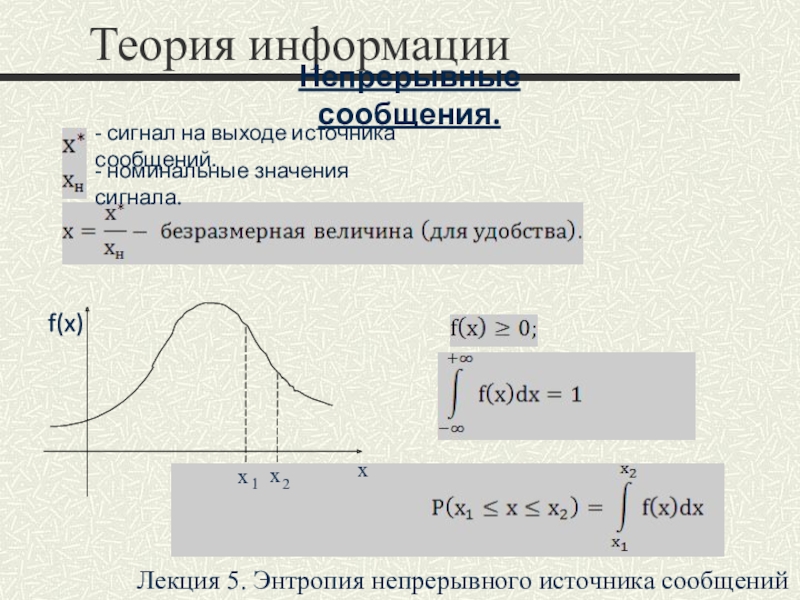
- 2. Теория информацииЛекция 5. Энтропия непрерывного источника сообщенийНепрерывные сообщения.- сигнал на выходе источника сообщений.- номинальные значения сигнала.f(x)хх1х2
- 3. Теория информацииЛекция 5. Энтропия непрерывного источника сообщений1.
- 4. Теория информацииЛекция 5. Энтропия непрерывного источника сообщений1. Энтропия источника сообщений после квантования.1
- 5. Теория информацииЛекция 5. Энтропия непрерывного источника сообщенийf(x)3.
- 6. Теория информацииЛекция 5. Энтропия непрерывного источника сообщенийВзаимная
- 7. Теория информацииЛекция 5. Энтропия непрерывного источника сообщений1.
- 8. Теория информацииЛекция 5. Энтропия непрерывного источника сообщенийСредняя взаимная информация.
- 9. Теория информацииЛекция 5. Энтропия непрерывного источника сообщенийФункциона́л — числовая
- 10. Виды функционаловинтегральный: терминальный: смешанный (функционал Больца): Теория информацииЛекция 5. Энтропия непрерывного источника сообщений
- 11. Теория информацииЛекция 5. Энтропия непрерывного источника сообщенийВариацио́нное
- 12. Теория информацииЛекция 5. Энтропия непрерывного источника сообщенийТермин варьирование (варьировать)
- 13. Теория информацииЛекция 5. Энтропия непрерывного источника сообщенийЕщё
- 14. Основные задачи вариационного исчисления:нахождение точек в пространстве функций, на
- 15. Теория информацииЛекция 5. Энтропия непрерывного источника сообщенийУсловным
- 16. Основные виды задачи на условный экстремум, которые
- 17. Для нахождения условного экстремума
- 18. Теория информацииЛекция 5. Энтропия непрерывного источника сообщенийКлючевым
- 19. Теория информацииЛекция 5. Энтропия непрерывного источника сообщенийМаксимум
- 20. Теория информацииЛекция 5. Энтропия непрерывного источника сообщенийУсловие
- 21. Теория информацииЛекция 5. Энтропия непрерывного источника сообщенийРешение:
- 22. Теория информацииЛекция 5. Энтропия непрерывного источника сообщенийЗадача
- 23. Теория информацииЛекция 5. Энтропия непрерывного источника сообщенийРешение:
- 24. Теория информацииЛекция 5. Энтропия непрерывного источника сообщенийОткуда:
- 25. Теория информацииЛекция 5. Энтропия непрерывного источника сообщенийГауссовский
- 26. Теория информацииЛекция 5. Энтропия непрерывного источника сообщений3)
- 27. Теория информацииЛекция 5. Энтропия непрерывного источника сообщенийГауссовский
- 28. Теория информацииЛекция 5. Энтропия непрерывного источника сообщенийПомеха
- 29. Теория информацииЛекция 5. Энтропия непрерывного источника сообщенийТребуется
- 30. Теория информацииЛекция 5. Энтропия непрерывного источника сообщений=с
- 31. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Теория информации
Энтропия непрерывного источника сообщений
Лекция 5. Энтропия непрерывного источника сообщений
Слайд 2Теория информации
Лекция 5. Энтропия непрерывного источника сообщений
Непрерывные сообщения.
- сигнал на
выходе источника сообщений.
Слайд 3Теория информации
Лекция 5. Энтропия непрерывного источника сообщений
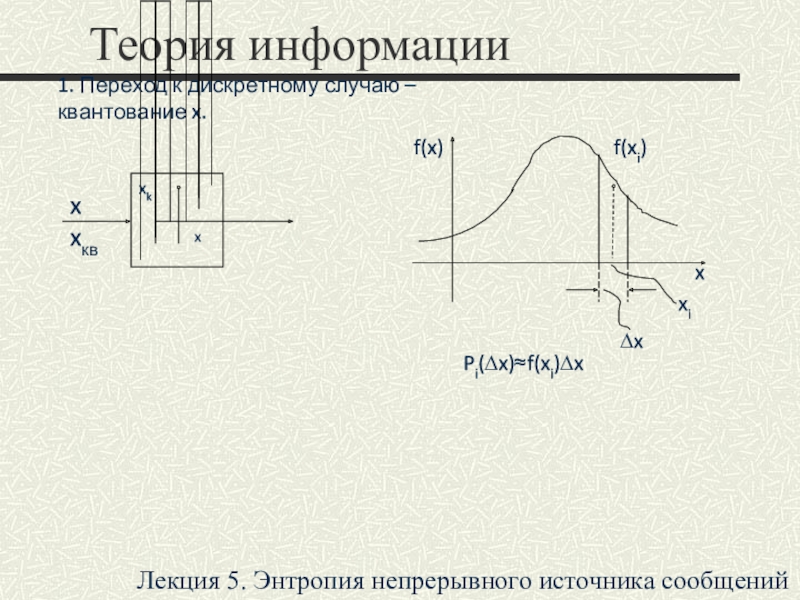
1. Переход к дискретному
случаю – квантование x.
x
xквx
∆x – шаг квантования
f(x)
f(xi)
x
∆x
xi
Pi(∆x)≈f(xi)∆x
Слайд 4Теория информации
Лекция 5. Энтропия непрерывного источника сообщений
1. Энтропия источника сообщений
после квантования.
1
Слайд 5Теория информации
Лекция 5. Энтропия непрерывного источника сообщений
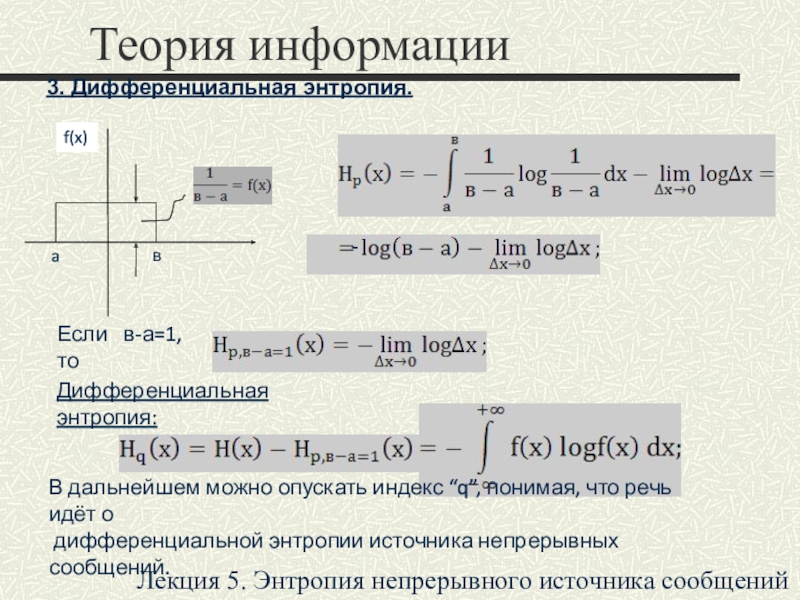
f(x)
3. Дифференциальная энтропия.
a
в
Если в-а=1, то
Дифференциальная энтропия:
В дальнейшем можно опускать индекс “q”, понимая, что речь идёт о
дифференциальной энтропии источника непрерывных сообщений.
-
Слайд 6Теория информации
Лекция 5. Энтропия непрерывного источника сообщений
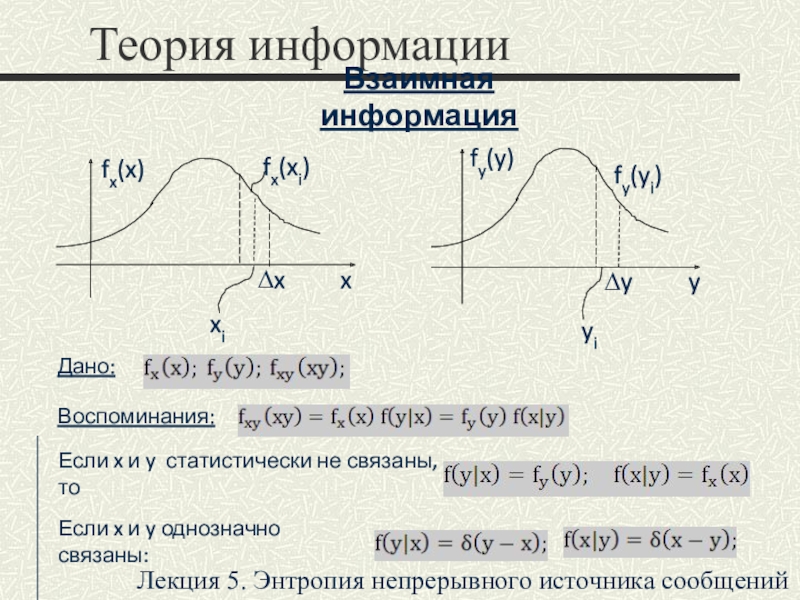
Взаимная информация
Дано:
Воспоминания:
Если x и y статистически не связаны, то
Если x
и y однозначно связаны:
Слайд 7Теория информации
Лекция 5. Энтропия непрерывного источника сообщений
1. Квантуем по уровню
x с шагом ∆x;
2. Квантуем по уровню y с шагом
∆y;4. Для дискретных (квантованных) сообщений:
3.
При ∆x→0 и ∆y→0 выражение
остаются теми же.
Слайд 8Теория информации
Лекция 5. Энтропия непрерывного источника сообщений
Средняя взаимная информация.
Слайд 9Теория информации
Лекция 5. Энтропия непрерывного источника сообщений
Функциона́л — числовая функция, заданная на
векторном пространстве. Функционал берёт в качестве аргумента элемент линейного пространства (вектор) и
возвращает в качестве результата скаляр. Довольно часто в роли линейного пространства выступает то или иное пространство функций (непрерывные функции на отрезке, интегрируемые функции на плоскости т. д. Неформально говоря, функционал — это функция от функций, переводящая функцию в число (действительное или комплексное).Самый простой функционал — проекция (сопоставление вектору одной из его координат).
Отображение, переводящее вектор в его норму.
Задачи оптимизации формулируются на языке функционалов: найти решение (уравнения, системы уравнений, системы ограничений, системы неравенств, системы включений и т. п.), доставляющее экстремум (минимум, максимум) заданному функционалу.
Слайд 10Виды функционалов
интегральный:
терминальный:
смешанный (функционал Больца):
Теория информации
Лекция 5. Энтропия
непрерывного источника сообщений
Слайд 11Теория информации
Лекция 5. Энтропия непрерывного источника сообщений
Вариацио́нное исчисле́ние — это раздел функционального
анализа, в котором изучаются вариации функционалов. Самая типичная задача вариационного исчисления состоит
в том, чтобы найти функцию, на которой заданный функционал достигает экстремальногозначения.
Слайд 12Теория информации
Лекция 5. Энтропия непрерывного источника сообщений
Термин варьирование (варьировать) применяется в вариационном
исчислении для обозначения нахождения вариации или вариационной производной.
Вариационная задача означает,
как правило, нахождение функции, удовлетворяющей условию стационарности некоторого заданного функционала, то есть такой функции, (бесконечно малые) возмущения которой не вызывают изменения функционала по крайней мере в первом порядке малости. Также вариационной задачей называют тесно связанную с этим задачу нахождения функции, на которой данный функционал достигает локального экстремума (во многом эта задача сводится к первой, иногда практически полностью). Типичными примерами вариационной задачи являются изопериметрические задачи в геометрии и механике; в физике — задача нахождения уравнений поля из заданного вида действия для этого поля.
Слайд 13Теория информации
Лекция 5. Энтропия непрерывного источника сообщений
Ещё в античные времена
появились первые вариационные проблемы, относящиеся к категории изопериметрических задач :
Из всех фигур
с заданным периметром наибольшую площадь имеет круг.Из всех многоугольников с заданным числом сторон и заданным периметром наибольшую площадь имеет правильный многоугольник.
Из всех тел с заданной площадью поверхности наибольший объём имеет шар.
Аналогом дифференциала (первого дифференциала) является в вариационном исчислении вариация (первая вариация):
Слайд 14Основные задачи вариационного исчисления:
нахождение точек в пространстве функций, на котором определён функционал — точек
стационарного функционала, стационарных функций, линий, траекторий, поверхностей и т. п., то есть нахождение для
заданного таких , для которых при любом (бесконечно малом) , или, иначе, где ,нахождение локальных экстремумов функционала, то есть в первую очередь определение тех , на которых принимает локально экстремальные - нахождение экстремалей(иногда также определение знака экстремума).
Теория информации
Лекция 5. Энтропия непрерывного источника сообщений
Слайд 15Теория информации
Лекция 5. Энтропия непрерывного источника сообщений
Условным экстремумом называется экстремум не
на всей области определения функции (функционала), а на определённом её
подмножестве, выделяемом специально наложенным условием (или условиями). Обычно, речь идёт о выделении этим условием (условиями) подмножества области определения с меньшей размерностью, что для конечномерных областей имеет определённый наглядный смысл, но для бесконечномерных (каковы обычно области определения функционалов) налагаемые условия приходится рассматривать лишь абстрактно (что теоретически не мешает иметь в виду полезную аналогию с конечномерным случаем)Слайд 16Основные виды задачи на условный экстремум, которые имеет смысл рассмотреть,
таковы:
Надо найти экстремум функционала при условии равенства
нулю другого функционала ; (то, что в правой части нуль, не нарушает общности).Надо найти экстремум функционала при условии
.
Надо найти экстремум функционала при условии выполнения для уравнения , где — некоторая функция и/или производных , обозначенных штрихами.
Теория информации
Лекция 5. Энтропия непрерывного источника сообщений
Слайд 17Для нахождения условного экстремума в первых двух
из перечисленных случаях применим метод неопределенных множителей Лагранжа. Нужно решить вариационную
задачу для функционала в первом и во втором случае, а затем подобрать (решив уравнение в первом случае и N уравнений с частными производными по каждому из во втором) такие , которые реализуют минимум в найденном семействе функций f, для которого эти являются параметрами.Теория информации
Лекция 5. Энтропия непрерывного источника сообщений
Слайд 18Теория информации
Лекция 5. Энтропия непрерывного источника сообщений
Ключевым моментом является нахождение
и приравнивание нулю вариации (или вариационной производной) для некоего нового
функционала , для этих двух случаев:Уравнения Эйлера — Лагранжа — дифференциальные уравнения, которым должна удовлетворять функция, на которой функционал достигает локального экстремума.
Слайд 19Теория информации
Лекция 5. Энтропия непрерывного источника сообщений
Максимум дифференциальной энтропии.
Задача 1.
Определить
максимум
Таким образом:
а≤x≤в;
при заданном диапазоне
случайнойвеличины X: а≤x≤в.
Воспоминания:
y(x)-неизвестная функция.
Слайд 20Теория информации
Лекция 5. Энтропия непрерывного источника сообщений
Условие
Требуется найти y(x), доставляющую
максимум (минимум) J.
Уравнение Эйлера:
Слайд 22Теория информации
Лекция 5. Энтропия непрерывного источника сообщений
Задача 2. Определить максимум
дифференциальной энтропии при
заданной мощности (дисперсии) сигнала.
Определить максимум
при
условии:Обратите внимание: диапазон не ограничен (1); математическое ожидание
принято равным 0 (2).
Слайд 25Теория информации
Лекция 5. Энтропия непрерывного источника сообщений
Гауссовский источник непрерывных сообщений.
1)
Сигнал:
2) Сигнал стационарный с равномерной спектральной плотностью
мощности
в полосе частот от 0 до .
-
Отсюда
Слайд 26Теория информации
Лекция 5. Энтропия непрерывного источника сообщений
3) В соответствии с
теоремой Котельникова передаём информацию с
шагом временной дискретизации.
Эти отсчеты не
коррелированны (а так как сигнал гауссовский, то инезависимы). Некоррелированность следует из
Отсюда источник отсчетов без памяти.
4) Производительность гауссовского источника при фиксированном Δx
(этим учитываем факт использования дифференциальной энтропии)
равна:
Пропускная способность гауссовского канала связи (формула
Шеннона-Таллера).
Слайд 27Теория информации
Лекция 5. Энтропия непрерывного источника сообщений
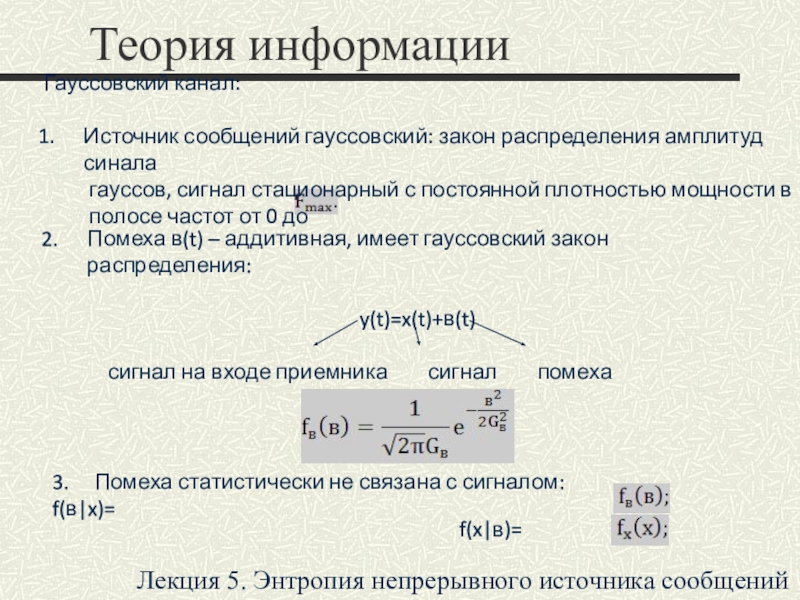
Гауссовский канал:
Источник сообщений гауссовский:
закон распределения амплитуд синала
гауссов, сигнал
стационарный с постоянной плотностью мощности в полосе частот от 0 до
Помеха в(t) – аддитивная, имеет гауссовский закон распределения:
y(t)=x(t)+в(t)
сигнал на входе приемника сигнал помеха
3. Помеха статистически не связана с сигналом: f(в|x)=
f(x|в)=
Слайд 28Теория информации
Лекция 5. Энтропия непрерывного источника сообщений
Помеха имеет постоянную спектральную
плотность мощности в
полосе канала от
0 до Отсюда следует, что отсчеты помехи с шагом временной дискретизации
статистически независимы.
Слайд 29Теория информации
Лекция 5. Энтропия непрерывного источника сообщений
Требуется определить С –
пропускную способность гауссовского канала.
При передачи отсчетов с шагом
источник
сообщений и каналОтсюда
связи «без памяти».
определяется при гауссовом источнике, дающем максимум
дифференциальной энтропии при заданной мощности, и введенной
модели аддитивной помехи.