Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ТЕОРИЯ МНОЖЕСТВ ОТНОШЕНИЯ
Содержание
- 1. ТЕОРИЯ МНОЖЕСТВ ОТНОШЕНИЯ
- 2. Цель лекции – ознакомиться и овладеть понятиями
- 3. Литература Горбатов В.А. Основы дискретной математики. М.:
- 4. ТерминыБазовые понятия: множество, подмножество, упорядоченная пара, вектор,
- 5. Def: n-местным отношением на множестве M называется
- 6. Операции над отношениями. 1Для совместимых отношений αAn, βВn имеют местоследующие операции:
- 7. Операции над отношениями. 2
- 8. Пример 1 Для совместимых тернарных отношений a,bM3a={(a,b,c), (a,b,d),
- 9. Даны множества: A={a,b}, B={a,c}Составим декартов квадрат множества
- 10. Пример 3 Даны отношения aA2, bA3a =
- 11. Отношения в совокупности с операциями образуют реляционную
- 12. Алгебра отношений. 2 Носитель реляционной алгебры представляет
- 13. Time Out Преподаватель (П) и студент (С):П:
- 14. Пример специальных операций над отношениями. Постановка задания. 1 Таблица определяет отношение реляционной модели данных:D1D2D3D4D5bg
- 15. Определить результаты выполнения следующих операций: a1 –
- 16. Пример специальных операций над отношениями. Выбор.
- 17. Def: операция выбора представляет собой процедуру
- 18. Def: операция проекции определяет построение «вертикального»
- 19. Проекция по двум и более доменам
- 20. Пример специальных операций над отношениями. Проекция. 3
- 21. Пример специальных операций над отношениями. Соединение.
- 22. Def: операция соединения по двум таблицам,
- 23. ВыводыРеляционная алгебра замкнута относительно введенных операцийОперация проецирования
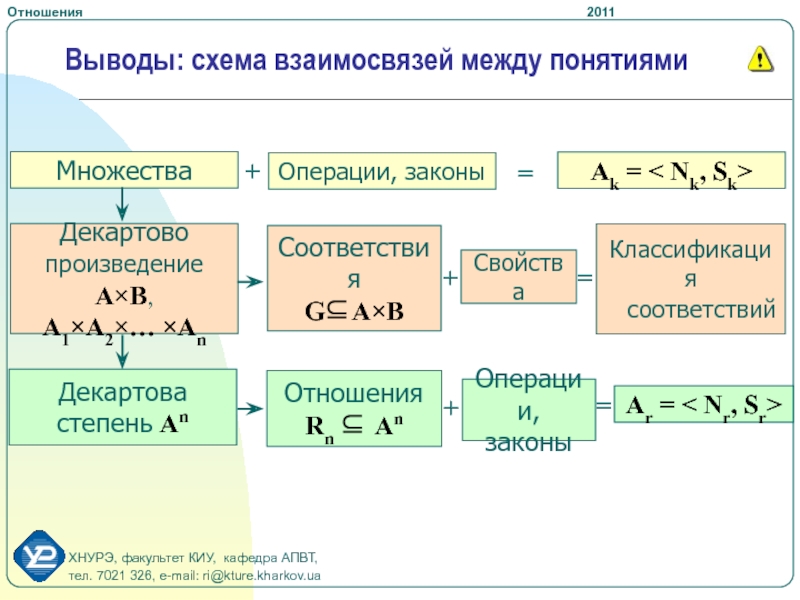
- 24. Выводы: схема взаимосвязей между понятиями
- 25. Тест-вопросы. 11. Отношением степени n называется:а) произвольное
- 26. Тест-вопросы. 24. Операция проекции представляет собой построение:а)
- 27. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1ТЕОРИЯ МНОЖЕСТВ
ОТНОШЕНИЯ
ЛЕКЦИЯ 3
Факультет компьютерной инженерии и управления, кафедра АПВТ, ХНУРЭ
Лектор
– д.т.н., проф. Хаханов В.И.
Слайд 2Цель лекции – ознакомиться и овладеть понятиями «отношение», «алгебра отношений»,
изучить операции над отношениями для применения
в задачах компьютерной инженерии
Содержание:
Понятие n-местного отношения.
Совместимость отношений
Операции над отношениями
Реляционная алгебра
Дополнительные операции над отношениями
Пример применения отношений при составлении реляционной базы данных
Тема: Отношения
Слайд 3Литература
Горбатов В.А. Основы дискретной математики. М.: Высш. шк., 1986.
9-12 с.
Лавров И.А., Максимова Л.Л. Задачи по теории множеств,
математической логике и теории алгоритмов. М.: Наука. Главная редакция физико-математической литературы, 1984. 8-12 с.Кузнецов О.П., Адельсон-Вельский Г.М. Дискретная математика для инженера. М.: Энергия, 1980. 12-21 с.
Богомолов А.М., Сперанский Д.В. Аналитические методы в задачах контроля и анализа дискретных устройств. Саратов: Изд-во Саратовского ун-та, 1986. 240с.
Новиков Ф.А. Дискретная математика для программистов. С.-П., 2001. С. 4-24.
Хаханов В.І., Хаханова І.В., Кулак Е.М., Чумаченко С.В. Методичні вказівки до практичних занять з курсу “Дискретна математика”. Харків, ХНУРЕ. 2001. 21-23 с.
Слайд 4Термины
Базовые понятия:
множество,
подмножество,
упорядоченная
пара,
вектор,
декартово (прямое) произведение множеств
Ключевые слова:
отношение,
степень отношения,
совместимость
отношений, реляционная алгебра,
операции над отношениями:
объединение,
пересечение,
разность,
расширенное декартово произведение,
выбор,
проекция,
соединение
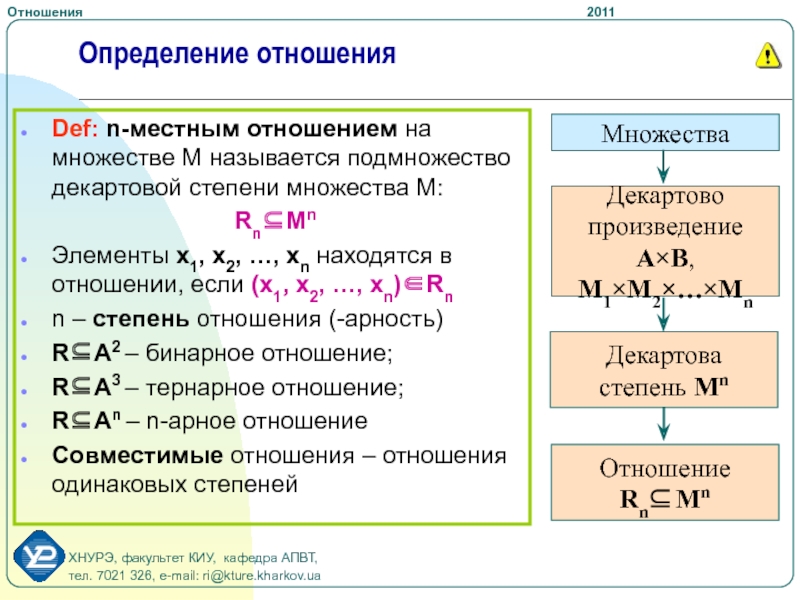
Слайд 5Def: n-местным отношением на множестве M называется подмножество декартовой степени
множества М:
RnМn
Элементы х1, х2, …, хn находятся в отношении,
если (х1, х2, …, хn)Rnn – степень отношения (-арность)
RA2 – бинарное отношение;
RA3 – тернарное отношение;
RAn – n-арное отношение
Совместимые отношения – отношения одинаковых степеней
Определение отношения
Слайд 6Операции над отношениями. 1
Для совместимых отношений αAn, βВn имеют место
следующие
операции:
Слайд 8Пример 1
Для совместимых тернарных отношений a,bM3
a={(a,b,c), (a,b,d), (b,c,e)}
b={ (a,b,d), (b,d,e),
(c,d,e)}
операции объединения, пересечения и разности определяются так:
ab ={(a,b,c), (a,b,d), (b,c,e),
(b,d,e), (c,d,e)};ab ={ (a,b,d) };
a\b ={(a,b,c), (b,c,e) }
Слайд 9Даны множества: A={a,b}, B={a,c}
Составим декартов квадрат множества В:
B2={ (a,a), (a,c),
(c,a), (c,c) }
Пусть универсальное и бинарное b отношения задаются
следующим образом: =AB={ (a,a), (a,c), (b,a), (b,c) }
b={ (a,c), (c,a) } B2
Дополнение отношения b есть:
b= \b=(AB)\b={ (a,a), (b,a), (b,c) }
Пример 2
Слайд 10Пример 3
Даны отношения aA2, bA3
a = { (a,b), (c,d),
(a,e) },
b={(a,b,c), (b,d,e)}
Расширенное декартово произведение
отношений a и b определяется
какab = { (a,b,a,b,c), (a,b,b,d,e), (c,d,a,b,c), (c,d,b,d,e), (a,e,a,b,c), (a,e,b,d,e) }
Слайд 11Отношения в совокупности с операциями образуют реляционную алгебру.
Алгебра отношений или
модель (множество с заданным отношением) широко применяются при формализации реальных
объектов, создании информационного обеспечения – разработке информационной базы данныхОсновой построения реляционной базы данных является двумерная таблица, каждый столбец которой соответствует домену (или атрибуту, являющемуся частью домена), строка – кортежу значений атрибутов, находящихся в отношении R
Алгебра отношений. 1
Слайд 12Алгебра отношений. 2
Носитель реляционной алгебры представляет собой множество отношений
Сигнатура, кроме введенных операций, включает специальные операции над отношениями:
выбор,
проекцию,
соединение
В соответствии с потребностями практики вводятся и другие операции:
обмен позициями;
удвоение позиций;
свертка, композиция.
Слайд 13Time Out
Преподаватель (П) и студент (С):
П: Знаешь?
С: Знаю!
П: Что
знаешь?
С: Предмет знаю.
П: Какой предмет?
С: Который сдаю.
П: А какой сдаешь?
С:
Ну, это Вы придираетесь. Ваш, конечно!
Слайд 14Пример специальных операций
над отношениями. Постановка задания. 1
Таблица определяет
отношение реляционной модели данных:
D1
D2
D3
D4
D5
b
g
Слайд 15Определить результаты выполнения следующих операций:
a1 – выбор по домену
D3 по значению атрибута c2 ;
a2 – проекция по домену
D5 ;a3 – проекция по доменам D2, D5 ;
a4 – соединение по домену D1 по условию «равно» для двух таблиц b (первые четыре кортежа R5) и g (вторые четыре кортежа R5).
Пример специальных операций
над отношениями. Постановка задания. 2
Слайд 16Пример специальных операций
над отношениями. Выбор. 1
a1 – выбор
по домену D3 по значению c2 :
D1
D2
D3
D4
D5
b
g
Слайд 17 Def: операция выбора представляет собой процедуру построения «горизонтального» подмножества
отношения, т.е. подмножества кортежей, обладающих заданным свойством
Пример специальных операций
над
отношениями. Выбор. 2Слайд 18 Def: операция проекции определяет построение «вертикального» подмножества отношения или
множества кортежей, получаемого выбором одних и исключением других доменов
Проекция
по одному домену определяет совокупность элементов и не является отношением:a2 – проекция по домену D5:
a2={g1,g2}
Пример специальных операций
над отношениями. Проекция. 1
D1
D2
D3
D4
D5
b
g
Слайд 19 Проекция по двум и более доменам является отношением степени
2 и более в зависимости от количества столбцов, по которым
ведется проецирование:a3 – проекция по доменам D2, D5:
Пример специальных операций
над отношениями. Проекция. 2
D1
D2
D3
D4
D5
b
g
Слайд 20Пример специальных операций над отношениями. Проекция. 3
Def: проекцией Pr(R2/A)
универсального бинарного отношения R2AB на множество А называется совокупность элементов
Pr(R2/A)={ai | (ai,bi)R2}
Def: проекцией Pr(Rn/Ai1,Ai2,…,Aim) универсального n-арного отношения Rn Ai1Ai2…Ain на множества Ai1,Ai2,…,Aim называется совокупность кортежей (ai1,ai2,…,aim), где aijAij, каждый из которых является частью n-арного вектора из отношения Rn:
Pr(Rn/Ai1,Ai2,…,Aim)={(ai1,ai2,…,aim)| aij Aij , j=1,2,…,m}
Слайд 21Пример специальных операций
над отношениями. Соединение. 1
a4 – соединение
по домену D1 по условию «равно» для двух таблиц b
(первые четыре кортежа R5) и g (вторые четыре кортежа R5):Слайд 22 Def: операция соединения по двум таблицам, имеющим общий домен,
позволяет построить одну таблицу, каждая строка которой образуется соединением двух
строк исходных таблиц. Из заданных таблиц выбираются строки, содержащие одно и то же значение из общего домена; общему домену сопоставляется один столбецПример специальных операций над отношениями. Соединение. 2
Слайд 23Выводы
Реляционная алгебра замкнута относительно введенных операций
Операция проецирования на один домен
выводит из носителя, т.е. результат выполнения операции проецирования по одному
домену отношением не являетсяПроекция на два и более домена является отношением степени два и более, соответственно
Запрос в реляционной базе данных будет выполнен тем быстрее, чем меньше операций над отношениями он содержит
Слайд 25Тест-вопросы. 1
1. Отношением степени n называется:
а) произвольное подмножество
данного множества;
б)
подмножество декартова произведения двух множеств;
в) подмножество декартова произведения любого конечного
количества
множеств;г) подмножество декартовой степени множества;
д) результат объединения данных множеств;
е) результат пересечения данных множеств.
2. Отношения являются совместимыми:
а) всегда;
б) если они имеют разные степени;
в) если они имеют одинаковые степени;
г) если они бинарные.
3. Операция выбора представляет собой построение:
а) «горизонтального» подмножества отношения;
б) «вертикального» подмножества отношения;
в) «диагонального» подмножества отношения;
г) «бинарного» подмножества отношения;
Слайд 26Тест-вопросы. 2
4. Операция проекции представляет собой построение:
а) «горизонтального»
б) «вертикального»
в) «диагонального»
подмножества отношения.
5. Операция проекции по двум доменам представляет
собой построение:а) «горизонтального» подмножества отношения;
б) «вертикального» подмножества отношения;
в) «диагонального» подмножества отношения;
г) бинарного подмножества отношения.
6. Операция проекции по одному домену представляет собой построение:
а) «горизонтального» подмножества отношения;
б) «вертикального» подмножества отношения;
в) «диагонального» подмножества отношения;
г) бинарного подмножества отношения;
д) некоторого отношения степени n;
е) множества элементов, не являющегося отношением.