Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теория вероятностей
Содержание
- 1. Теория вероятностей
- 2. Лекция № 1Основные понятия и определения теории вероятностей
- 3. Испытания, событияИспытанием (опытом, экспериментом), называется процедура, включающая
- 4. Случайность означает, что результаты такого явления могут
- 5. Классификация событийДостоверное событие - это событие, которое
- 6. Алгебра событийРазличные события и действия над ними
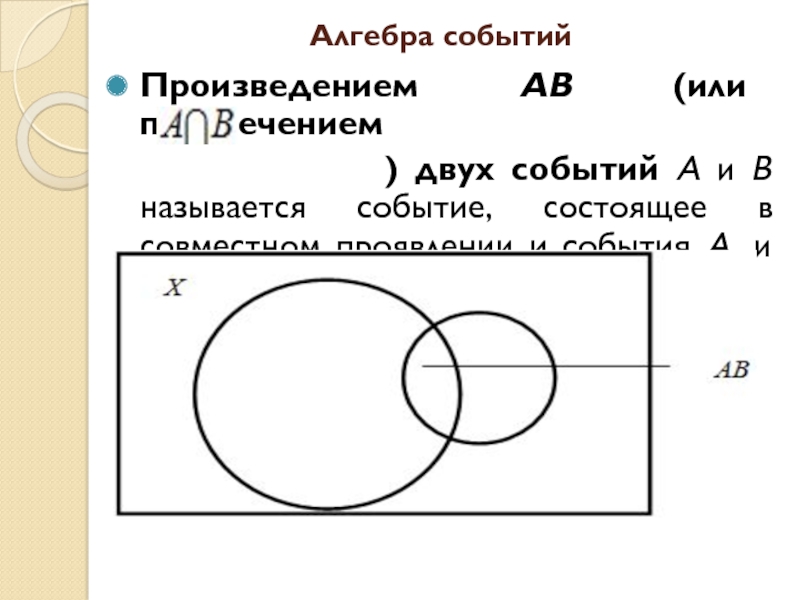
- 7. Алгебра событийПроизведением АВ (или пересечением
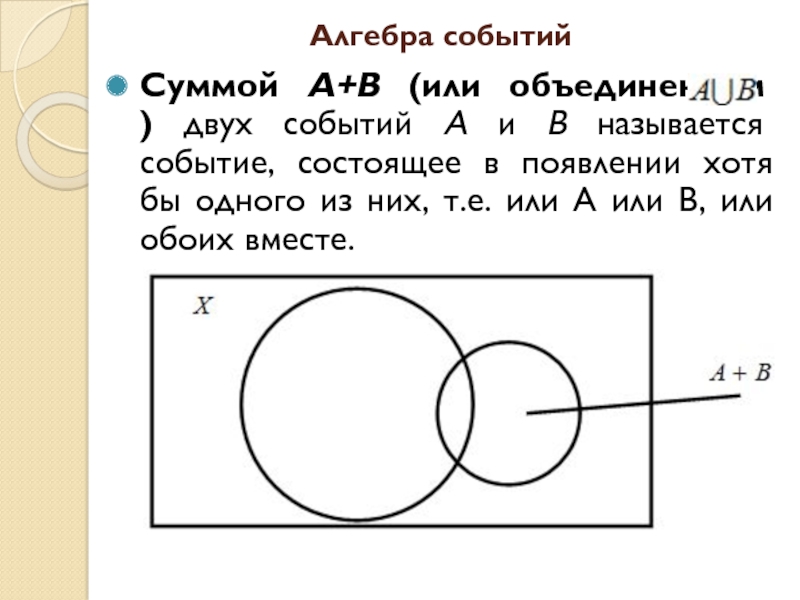
- 8. Алгебра событийСуммой А+В (или объединением
- 9. Скачать презентанцию
Лекция № 1Основные понятия и определения теории вероятностей
Слайды и текст этой презентации
Слайд 1Теория вероятностей
Кракашова Ольга Анатольевна
доцент, канд. экон. наук,
доцент кафедры
«Математическая статистика, эконометрика и актуарные расчеты» РГЭУ (РИНХ)
Слайд 3Испытания, события
Испытанием (опытом, экспериментом), называется процедура, включающая определенные условия и
удовлетворяющая двум требованиям:
1) процедура может быть повторена достаточно большое число
раз (не ограниченное) без изменения условий;2) результаты этой процедуры при ее повторении могут меняться и их нельзя однозначно предсказать.
Результатом (исходом) испытания (опыта) может быть результат наблюдения или измерения.
Теория вероятностей – это наука, которая применяется к реальным явлениям, обладающим двумя свойствами – случайностью и массовостью.
Слайд 4Случайность означает, что результаты такого явления могут быть разными и
их нельзя однозначно предсказать.
Массовость означает, что это явление не
уникальное, оно может повторяться достаточно много раз без изменения условий. Прогноз, который позволяет делать теория вероятностей, выглядит так: его результат будет появляться примерно в случаев.
Случайными событиями, или просто событиями, называются всевозможные результаты испытания.
Случайное событие может состоять из нескольких простых, элементарных событий.
Единичный, отдельный исход испытания называется элементарным событием или шансом. Например, извлечение любой карты из колоды – элементарное событие. Обозначаются события большими латинскими буквами , когда их много, пользуются индексами:
Слайд 5Классификация событий
Достоверное событие - это событие, которое обязательно произойдет в
результате испытания. Достоверные события условимся обозначать символом Ω.
Невозможное событие -
это событие, которое не может произойти в результате данного опыта (испытания). Невозможное событие обозначим .Достоверные и невозможные события, вообще говоря, не являются случайными.
Совместные события. Несколько событий называются совместными, если в результате эксперимента наступление одного из них не исключает появления других.
Несовместные события. Несколько событий называются несовместными в данном опыте, если появление одного из них исключает появления других. Например, выигрыш, ничейный исход и проигрыш при игре в шахматы (одной партии) - три несовместных события.
Единственно возможные события. События называются единственно возможными, если в результате испытания хотя бы одно из них обязательно произойдет (или одно, или два, или ... или все события из рассматриваемой совокупности событий произойдут; одно точно произойдет).
Равновозможные события. Несколько событий называются равновозможными, если в результате испытания ни одно из них не имеет объективно большую возможность появления, чем другие.
Противоположные события. Два события называются противоположными, если появление одного из них равносильно непоявлению другого. Обозначаются такие события: А и Ā.
Полная группа событий. Совокупность всех единственно возможных и несовместных событий называется полной группой событий.
Слайд 6Алгебра событий
Различные события и действия над ними удобно рассматривать с
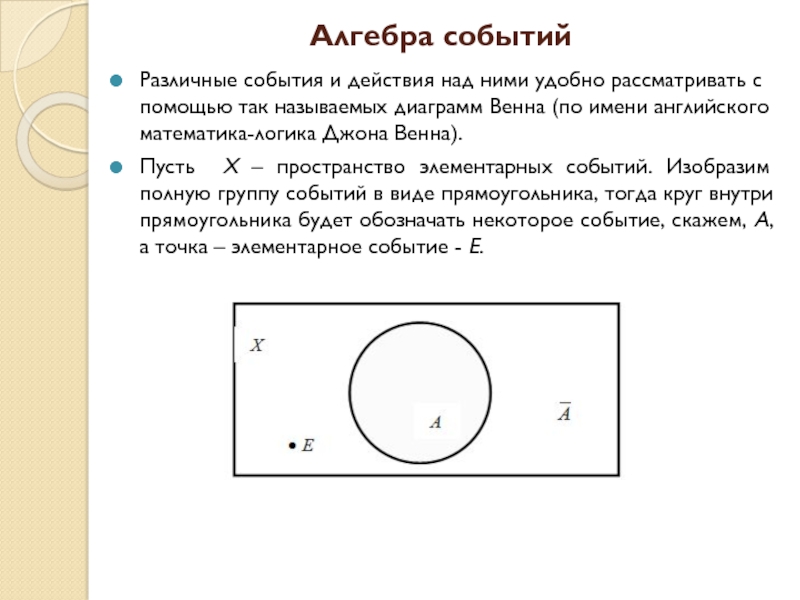
помощью так называемых диаграмм Венна (по имени английского математика-логика Джона
Венна).Пусть Х – пространство элементарных событий. Изобразим полную группу событий в виде прямоугольника, тогда круг внутри прямоугольника будет обозначать некоторое событие, скажем, А, а точка – элементарное событие - Е.