Банки и биржи, ЮНИТИ, 2001 .
Гмурман В.Е. Теория вероятностей
и математическая статистика. - М.: В.Ш., 2002 .Тимошина И.Р. Электронный конспект лекций по теории вероятностей. ВФ СПбГУСЭ, 2007.
http://www.math.spbu.ru/ru/Archive/Courses/jvr/DA_html/_lec_1_06.html
© И.Р.Тимошина «Теория вероятностей»
















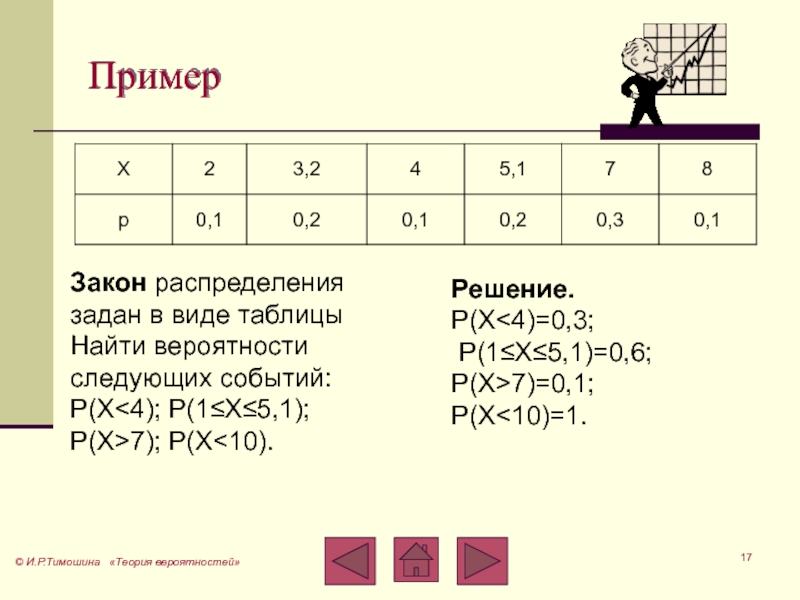


![Теория вероятностей Свойства функции распределенияЗначения функции распределения принадлежат отрезку [0, 1] или 0≤F(x) Свойства функции распределенияЗначения функции распределения принадлежат отрезку [0, 1] или 0≤F(x) ≤1Функция F(x) является неубывающей для всех](/img/thumbs/e994970526596aa8f1d21d506a59cc5e-800x.jpg)
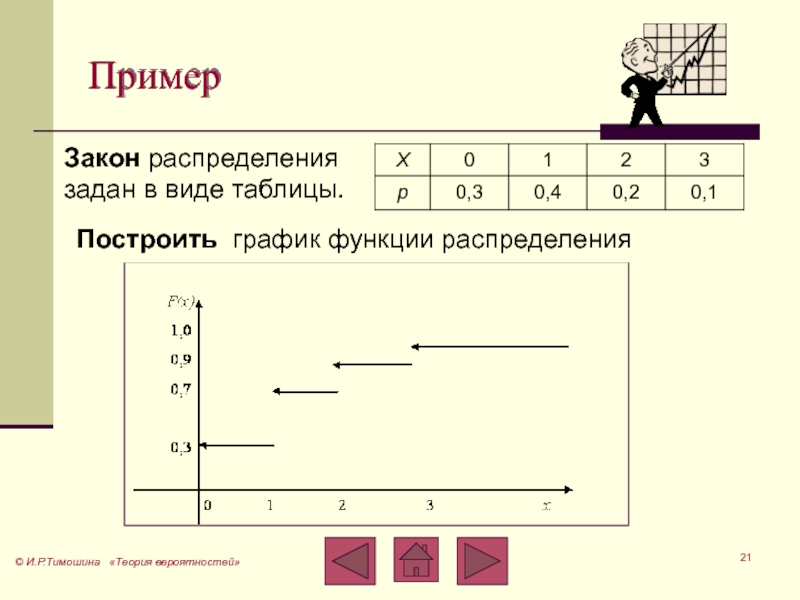
![Теория вероятностей График функции распределенияВывод. Функция распределения дискретной случайной величины является неубывающей; кусочно-постоянной; График функции распределенияВывод. Функция распределения дискретной случайной величины является неубывающей; кусочно-постоянной; область значений [0; 1]. ©](/img/thumbs/6f2781a4d24727adbe2f3f0d97557cfe-800x.jpg)