Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
Содержание
- 1. ТЕОРИЯ ВЕРОЯТНОСТЕЙ
- 2. Оригинальная подвижная викторина: Оцените возможность наступления событий,
- 3. Событие, которое происходит всегда, называют достоверным.
- 4. Два события, которые в данных условиях могут
- 5. Классическое определение вероятности. Вероятностью P события А
- 6. Алгоритм нахождения вероятности случайного события Для нахождения
- 7. Из карточек составили
- 8. Сложение и умножение вероятностей В решениях задач
- 9. Типы задач на ОГЭ1. Простые задачи на
- 10. На 100 электрических лампочек в среднем приходится
- 11. В чемпионате по гимнастике участвуют 50 спортсменок:
- 12. В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орел не выпадет ни разу.
- 13. Сколько нечетных двузначных чисел можно составить из
- 14. Известно, что в некотором регионе вероятность того,
- 15. Бросаем монеткуВытягиваем экзаменационный билетБросаем кубик2246Выпал «орел»Вытянули билет №5На кубике выпало четное число113
- 16. Вероятность того, что новый сканер прослужит больше
- 17. Биатлонист пять раз стреляет по мишеням. Вероятность
- 18. В магазине стоят два платёжных автомата. Каждый
- 19. ТЕСТВыбери классическое определение вероятности события: Вероятность
- 20. 2. Из кармана на пол выпала монета.
- 21. 3. Посеяли 100 семян. Из них взошли
- 22. 4. В коробке находятся 500 деталей, из
- 23. 5. В магазине на складе находятся 100
- 24. Ответы
- 25. Приложение 2Домашнее заданиеНа экзамене 25 билетов, Сергей
- 26. Удачи на ОГЭ!
- 27. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Оригинальная подвижная викторина:
Оцените возможность наступления событий, используя для этого
Слайд 3Событие, которое происходит всегда, называют достоверным. Событие, которое не может произойти,
называется невозможным.
Пусть из урны, содержащей
только черные шары, вынимают шар.
Тогда
появление черного шара – достоверное событие;
Появление белого
шара – невозможное событие.
Слайд 4Два события, которые в данных условиях могут происходить одновременно, называются
совместными, а те, которые не могут происходить одновременно, - несовместными.
Брошена монета. Появление «герба» исключает появление надписи. События «появился герб» и «появилась надпись» - несовместные.
Слайд 5Классическое определение вероятности.
Вероятностью P события А при проведении некоторого испытания
называют отношение числа тех исходов, в результате которых наступает событие
А (m – число благоприятных исходов), к общему числу всех (равновозможных между собой) исходов этого испытания (n – число всех возможных исходов).Слайд 6Алгоритм нахождения вероятности случайного события
Для нахождения вероятности случайного события
А при проведении некоторого испытания следует проведении некоторого испытания следует
найти:1) число N всех возможных исходов данного испытания;
Алгоритм для решения задач с помощью классического определения.
1)обозначить событие (А)
2)сосчитать число всех исходов (n)
3)сосчитать число исходов благоприятствующих данному событию (m)
4)найти отношение благоприятствующих исходов к числу всех исходов
Слайд 7
Из карточек составили слово «пирамида». Какую
карточку с буквой вероятнее всего вытащить? Какие события равновероятные?
Всего 8
букв.Буква «и» встречается 2 раза – P = 2/8= 1/4;
буква «а» встречается 2 раза – P= 2/8= 1/4;
остальные 1 раз– P = 1/8.
Карточку с какой буквой вероятнее всего вытащить?
Какие события равновероятные?
Слайд 8Сложение и умножение вероятностей
В решениях задач этого блока используются следующие
утверждения из теории вероятности.
Вероятность Р(С) наступления хотя бы одного из
двух несовместных событий А и В равна сумме их вероятностей.Р(С) = Р(А + В) = Р(А) + Р(В)
Вероятность противоположного события : Р(А) = 1 - Р(А).
Вероятность Р(С) совместного наступления двух независимых событий А и В равна произведению вероятностей событий А и В.
Р(С) = Р(А) Р(В)
Слайд 9Типы задач на ОГЭ
1. Простые задачи на классическое определение вероятности
А)Задачи
на брак, неисправность, выученный и невыученный билет, наличие приза
Б) Задачи
на чашки различных цветов, такси различных цветов, подарки (пазлы, машинки, книжки), пирожки разных начинок, начало игры девочкой, мальчикомВ) Задачи на команды из разных стран и на первоначальное владение мячом
2. Задачи с монетами, игральными кубиками, карточками (задачи, в которых используется метод перебора возможных вариантов)
3. Частота рождения девочек, мальчиков.
4. Сложение и умножение вероятностей (стрелок стреляет по мишени, на работу принтера, сканера, кофемашины какое-то количество лет
Слайд 10На 100 электрических лампочек в среднем приходится 25 бракованных. Какова
вероятность купить исправную лампочку?
Опыт имеет 100 равновозможных
исходов, т.е. п
= 100.Число благоприятных исходов
т = 100 – 25 = 75.
Вероятность того, что лампочка
будет исправной
Слайд 11В чемпионате по гимнастике участвуют 50 спортсменок: 17 из России,
22 из США, остальные — из Китая. Порядок, в котором
выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Китая.Решение
Число вариантов выбора спортсменки, выступающей первой, из разных стран: n = 50.
Число вариантов выбора спортсменки, выступающей первой, из Китая: m = 50 - (17 + 22) = 11.
Искомая вероятность:
Ответ: 0,22.
Слайд 12В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того,
что орел не выпадет ни разу.
Слайд 13Сколько нечетных двузначных чисел можно составить из цифр 1, 3,
4, 6, 7, 8, 9?
Решение
Составим таблицу: слева первый столбец
- первые цифры искомых чисел, вверху первая строка - вторые цифры.Ответ: 28.
Слайд 14Известно, что в некотором регионе вероятность того, что родившийся младенец
окажется мальчиком, равна 0,512. В 2010 г. в этом регионе
на 1000 родившихся младенцев в среднем пришлось 477 девочек. Насколько частота рождения девочек в 2010 г. в этом регионе отличается от вероятности этого события?Решение.
Частота cобытия «рождение девочки» равна 477 : 1000 = 0,477. Вероятность рождения девочки в этом регионе равна 1 − 0,512 = 0,488. Поэтому частота данного события отличается от его вероятности на 0,488 − 0,477 = 0,011.
Ответ: 0,011.
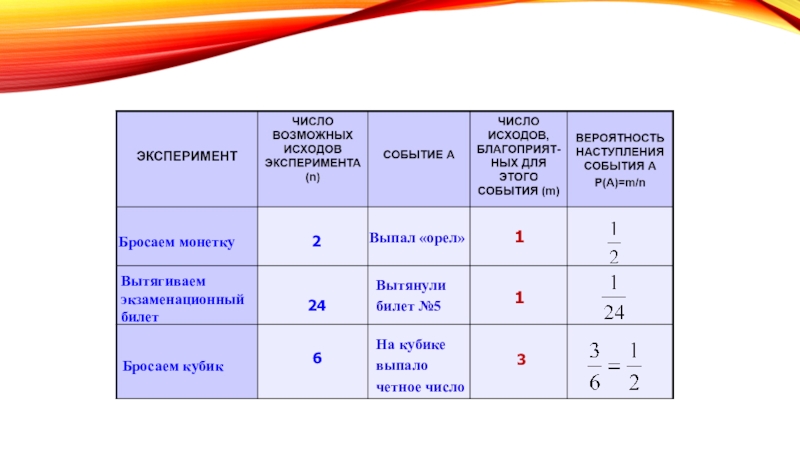
Слайд 15Бросаем монетку
Вытягиваем экзаменационный билет
Бросаем кубик
2
24
6
Выпал «орел»
Вытянули
билет №5
На кубике
выпало
четное число
1
1
3
Слайд 16Вероятность того, что новый сканер прослужит больше года, равна 0,94.
Вероятность того, что он прослужит больше двух лет, равна 0,87.
Найдите вероятность того, что он прослужит меньше двух лет, но больше года.Решение.
Пусть A = «сканер прослужит больше года, но меньше двух лет», В = «сканер прослужит больше двух лет», С = «сканер прослужит ровно два года», тогда A + B + С = «сканер прослужит больше года».
События A, В и С несовместные, вероятность их суммы равна сумме вероятностей этих событий. Вероятность события С, состоящего в том, что сканер выйдет из строя ровно через два года — строго в тот же день, час и секунду — равна нулю. Тогда:
P(A + B + С) = P(A) + P(B) + P(С)= P(A) + P(B),
откуда, используя данные из условия, получаем
0,94 = P(A) + 0,87.
Тем самым, для искомой вероятности имеем:
P(A) = 0,94 − 0,87 = 0,07.
Ответ: 0,07.
Слайд 17Биатлонист пять раз стреляет по мишеням. Вероятность попадания в мишень
при одном выстреле равна 0,7. Найдите вероятность того, что биатлонист
первые четыре раза попал в мишени, а последний раз промахнулся. Результат округлите до сотых.Решение
Вероятность попадания в мишень равна 0,7;
вероятность промаха равна 1 – 0,7 = 0,3.
Т. к. результаты выстрелов – независимые события, вероятность того, что биатлонист четыре раза попал в мишень, а один раз промахнулся, равна:
Р= 0,7 ∙ 0,7 ∙ 0,7 ∙ 0,7 ∙ 0,3 ≈ 0,07
Ответ: 0,07
Слайд 18В магазине стоят два платёжных автомата. Каждый из них может
быть неисправен с вероятностью 0,07 независимо от другого автомата. Найдите
вероятность того, что хотя бы один автомат исправен.Решение.
Найдем вероятность того, что неисправны оба автомата.
Эти события независимые, значит вероятность будет равна произведению вероятностей этих событий: 0,07∙0,07 = 0,0049.
Значит, вероятность того, что исправны оба автомата или какой-то из них будет равна 1 – 0,0049 = 0,9951.
Слайд 19ТЕСТ
Выбери классическое определение вероятности события:
Вероятность события -
1. это отношение
числа благоприятных для события исходов испытания к числу всех равновероятных
исходов.2. это отношение числа неблагоприятных для события исходов испытания к числу всех равновероятных исходов.
3. это отношение числа всех исходов испытания к числу благоприятных для события исходов.
4. это отношение числа всех исходов испытания к числу неблагоприятных для события исходов
Слайд 202. Из кармана на пол выпала монета. Найти вероятность того,
что выпал "орел":
2
0,5
1
0,2
0,1
Слайд 213. Посеяли 100 семян. Из них взошли 85%. Событие А
= {взошло семечко}. Чему равна вероятность события А?
0,85
85
100/85
185
Слайд 224. В коробке находятся 500 деталей, из которых 7 -
бракованные. Событие В = {наугад из коробки достали бракованную деталь} Чему
равна вероятность события В?500/7
7/500
3500
350
Слайд 235. В магазине на складе находятся 100 лампочек. Из них
10 - не кондиция. Событие С = {наугад достали хорошую лампочку}. Найти
вероятность события С: 0,190
9
0,9
Слайд 25Приложение 2
Домашнее задание
На экзамене 25 билетов, Сергей не выучил 3
из них. Найдите вероятность того, что ему попадётся выученный билет.
Коля
выбирает трехзначное число. Найдите вероятность того, что оно делится на 5.Телевизор у Маши сломался и показывает только один случайный канал. Маша включает телевизор. В это время по трем каналам из двадцати показывают кинокомедии. Найдите вероятность того, что Маша попадет на канал, где комедия не идет.
На тарелке 12 пирожков: 5 с мясом, 4 с капустой и 3 с вишней. Наташа наугад выбирает один пирожок. Найдите вероятность того, что он окажется с вишней.
В каждой десятой банке кофе согласно условиям акции есть приз. Призы распределены по банкам случайно. Варя покупает банку кофе в надежде выиграть приз. Найдите вероятность того, что Варя не найдет приз в своей банке.
В чемпионате по футболу участвуют 16 команд, которые жеребьевкой распределяются на 4 группы: A, B, C и D. Какова вероятность того, что команда России не попадает в группу A?
Определите вероятность того, что при бросании кубика выпало число очков, не большее 3.
Стрелок 4 раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,5. Найдите вероятность того, что стрелок первые 3 раза попал в мишени, а последний раз промахнулся.
Известно, что в некотором регионе вероятность того, что родившийся младенец окажется мальчиком, равна 0,486. В 2011 г. в этом регионе на 1000 родившихся младенцев в среднем пришлось 522 девочки. Насколько частота рождения девочки в 2011 г. в этом регионе отличается от вероятности этого события?
В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадет ровно 1 раз.










































![[ Личный бренд как один из способов продвижения чтения: презентация проекта ]](/img/thumbs/e99feefa36c4c4df7a776e5ba3c5f4f5-800x.jpg)