Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теория вероятностей и математическая статистика физический факультет 2018-2019
Содержание
- 1. Теория вероятностей и математическая статистика физический факультет 2018-2019
- 2. Слайд 2
- 3. Образовательный портал ИГУ Запись на курс Теория вероятностей и математическая статистика
- 4. Теория вероятностей и математическая статистика1. Элементы комбинаторики2.
- 5. Случайные события и величиныЗащита решения любых 5
- 6. зачет БРС 60 + 30
- 7. Слайд 7
- 8. Домашняя исследовательская работаЦентральная предельная теорема и ее
- 9. http://eek.diary.ru/p47642323.htmhttp://www.matburo.ru/st_subject.php?p=tvТеория вероятностей: учебники, лекции, сайтыOn-line ресурсы по теории вероятностей
- 10. Т.Л. Агекян Теория вероятностей для астрономов и
- 11. Пытьев Ю. П. Шишмарев И. А. Курс
- 12. Гнеденко Б.В. Курс теории вероятностей: Учебник. -
- 13. Гмурман В. Е. Теория вероятностей и математическая
- 14. Вуколов Э. Л. Основы статистического анализа. Практикум
- 15. Свешников А.А. Сборник задач по теории вероятностей,
- 16. Кремер Н.Ш. Теория вероятностей и математическая статистика:
- 17. В. А. Ватутин и др. Теория вероятностей
- 18. планированиелекции5.09 – Случайные события19.093.1017.1031.1014.11 – Многомерные случайные
- 19. Теория вероятностей – математическая наука, Изучающая закономерности
- 20. Связь схем выбора и размещения
- 21. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Теория вероятностей
и
математическая статистика
физический факультет
2018-2019 уч.год
Тюрнева Т.Г., доцент
Кафедра теории
вероятностей и дискретной математики ИМЭИ ИГУ
Слайд 4Теория вероятностей и математическая статистика
1. Элементы комбинаторики
2. Случайные события
3. Случайные
величины
Одномерные с.в.
Многомерные с.в.
4. Предельные теоремы т.в.
5. Элементы математической статистики
25 задач
+защита решения
Контрольная работа
Семестровое задание
Домашняя исследовательская работа
Домашняя контрольная работа
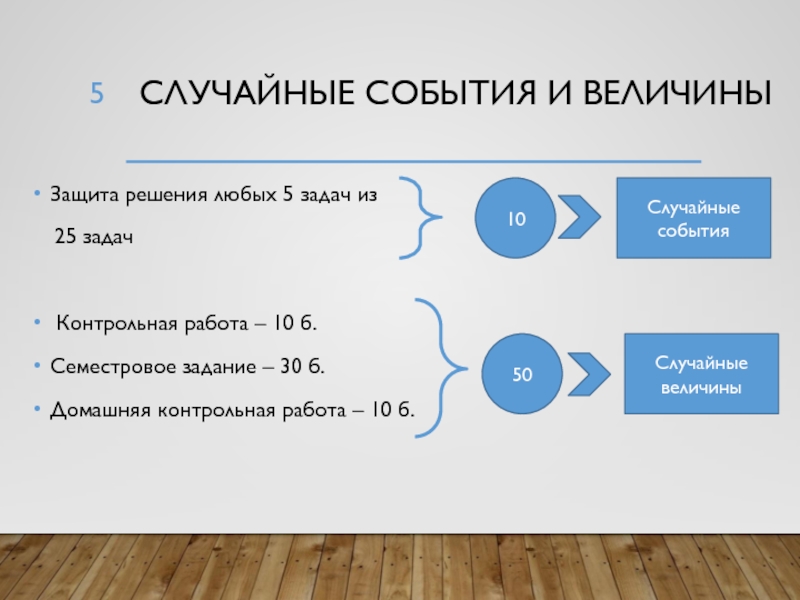
Слайд 5Случайные события и величины
Защита решения любых 5 задач из
25 задач
Контрольная работа – 10 б.
Семестровое задание –
30 б. Домашняя контрольная работа – 10 б.
10
50
Случайные события
Случайные величины
Слайд 8Домашняя исследовательская работа
Центральная предельная теорема и ее следствия.
Проверить выполнение
ЦПТ.
4.1. Сгенерировать результаты наблюдений случайных величин
Хi ~ R (0,1),
i=1, 2, ….n. !!!!4.2. Образовать суммы: S2=X1+X2, S3= X1+X2 +X3 , …. Sn= X1+X2+…Xn.
4.3. Построить гистограммы для X1, S2, S3, …. Sn.
Слайд 9http://eek.diary.ru/p47642323.htm
http://www.matburo.ru/st_subject.php?p=tv
Теория вероятностей: учебники, лекции, сайты
On-line ресурсы по теории вероятностей
Слайд 10Т.Л. Агекян Теория вероятностей для астрономов и физиков. М., Главная
редакция физико-математической литературы издательства «Наука», 1974. - 264 стр. В книге
изложены элементы теории вероятностей в том виде, в каком они должны в первую очередь находить применение в астрономии и физике. Предназначение книги требовало удобства использования излагаемого материала для исследований в области астрономии и физики. Приведено значительное число примеров, главным образом астрономических и физических. Книга может быть использована в качестве учебного пособия при чтении курса теории вероятностей для студентов университетов, специализирующихся по астрономии и физике.Слайд 11Пытьев Ю. П. Шишмарев И. А. Курс теории вероятностей и
математической статистики для физиков: Учеб. пособие. — М.: Изд-во Моск.
ун-та, 1983. — 256 с.В основу книги положен полугодовой курс лекций, читаемый авторами на физическом факультете. Большое место уделено теории случайных процессов: марковских и стационарных. Изложение математически строгое, хотя и не основанное на использовании интеграла Лебега. Часть курса, посвященная математической статистике, содержит разделы, ориентированные на приложения к задачам автоматизации планировании, анализа и интерпретации физических экспериментов. Включены элементы теории статистической проверки гипотез, используемые в задаче интерпретации экспериментальных данных.
Слайд 12Гнеденко Б.В. Курс теории вероятностей: Учебник. - Изд. 8-е, испр.
и доп. — М.: Едиториал УРСС, 2005. — 448 с.
(Классический университетский учебник.). Дается систематическое изложение основ теории вероятностей, проиллюстрированное большим числом подробно рассмотренных примеров, в том числе и прикладного содержания. Серьезное внимание уделено рассмотрению вопросов методологического характера.Слайд 13Гмурман В. Е. Теория вероятностей и математическая статистика - М.,
Высш.шк., 2003.- 479 с. Учебное пособие содержит в основном весь материал
программы по теории вероятностей и математической статистике. Большое внимание уделено статистическим методам обработки экспериментальных данных. В конце каждой главы помещены задачи с ответами. Предназначается для студентов вузов и лиц, использующих вероятностные и статистические методы при решении практических задач.Гмурман В. Е. Руководство к решению задач по теории вероятностей и математической статистике. - М., Высш.шк., 2004.- 404 с. В руководстве к решению задач приведены необходимые теоретические сведения и формулы, даны решения типовых задач, помещены задачи для самостоятельного решения, сопровождающиеся ответами и указаниями. Большое внимание уделено методам статистической обработки экспериментальных данных.
Слайд 14Вуколов Э. Л. Основы статистического анализа. Практикум по статистическим методам
и исследованию операции с использованием пакетов STATISTICA и EXCEL: учебное
пособие. — 2-е изд., исправ. и доп.. — М.: ФОРУМ. 2008. — 464 с. — (Высшее образование). Книга является учебно-методическим пособием по теории вероятностей, статистическим методам и исследованию операций. Приведены необходимые теоретические сведения и подробно рассматривается решение задач прикладной статистики с использованием пакета STATISTICA. Излагаются основы симплекс-метода и рассматривается решение задач исследования операций средствами пакета EXCEL. Приводятся варианты заданий и методические разработки по основным разделам статистики и исследования операций.Слайд 15Свешников А.А. Сборник задач по теории вероятностей, математической статистике и
теории случайных величин - Изд.: Лань, 2008, 448 стр. . Дается систематическое
изложение основ теории вероятностей, проиллюстрированное большим числом подробно рассмотренных примеров, в том числе и прикладного содержания. Серьезное внимание уделено рассмотрению вопросов методологического характера.Слайд 16Кремер Н.Ш. Теория вероятностей и математическая статистика: Учебник для вузов.
— 2-е изд., перераб. и доп.— М.: ЮНИТИ-ДАНА, 2004. -
573 с. Основной принцип, которым руководствовался автор при подготовке курса теории вероятностей и математической статистики для экономистов, — повышение уровня фундаментальной математической подготовки студентов с усилением ее прикладной экономической направленности. При этом это не только учебник, но и краткое руководство к решению задач. Приводятся примеры использования вероятностных и математико-статистических методов в задачах массового обслуживания и моделях финансового рынка. Задачи для самостоятельной работы рассматриваются в конце каждой главы в рубрике «Упражнения». Необходимые для решения задач математико-статистические таблицы даются в приложении.Слайд 17В. А. Ватутин и др. Теория вероятностей и математическая статистика
в задачах: Учеб. пособие для вузов/В. А. Ватутин, Г. И.
Ивченко, Ю- И. Медведев и др. — 2-е изд., испр. — М.: Дрофа, 2003. — 328 с: ил. Для каждой модели приведены краткие теоретические сведения, примеры решения задач и задачи дли самостоятельного решения. Среди прикладных задач имеются задачи по теории страхования и экономике. Книга может быть использована для нескольких целей: 1. как справочник, позволяющий быстро найти образец решения того или иного класса задач; 2. для самостоятельного изучения теории вероятностей и математической статистики; 3. как основа ознакомительного курса теории вероятностей.Слайд 18планирование
лекции
5.09 – Случайные события
19.09
3.10
17.10
31.10
14.11 – Многомерные случайные величины
28.11 – Предельные
теоремы т.в.
12.12 – Математическая статистика
26. 12 – зачет
практика
5 (12).09 -
комбинаторика 19 (26).09 – случайные события
3 (10).10 – случайные величины
17 (24).10 – случайные величины
31(7).10 – контрольная работа
14 (21).11 – защита семестрового задания
28 (5).11 – сдать д.к.р.
12 (19).12 – ЗАЧЕТ
26.12 – ЗАЧЕТ
Одномерные случайные
величины
1
2
3
4
5
6
7
8
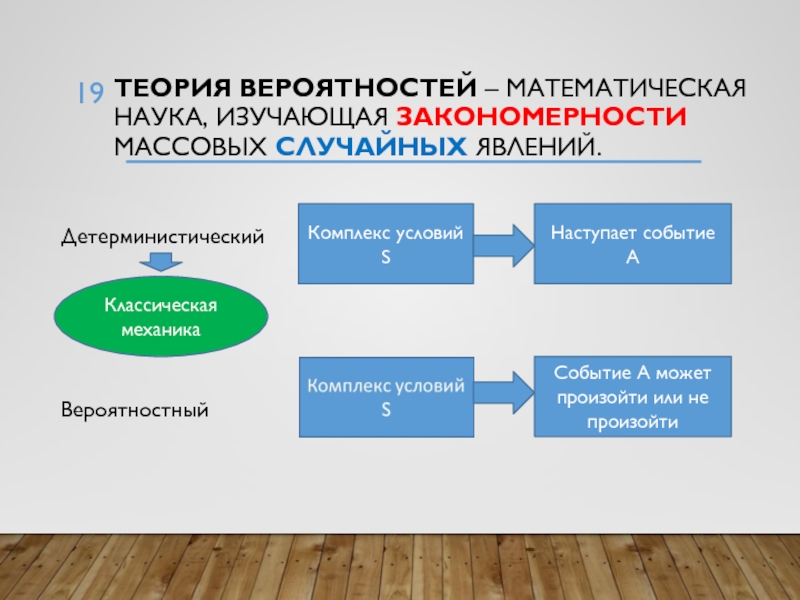
Слайд 19Теория вероятностей – математическая наука, Изучающая закономерности массовых случайных явлений.
Детерминистический
Вероятностный
Комплекс условий S
Наступает событие А
Событие А может произойти или
не произойтиКлассическая механика