Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теория вероятности и математическая статистика
Содержание
- 1. Теория вероятности и математическая статистика
- 2. ЛИТЕРАТУРА:1. Вентцель Е.С. Теория вероятностей. – М.:
- 3. ВОПРОС 1: Введение. Проблема неопределенности
- 4. "Нет ничего более противного разуму
- 5. "Случай - это ничто.
- 6. Пьер-Симон Лаплас (1749, Кальвадос — 1827,
- 7. СлучайностьФормирование решений, в том числе и научных,
- 8. Определение. Теория вероятностей — раздел математики, изучающий
- 9. ВОПРОС 2: История теории вероятностей
- 10. ЗАДАЧИ КАВАЛЕРЕ ДЕ МЕРЕПри четырехкратном бросании игральной
- 11. Якоб БернуллиЛаплас, ПуассонДе Муавр, Монмор, Н. Бернулли,
- 12. ВОПРОС 3: Случайные событияСлучайными событиями, называются события
- 13. СОБЫТИЕ. АЛГЕБРА СОБЫТИЙΩΛДостоверное событие ΩНевозможное событие ΛОбъединение
- 14. СОБЫТИЕ. АЛГЕБРА СОБЫТИЙΩΛДостоверное событие ΩНевозможное событие ΛОбъединение
- 15. Определения. Суммой событий A и B называется
- 16. Определения. Произведением событий A и B называется
- 17. Разностью событий A и B называется событие,
- 18. ВОПРОС 4: Вероятность случайного события
- 19. КЛАССИЧЕСКОЕ ОПРЕДЕЛЕНИЯ ВЕРОЯТНОСТИЯ. Бернулли
- 20. ОСНОВНЫЕ СВОЙСТВА ВЕРОЯТНОСТИ 1. 0≤P(A) ≤1;
- 21. СТАТИСТИЧЕСКОЕ ОПРЕДЕЛЕНИЯ ВЕРОЯТНОСТИ
- 22. ВОПРОС 5:Алгебра вероятностного пространства
- 23. Вероятность суммы событийЕсли события A и B несовместны, то
- 24. Определение. Условная вероятность Определение. События A и B называются независимыми, если
- 25. Определение. Вероятность произведенияВероятность произведения событийДля независимых событий
- 26. ВОПРОС 6:Формула полной вероятности
- 27. Слайд 27
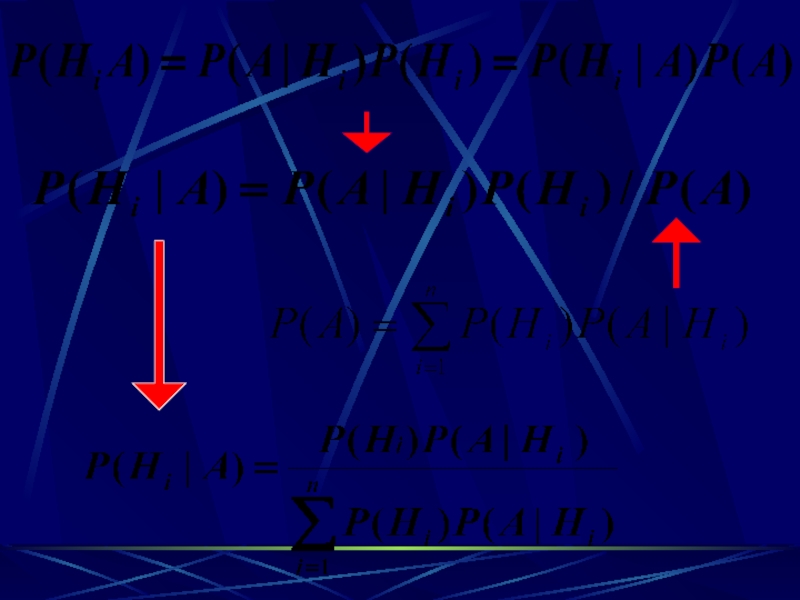
- 28. ВОПРОС 7:Формула Байеса
- 29. AP(A|Hi)=pi, i=1,…,n..P(Hi|A)=??? H1H2H3Ω
- 30. Слайд 30
- 31. Томас Байес (Reverend Thomas Bayes]) (1702 —
- 32. ВОПРОС 8:Основные формулы комбинаторики
- 33. Перестановки – это комбинации, составленные из всех
- 34. Размещения – комбинации из т элементов множества,
- 35. Сочетания – неупорядоченные наборы из т элементов
- 36. ВОПРОС 9:Последовательные испытания. Формула Бернулли
- 37. Последовательные испытания
- 38. Слайд 38
- 39. Формула Бернулли
- 40. Якоб Бернулли (1654, Базель —1705, там же) — швейцарский
- 41. Пример 1. Вероятность попадания в цель при
- 42. НАИВЕРОЯТНЕЙШЕЕ ЧИСЛО НАСТУПЛЕНИЯ СОБЫТИЯ A В ДАННОЙ СЕРИИ ОПЫТОВ
- 43. ВОПРОС 10:Приближение Лапласа для схемы Бернулли
- 44. Слайд 44
- 45. ВОПРОС 11:Приближение Пуассона для схемы Бернулли
- 46. Предположения:При большом числе испытаний вероятность появления А
- 47. Скачать презентанцию
ЛИТЕРАТУРА:1. Вентцель Е.С. Теория вероятностей. – М.: Наука, 1964.2. Е. С. Вентцель, Л. А. Овчаров. Задачи и упражнения по теории вероятностей: Учеб. пособие для студ. втузов — 5-е изд. — М.:
Слайды и текст этой презентации
Слайд 2ЛИТЕРАТУРА:
1. Вентцель Е.С. Теория вероятностей. – М.: Наука, 1964.
2. Е.
С. Вентцель, Л. А. Овчаров. Задачи и упражнения по теории
вероятностей: Учеб. пособие для студ. втузов — 5-е изд. — М.: Издательский центр «Академия», 2003. — 448 с.3. Гмурман, В. Е. Руководство к решению задач по теории вероятностей и математической статистике: Учеб. пособие — М.: Высшее образование, 2006.- 404 с.
Слайд 4"Нет ничего более противного разуму и природе,
чем случайность“ Аристотель.
ДЕТЕРМИНИЗМ
Аристотель (384
до н. э., Стагир — 322 до н. э., остров Эвбея) — древнегреческий философ. Ученик Платона. С 343 до н. э. — воспитатель Александра Македонского. В 335/4 г. до н. э. основал перипатетическую школу Ликей. Натуралист классического периода. Наиболее влиятельный из диалектиков древности; основоположник формальной логики. Создал понятийный аппарат, который до сих пор пронизывает философский лексикон и сам стиль научного мышления. Будущее предопределено и определяется жесткой схемой причинно-следственных связей
или божественным промыслом.
Слайд 5 "Случай - это ничто. Случая не существует.
Мы называем так действие, причины которого не понимаем. Нет действия
без причины, нет существования без основания существовать. Это первый принцип всех истинных философов».Вольтер (Франсуа-Мари Аруэ)
(1694-1778гг.)
ДЕТЕРМИНИЗМ
Слайд 6 Пьер-Симон Лаплас (1749, Кальвадос — 1827, Париж) — выдающийся
французский математик, физик и астроном; известен работами в области небесной
механики, дифференциальных уравнений, один из создателей теории вероятностей.«То, что мы знаем,— ограничено, а то, чего мы не знаем — бесконечно».
ДЕТЕРМИНИЗМ
Принцип детерминизма: при обладании необходимым объемом достоверной информации любое событие в будущем является абсолютно прогнозируемым.
Слайд 7Случайность
Формирование решений, в том числе и научных, осуществляется в условиях
неопределенности.
Генезис неопределенности:
недостаточность знаний об объекте исследования и среды взаимодействия
Слайд 8Определение.
Теория вероятностей — раздел математики, изучающий закономерности случайных явлений
и процессов.
Вероятность (вероятностная мера) — численная мера возможности наступления некоторого
события.
Слайд 10ЗАДАЧИ КАВАЛЕРЕ ДЕ МЕРЕ
При четырехкратном бросании игральной кости, что происходит
чаще: хотя бы один раз выпадает шестерка или шестерка не
выпадет ни разу?Как правильно разделить банк из начальных ставок при игре в кости, если игра завершается ранее числа заранее оговоренных партий
АЗАРТНЫЕ ИГРЫ
БЛЕЗ ПАСКАЛЬ, ПЬЕР ФЕРМА, ХРИСТИАН ГЮЙГЕНС
Слайд 11Якоб Бернулли
Лаплас, Пуассон
Де Муавр, Монмор, Н. Бернулли, Д. Бернулли, Л.
Эйлера, Т. Байеса, Ж. Даламбера
П. Л. Чебышев, М.В. Остроградский,
В.Я. Буняковский, А.А. Марков, А. М. ЛяпуновАндрей Николаевич Колмогоров
ТВОРЦЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
Слайд 12ВОПРОС 3:
Случайные события
Случайными событиями, называются события ω, которые могут
произойти или не произойти и образующих в совокупности пространства элементарных
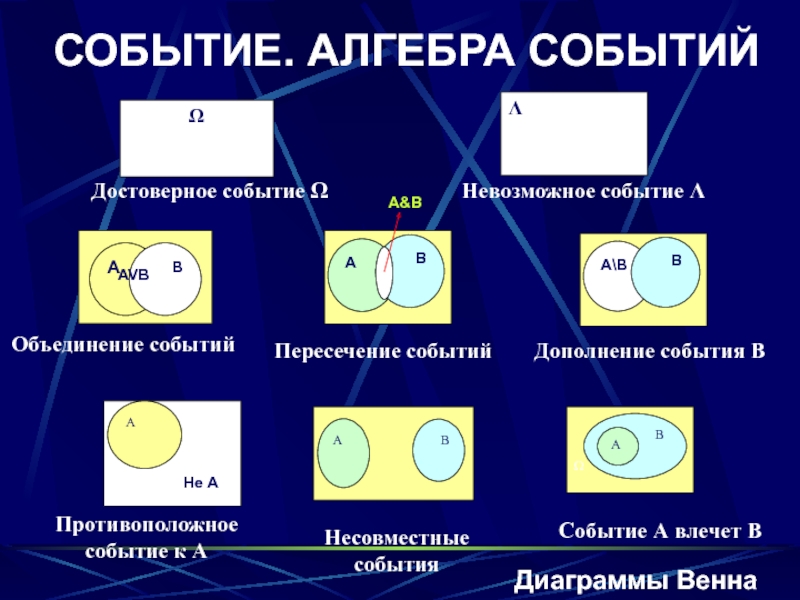
событий случайных событий Ω={ω}.
Слайд 13СОБЫТИЕ. АЛГЕБРА СОБЫТИЙ
Ω
Λ
Достоверное событие Ω
Невозможное событие Λ
Объединение событий
Пересечение событий
Дополнение события
B
Противоположное событие к А
Несовместные события
Событие А влечет B
Диаграммы
Венна
Слайд 14СОБЫТИЕ. АЛГЕБРА СОБЫТИЙ
Ω
Λ
Достоверное событие Ω
Невозможное событие Λ
Объединение событий
Пересечение событий
Дополнение события
B
Противоположное событие к А
Несовместные события
Событие А влечет B
Диаграммы
Венна
Слайд 15Определения.
Суммой событий A и B называется событие, состоящее из
всех
элементарных событий,
принадлежащих одному из событий A или B.
Обозначается A + B.
Слайд 16Определения.
Произведением событий A и B
называется событие, состоящее
из
всех элементарных событий,
принадлежащих одновременно
событиям A и B.
Обозначается
AB.
Слайд 17Разностью событий A и B называется событие, состоящее из всех
элементарных
событий принадлежащих A,
но не принадлежащих B.
Обозначается A\B.
Определения.
Слайд 20ОСНОВНЫЕ СВОЙСТВА ВЕРОЯТНОСТИ
1. 0≤P(A) ≤1;
2. P(Ω)=1;
3.
P(Λ)=0;
4. P(¬A)=1- P(A);
5. Если A и B несовместны,
то P(A∪B)=p(A)+P(B);6. В общем же случае P(A∪B)=p(A)+P(B)- P(A∩B);
7. Если A⊆B, то P(A) ≤P(B);
Слайд 25Определение. Вероятность произведения
Вероятность произведения событий
Для независимых событий
Слайд 31Томас Байес
(Reverend Thomas Bayes]) (1702 — 1761) — английский
математик и пресвитерианский священник, член Лондонского королевского общества.
Обучался дома, в
1719 году поступил в Эдинбургский университет. ![Томас Байес (Reverend Thomas Bayes]) (1702 — 1761) — английский математик и пресвитерианский священник, член Лондонского королевского](/img/thumbs/80bd537b33165f1923ae087115f36130-800x.jpg "Теория вероятности и математическая статистика Томас Байес (Reverend Thomas Bayes]) (1702 — 1761) — английский математик")
Слайд 33Перестановки – это комбинации, составленные из всех n элементов данного
множества и отличающиеся только порядком их расположения.
Рn = n!
Слайд 34Размещения – комбинации из т элементов множества, содержащего n различных
элементов, отличающиеся либо составом элементов, либо их порядком.
Слайд 35Сочетания – неупорядоченные наборы из т элементов множества, содержащего n
различных элементов (то есть наборы, отличающиеся только составом элементов).
Слайд 40Якоб Бернулли (1654, Базель —1705, там же) — швейцарский математик, профессор математики
Базельского университета (с 1687 года). Один из основателей теории вероятностей
и математического анализа. Старший брат Иоганна Бернулли. Иностранный член Парижской Академии наук (1699) и Берлинской академии наук (1701).
Слайд 41Пример 1. Вероятность попадания в цель при одном выстреле равна
0,6. Какова вероятность того, что 8 выстрелов дадут 5 попаданий?
Слайд 46
Предположения:
При большом числе испытаний вероятность появления А в одном опыте
мала;
Произведение nр = λ сохраняет постоянное значение для разных серий
опытов
