Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Типы АЦП
Содержание
- 1. Типы АЦП
- 2. АЦП параллельного преобразованияАЦП прямого преобразования получили широкое
- 3. Слайд 3
- 4. Принцип действия АЦП предельно прост: входной сигнал
- 5. АЦП последовательного приближенияАЦП последовательного приближения реализует алгоритм
- 6. Аналого-цифровой преобразователь последовательного приближения (SAR, Successive Approximation
- 7. Слайд 7
- 8. Таким образом, АЦП последовательного приближения состоит из
- 9. Достоинством устройства является относительно высокая скорость преобразования:
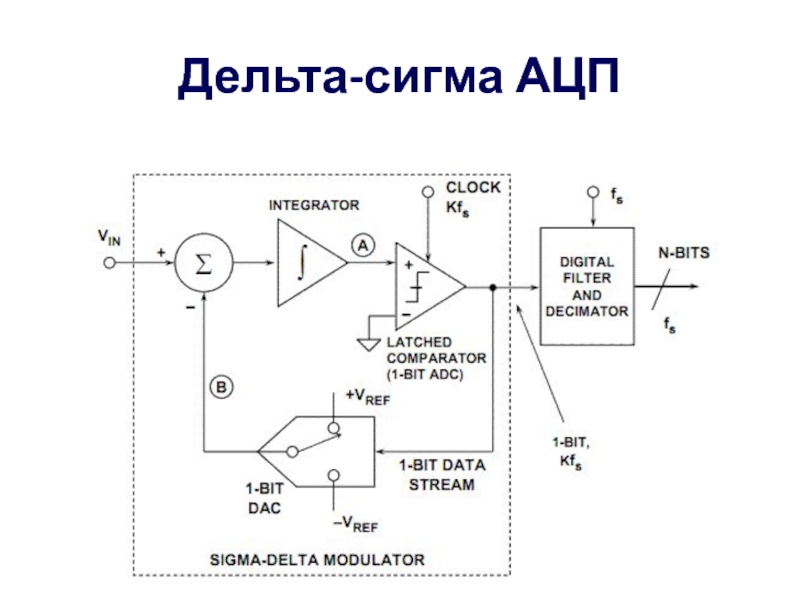
- 10. Дельта-сигма АЦП
- 11. Принцип действия данного АЦП несколько более сложен,
- 12. Слайд 12
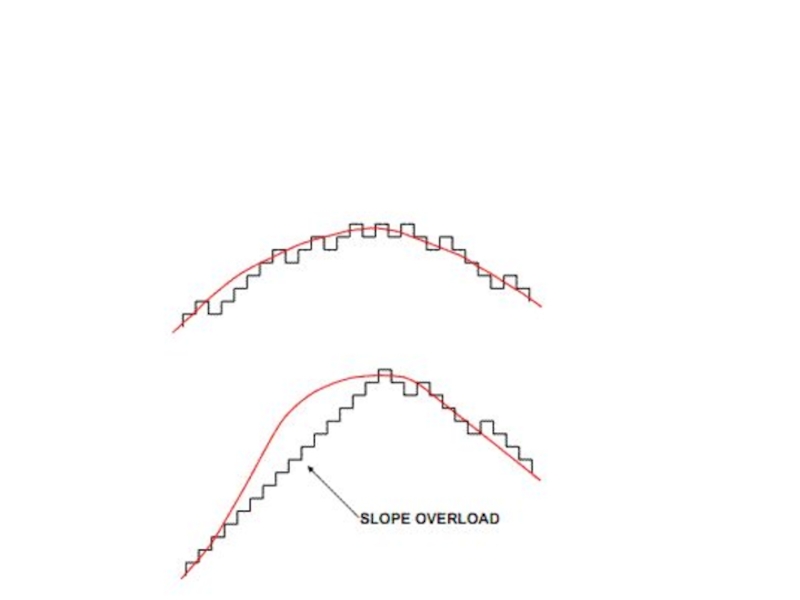
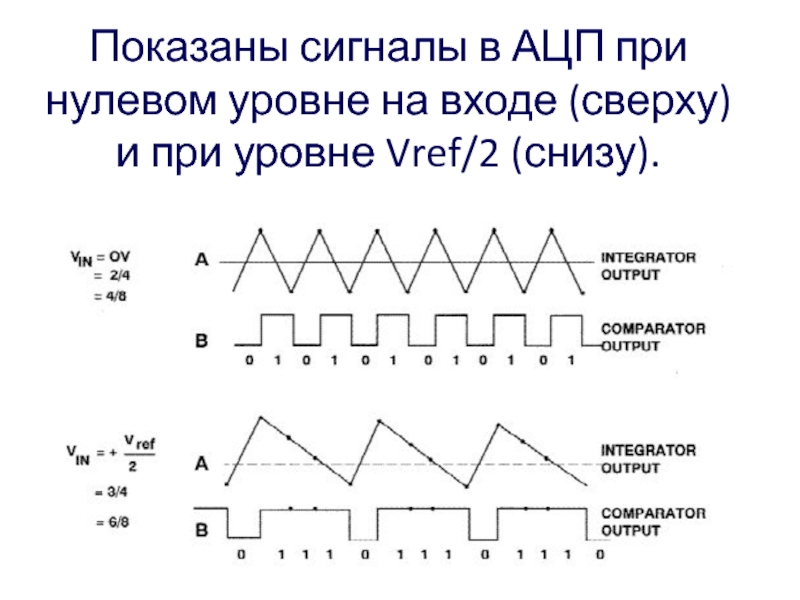
- 13. Показаны сигналы в АЦП при нулевом уровне на входе (сверху) и при уровне Vref/2 (снизу).
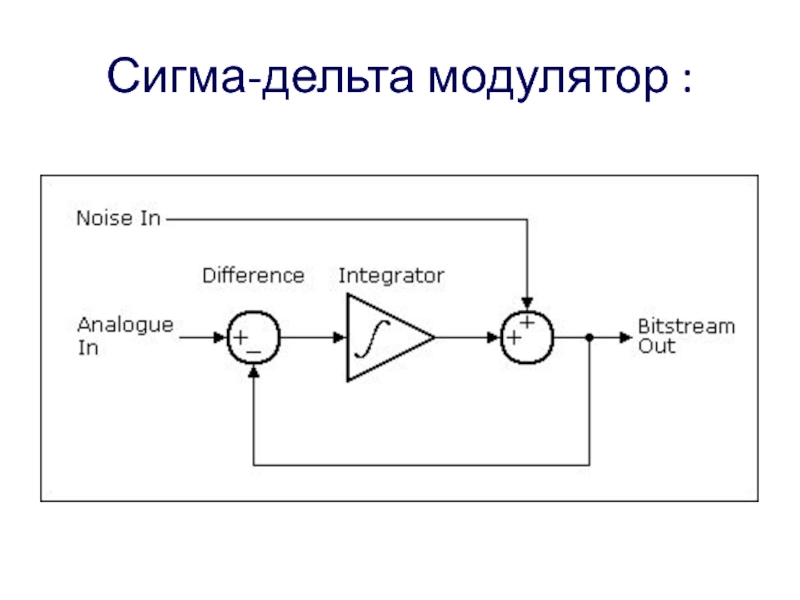
- 14. Сигма-дельта модулятор :
- 15. Здесь компаратор представлен как сумматор, который суммирует
- 16. Основным достоинством сигма-дельта АЦП является высокая точность,
- 17. Скачать презентанцию
АЦП параллельного преобразованияАЦП прямого преобразования получили широкое распространение в 1960-1970 годах, и стали производиться в виде интегральных схем в 1980-х. Они часто используются в составе «конвейерных» АЦП (в данной статье не
Слайды и текст этой презентации
Слайд 1Типы АЦП:
АЦП параллельного преобразования (прямого преобразования, flash ADC)
АЦП последовательного приближения
(SAR ADC)
Слайд 2АЦП параллельного преобразования
АЦП прямого преобразования получили широкое распространение в 1960-1970
годах, и стали производиться в виде интегральных схем в 1980-х.
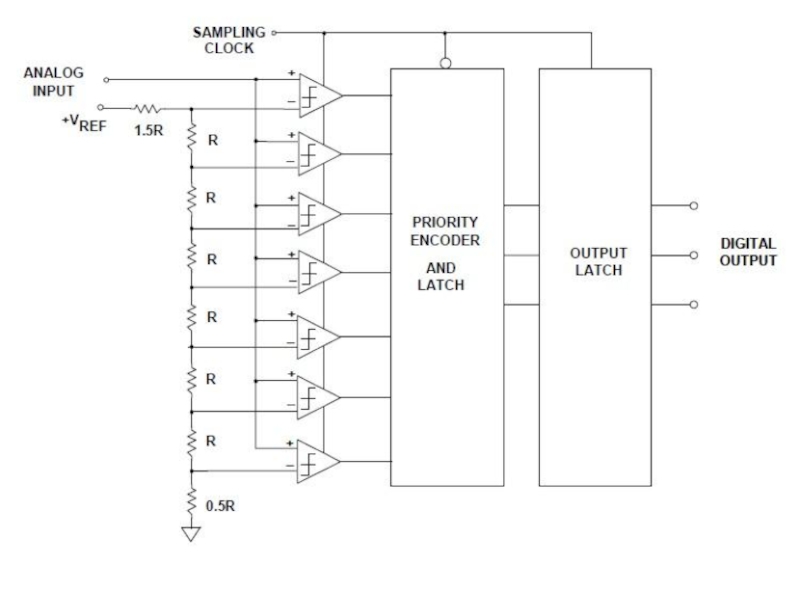
Они часто используются в составе «конвейерных» АЦП (в данной статье не рассматриваются), и имеют разрядность 6-8 бит при скорости до 1 GSPS.Слайд 4Принцип действия АЦП предельно прост: входной сигнал поступает одновременно на
все «плюсовые» входы компараторов, а на «минусовые» подается ряд напряжений,
получаемых из опорного путем деления резисторами R. Для схемы на рисунке этот ряд будет таким: (1/16, 3/16, 5/16, 7/16, 9/16, 11/16, 13/16) Uref, где Uref – опорное напряжение АЦП.Слайд 5АЦП последовательного приближения
АЦП последовательного приближения реализует алгоритм «взвешивания», восходящий еще
к Фибоначчи. В своей книге «Liber Abaci» (1202 г.) Фибоначчи
рассмотрел «задачу о выборе наилучшей системы гирь», то есть о нахождении такого ряда весов гирь, который бы требовал для нахождения веса предмета минимального количества взвешиваний на рычажных весах. Решением этой задачи является «двоичный» набор гирь.Слайд 6
Аналого-цифровой преобразователь последовательного приближения (SAR, Successive Approximation Register) измеряет величину
входного сигнала, осуществляя ряд последовательных «взвешиваний», то есть сравнений величины
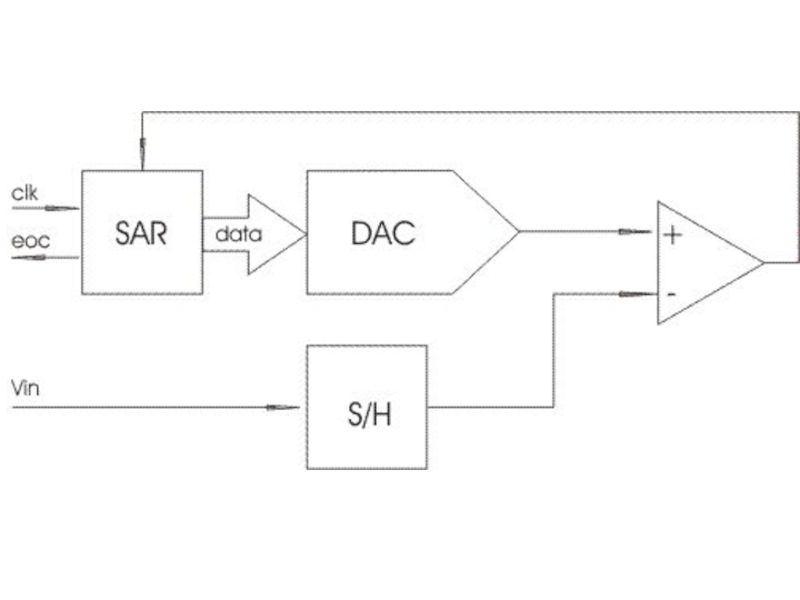
входного напряжения с рядом величин, генерируемых следующим образом: 1. на первом шаге на выходе встроенного цифро-аналогового преобразователя устанавливается величина, равная 1/2Uref (здесь и далее мы предполагаем, что сигнал находится в интервале (0 – Uref). 2. если сигнал больше этой величины, то он сравнивается с напряжением, лежащим посередине оставшегося интервала, т.е., в данном случае, 3/4Uref. Если сигнал меньше установленного уровня, то следующее сравнение будет производиться с меньшей половиной оставшегося интервала (т.е. с уровнем 1/4Uref). 3. Шаг 2 повторяется N раз. Таким образом, N сравнений («взвешиваний») порождает N бит результата.Слайд 8Таким образом, АЦП последовательного приближения состоит из следующих узлов:
Компаратор. Он
сравнивает входную величину и текущее значение «весового» напряжения
Цифро-аналоговый преобразователь (Digital
to Analog Converter, DAC). Он генерирует «весовое» значение напряжения на основе поступающего на вход цифрового кода.Регистр последовательного приближения (Successive Approximation Register, SAR). Он осуществляет алгоритм последовательного приближения, генерируя текущее значение кода, подающегося на вход ЦАП. По его названию названа вся данная архитектура АЦП.
Схема выборки-хранения (Sample/Hold, S/H). Для работы данного АЦП принципиально важно, чтобы входное напряжение сохраняло неизменную величину в течение всего цикла преобразования. Однако «реальные» сигналы имеют свойство изменяться во времени. Схема выборки-хранения «запоминает» текущее значение аналогового сигнала, и сохраняет его неизменным на протяжении всего цикла работы устройства.
Слайд 9
Достоинством устройства является относительно высокая скорость преобразования: время преобразования N-битного
АЦП составляет N тактов. Точность преобразования ограничена точностью внутреннего ЦАП
и может составлять 16-18 бит (сейчас стали появляться и 24-битные SAR ADC, например, AD7766 и AD7767).Слайд 11Принцип действия данного АЦП несколько более сложен, чем у других
типов АЦП. Его суть в том, что входное напряжение сравнивается
со значением напряжения, накопленным интегратором. На вход интегратора подаются импульсы положительной или отрицательной полярности, в зависимости от результата сравнения. Таким образом, данный АЦП представляет собой простую следящую систему: напряжение на выходе интегратора «отслеживает» входное напряжениеСлайд 15Здесь компаратор представлен как сумматор, который суммирует непрерывный полезный сигнал
и шум квантования.
Пусть интегратор имеет передаточную функцию 1/s. Тогда, представив
полезный сигнал как X(s), выход сигма-дельта модулятора как Y(s), а шум квантования как E(s), получаем передаточную функцию АЦП:
Y(s) = X(s)/(s+1) + E(s)s/(s+1)
То есть, фактически сигма-дельта модулятор является фильтром низких частот (1/(s+1)) для полезного сигнала, и фильтром высоких частот (s/(s+1)) для шума, причем оба фильтра имеют одинаковую частоту среза. Шум, сосредоточенный в высокочастотной области спектра, легко удаляется цифровым ФНЧ, который стоит после модулятора.