Логика.ppt

0 и 1.
Задача – разработать оптимальные правила обработки таких данных.
Джордж

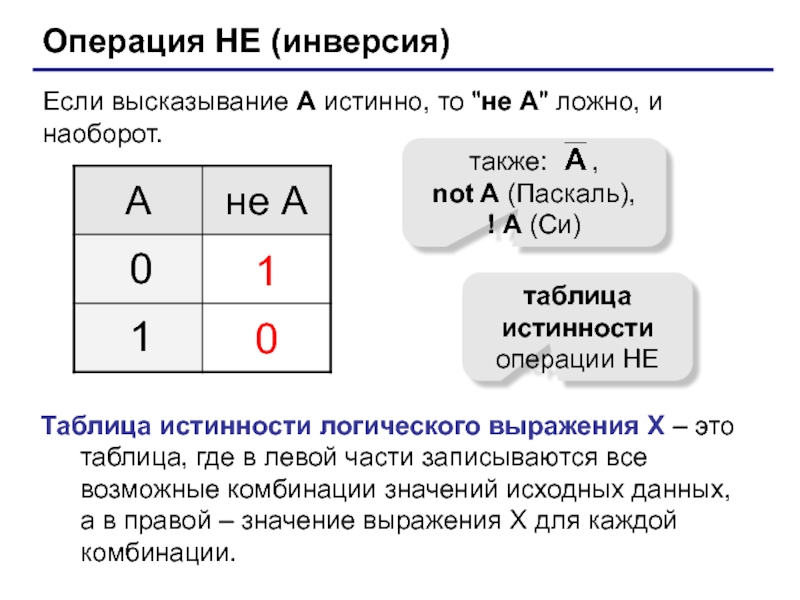
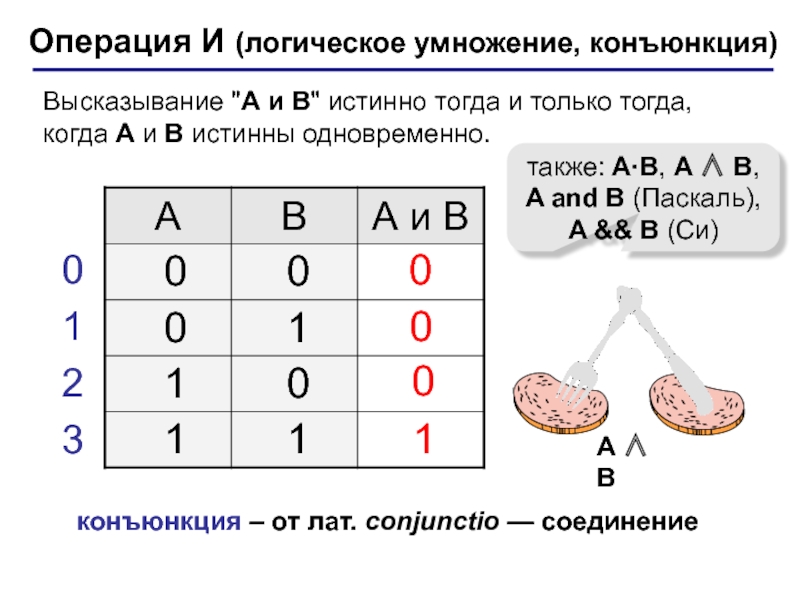
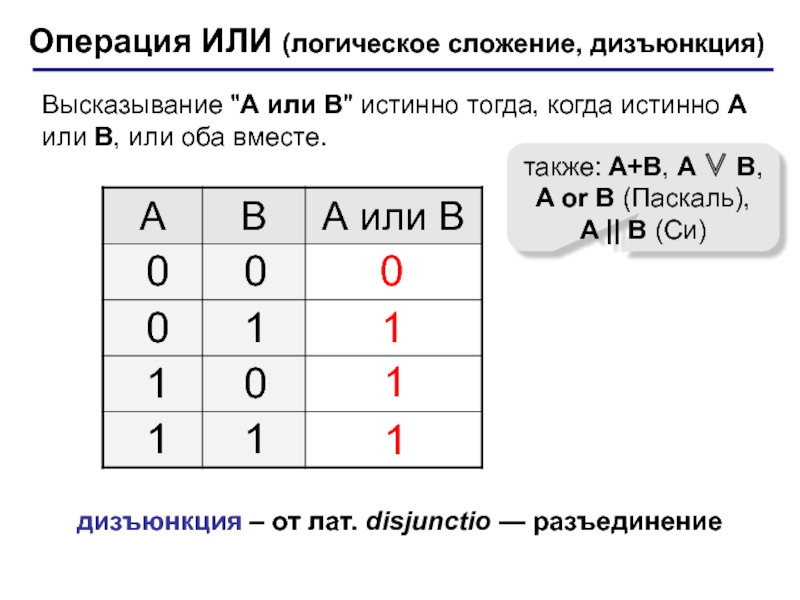
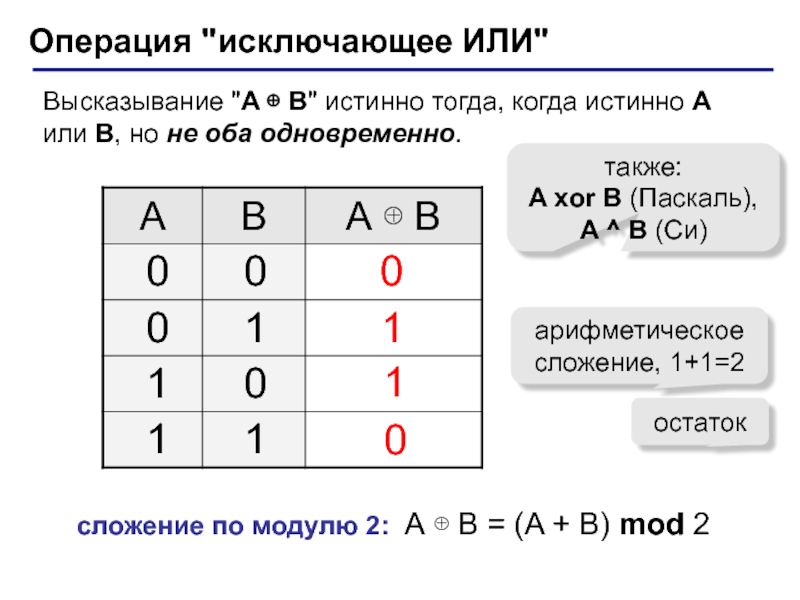
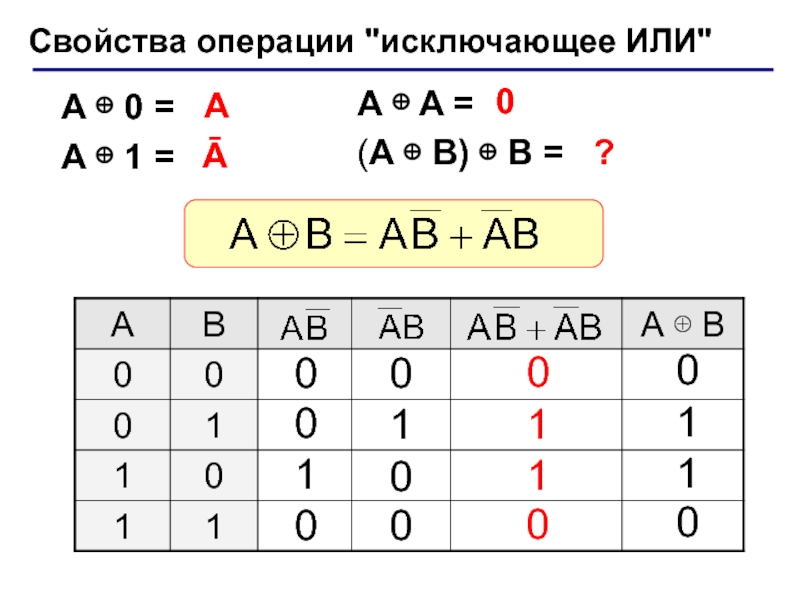
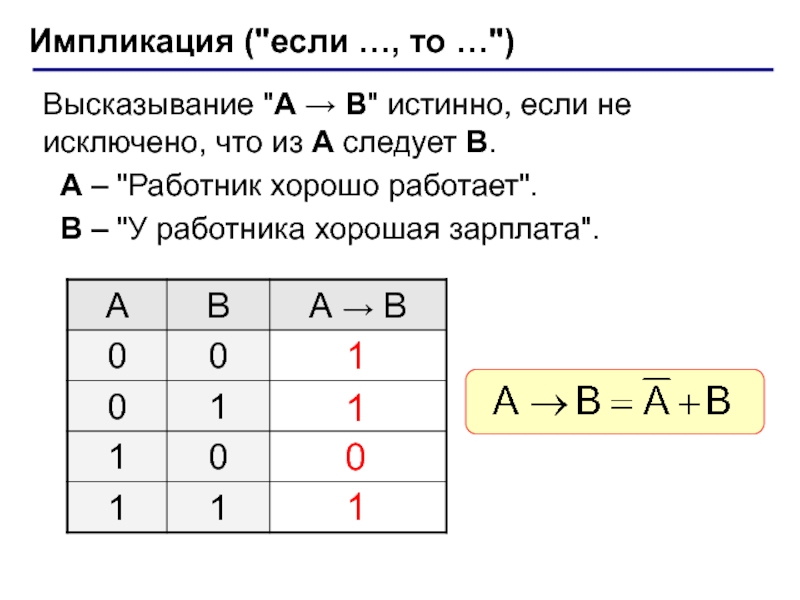
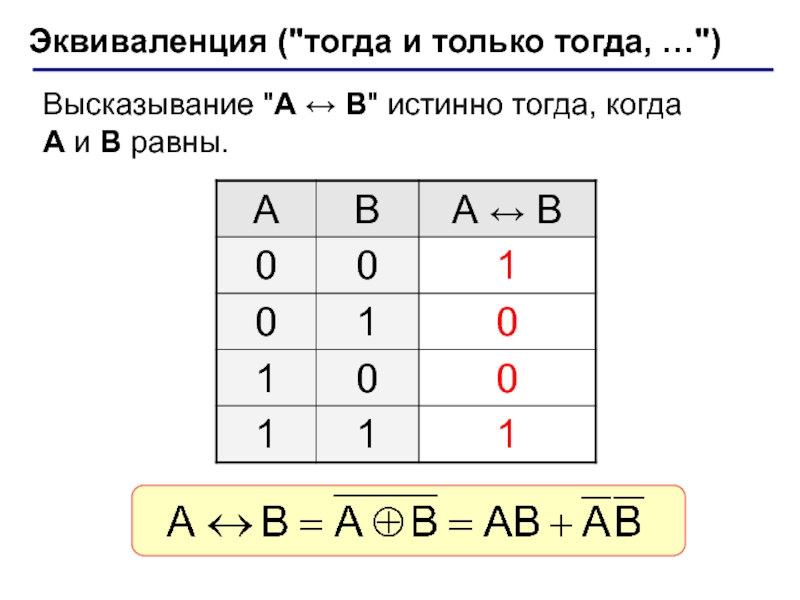
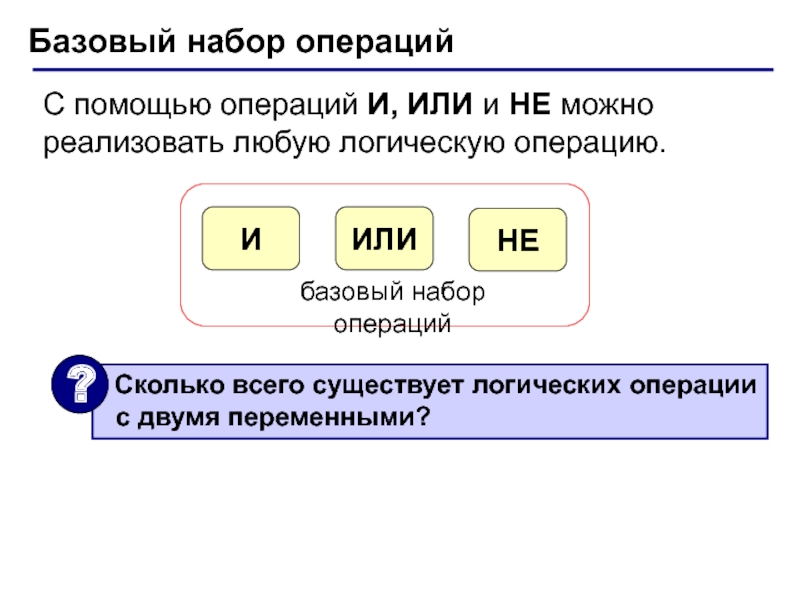
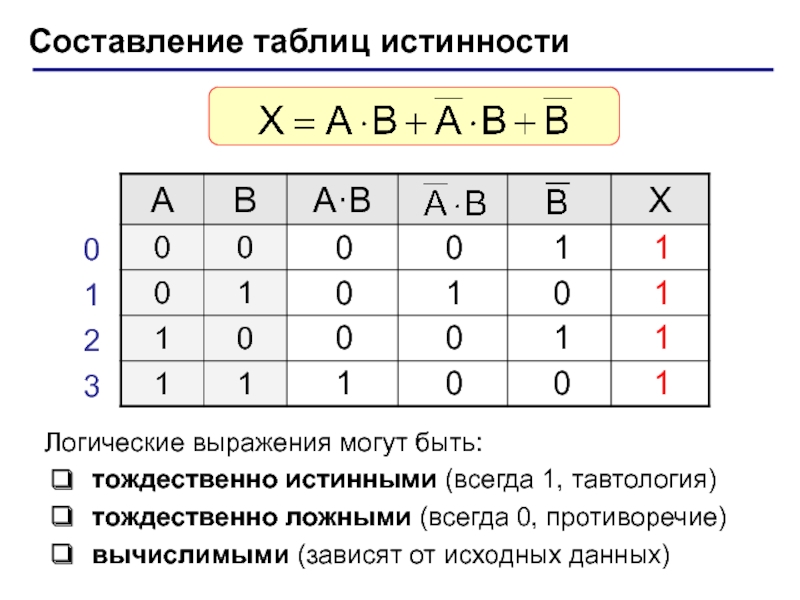
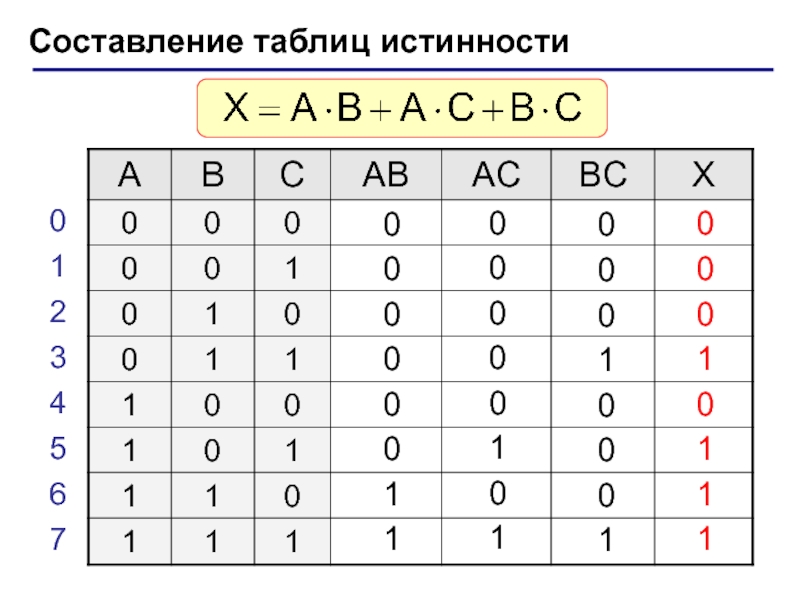
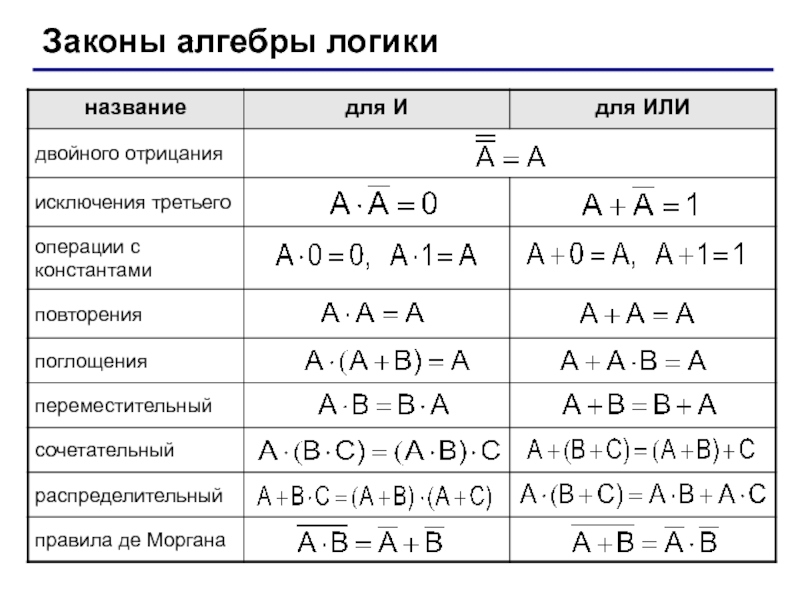
Буль разработал основы алгебры, в которой используются только 0 и 1 (алгебра логики, булева алгебра).
Почему "логика"? Результат выполнения операции можно представить как истинность (1) или ложность (0) некоторого высказывания.

однозначно сказать, истинно оно или ложно.
Высказывание или нет?
Сейчас идет дождь.
Жирафы

летят на север.
История – интересный предмет.
У квадрата – 10 сторон и все разные.
Красиво!
В городе N живут 2 миллиона человек.
Который час?

(элементарные)
Составные высказывания строятся из простых с помощью логических связок (операций)

"и", "или", "не", "если … то", "тогда и только тогда" и др.

A и B
A или не B
если A, то B
не A и B
A тогда и только
тогда, когда B

Сейчас идет дождь и открыта форточка.
Сейчас идет дождь или форточка закрыта.
Если сейчас идет дождь, то форточка открыта.
Сейчас нет дождя и форточка открыта.
Дождь идет тогда и только тогда, когда открыта форточка.

и наоборот.
1
0
0
1
таблица истинности операции НЕ
также: , not A (Паскаль),

! A (Си)

Таблица истинности логического выражения Х – это таблица, где в левой части записываются все возможные комбинации значений исходных данных, а в правой – значение выражения Х для каждой комбинации.

B (Паскаль), A && B (Си)
0
0
конъюнкция – от лат. conjunctio

— соединение

A ∧ B

Высказывание "A и B" истинно тогда и только тогда, когда А и B истинны одновременно.

B (Паскаль), A || B (Си)
1
1
дизъюнкция – от лат. disjunctio

— разъединение

Высказывание "A или B" истинно тогда, когда истинно А или B, или оба вместе.

А или B, но не оба одновременно.
0
0
также: A xor B

(Паскаль), A ^ B (Си)

1

1

сложение по модулю 2: А ⊕ B = (A + B) mod 2

арифметическое сложение, 1+1=2

остаток

"исключающее ИЛИ"
A ⊕ 0 =
A ⊕ 1 =
A
0
Ā
?

не исключено, что из А следует B.
A – "Работник

хорошо работает".
B – "У работника хорошая зарплата".

1

1

1

0

тогда, когда А и B равны.

реализовать любую логическую операцию.

из них исправны.
A – "Датчик № 1 неисправен".

B – "Датчик № 2 неисправен".
C – "Датчик № 3 неисправен".
Аварийный сигнал:
X – "Неисправны два датчика".

X – "Неисправны датчики № 1 и № 2" или
"Неисправны датчики № 1 и № 3" или
"Неисправны датчики № 2 и № 3".

логическая формула

ложными (всегда 0, противоречие)
вычислимыми (зависят от исходных данных)

через И, ИЛИ и НЕ:
Шаг 2. Раскрыть инверсию сложных выражений

по формулам де Моргана:
Шаг 3. Используя законы логики, упрощать выражение, стараясь применять закон исключения третьего.

(0, 1, 1)
или
A=1, B=0, C=1
K=1, L=1,
M и N –

любые
4 решения

M=1, L=1, N=1,
K – любое
2 решения

K=1, L=1, M=0,
N – любое
2 решения

= 1.
Шаг 2. Для каждой из них записать логическое выражение,

которое истинно только для этой строки.
Шаг 3. Сложить эти выражения и упростить результат.

распределительный

исключения третьего

исключения третьего

распределительный

где X = 0.
Шаг 2. Для каждой из них записать

логическое выражение, которое истинно только для этой строки.
Шаг 3. Сложить эти выражения и упростить результат, который равен .
Шаг 4. Сделать инверсию.

или ИЛИ-НЕ.
И:
НЕ:
ИЛИ:

хранить 1 бит информации (1 или 0). Строится на 2-х

элементах ИЛИ-НЕ или на 2-х элементах И-НЕ.

основной
выход

вспомогательный
выход

reset, сброс

set, установка

обратные связи

1

1

0

0

1

1

числа.
0 0
0

1

0 1

1 0

числа с переносом из предыдущего разряда.

Σ
сумма
перенос
перенос

обсудили за закрытыми дверями проекты договора, представленные каждой из стран.

Отвечая затем на вопрос журналистов: "Чей именно проект был принят?", министры дали такие ответы:
Россия — "Проект не наш (1), проект не США (2)";
США — "Проект не России (1), проект Китая (2)";
Китай — "Проект не наш (1), проект России (2)".
Один из них оба раза говорил правду; второй – оба раза говорил неправду, третий один раз сказал правду, а другой раз — неправду. Кто что сказал?

проект России (?)

–

+

–

–

+

+

проект США (?)

+

–

проект Китая (?)

+

–

+

+

+

+

Лариса. У них разные профессии и они живут в разных

городах: одна в Ростове, вторая – в Париже и третья – в Москве. Известно, что
Даша живет не в Париже, а Лариса – не в Ростове,
парижанка – не актриса,
в Ростове живет певица,
Лариса – не балерина.

0

0

0

0

1

0

0

0

1

0

0

1

1

0

1

0

0

1

Много вариантов.
Есть точные данные.

В каждом доме живет по одному человеку отличной от другого

национальности. Каждый жилец пьет только один определенный напиток, курит определенную марку сигарет и держит животное. Никто из пяти человек не пьет одинаковые напитки, не курит одинаковые сигареты и не держит одинаковых животных.
Известно, что:
Англичанин живет в красном доме.
Швед держит собаку.
Датчанин пьет чай.
Зеленой дом стоит слева от белого.
Жилец зеленого дома пьет кофе.
Человек, который курит Pallmall, держит птицу.
Жилец среднего дома пьет молоко.
Жилец из желтого дома курит Dunhill.
Норвежец живет в первом доме.
Курильщик Marlboro живет около того, кто держит кошку.
Человек, который содержит лошадь, живет около того, кто курит Dunhill.
Курильщик Winfield пьет пиво.
Норвежец живет около голубого дома.
Немец курит Rothmans.
Курильщик Marlboro живет по соседству с человеком, который пьет воду.
Вопрос: У кого живет рыба?

если корабль A вышел в море, то корабль C –

нет.
2. В море вышел корабль B или корабль C, но не оба вместе.
Определить, какие корабли вышли в море.

… если корабль A вышел в море, то корабль C – нет.

1. Неверно, что если корабль A вышел в море, то корабль C – нет.

2. В море вышел корабль B или корабль C, но не оба вместе.

Решение:

«Память не могла выйти из строя». Его сын предположил, что

сгорел процессор, а винчестер исправен. Мастер по ремонту сказал, что с процессором все в порядке, а память неисправна. В результате оказалось, что двое из них сказали все верно, а третий – все неверно. Что же сломалось?

Решение:

A – неисправен процессор, B – память, C – винчестер

хозяин:

сын:

мастер:

Если ошибся хозяин:

Если ошибся сын:

Если ошибся мастер:

В общем случае: