Слайд 1Лекція 2. Динаміка матеріальної точки і твердого тіла
1. Перший
закон Ньютона. Інерціальні системи.
2. Другий закон Ньютона.
3. Третій закон Ньютона.
4.
Принцип відносності Галілея.
5. Сили. Застосування законів Ньютона.
6. Кінематика абсолютно твердого тіла. Плоский рух.
7. Рух центра мас твердого тіла.
8. Обертання навколо нерухомої осі.
9. Момент інерції. Тензор інерції.
10. Кінетична енергія обертального руху тіла та при плоскому русі.
Слайд 2Перший закон Ньютона. Інерціальні системи.
І з-н Ньютона: Будь-яке тіло знаходиться
в стані спокою чи рівномірного прямолінійного руху, поки дія з
боку інших тіл не спричинить зміну цього стану.
Система відліку, в якій виконується І закон Ньютона, називається інерціальною. Система відліку, в якій не виконується І закон Ньютона, називається неінерціальною.
Будь-яка система, що рухається рівномірно (=const) і прямолінійно відносно інерціальної системи, також буде інерціальною.
Слайд 3Маса та імпульс.
Інертність тіла – опір спробам змінити стан його
руху.
Кількісною характеристикою, яка характеризує інертність, виступає маса тіла.
Фізична величина, яка
є мірою інертності матеріальної точки, називається інертною масою mi.
Фізична величина, яка є мірою гравітаційної взаємодії між тілами, називається гравітаційною масою mg.
Експериментально встановлено, що mi = mg.
Маса – скалярна, адитивна величина: m=Σmi.
Слайд 4Маса та імпульс.
Якщо два тіла взаємодіють через зіткнення, то їхні
швидкості будуть мати зміну Δ1 і Δ2, причому виконується співвідношення:
Отже m1Δ1 = -m2Δ2 або Δp1 = -Δp2 , де p = m називається імпульсом тіла.
Тіло розглядають як сукупність матеріальних точок, так що маса
Слайд 5Другий закон Ньютона
Ця формула використовується для знаходження
маси тіла.
Сила – це векторна величина, що є мірою механічної
дії
на тіло з боку інших тіл, внаслідок якої тіло отримує
прискорення або змінює свою форму і розміри.
Сила характеризується числовим значенням,
напрямком у просторі і точкою прикладання.
Слайд 6Одиниці розмірностей фізичних величин
Система СІ (Система Інтернаціональна): довжина – 1
м, маса – 1 кг, час – 1 с, струм
– ампер, сила світла – кандела, одиниця температури – 1 К, кількість речовини – моль.
Формула F = mw дає одиницю сили 1 Н, дія якої на масу 1 кг дає прискорення 1 м/с2.
Довжина меридіана Землі 40 000 000 м.
Секунда – час, який дорівнює 9192631770 періодам випромінювання між двома надтонкими рівнями основного стану атома 133Cs. В одному році 31556925,9747 с.
Слайд 7Одиниці розмірностей фізичних величин
Дольні та кратні одиниці: деци – 10-1,
санти – 10-2, мілі – 10-3,
мікро – 10-6, нано
- 10-9, піко – 10-12, фемто – 10-15;
дека -10, гекто – 102, кіло – 103, Мега – 106, Гіга – 109,
Тера – 1012.
Сукупність одиниць утворює певну систему.
Розмірність довільної фізичної величини визначається через основні одиниці (прискорення – м/с2).
Фізичні закони не залежать від вибору системи одиниць. В довільній формулі розмірності зліва і справа строго однакові.
Слайд 8Третій закон Ньютона
Дія двох тіл одне на інше називається взаємодією.
Якщо перше тіло діє на друге з силою F12, то
і друге тіло діє на перше з силою F21, причому ці сили рівні за величиною і протилежні за напрямком:
F12 = - F21
Отже, сили виникають попарно. Це і є ІІІ закон Ньютона.
Третій закон Ньютона виконується як при контактній взаємодії, так і при взаємодії відділених тіл (через гравітаційне, електростатичне чи інше поле).
Слайд 9Третій закон Ньютона
Сукупність матеріальних точок, які розглядаються як єдине ціле,
називається механічною системою. Механічна система, на яку не діють зовнішні
сили, називається замкненою.
- замкнена система.
Слайд 10Принцип відносності Галілея
x, x’
y
z
y’
z’
O
O’
ot
x
x’
P
x=x’ + ot
y=y’
z=z’
Слайд 11Принцип відносності Галілея
Продиференціюємо за часом вираз
Отримаємо
Отже, прискорення однакове у всіх
інерціальних
системах відліку.
Основне рівняння механіки F=ma містить лише
прискорення, тому рівняння динаміки однакові у
всіх інерціальних системах.
Слайд 12Сили
Є 4 види взаємодій: гравітаційна, електромагнітна, сильна, слабка. Наприклад:
Пружні сили
та сили тертя не є фундаментальни-ми, а відносяться до електромагнітних.
Слайд 13Пружні сили
Fпр ~ x
Fпр =-kx – Закон Гука
Деформація розтягу
Слайд 15Сила тертя
Зовнішнє тертя – між поверхнями двох тіл, внутрішнє –
між частинками одного і того ж тіла (рідина, газ).
Fт =
kFн
Сила тертя ковзання не
залежить від площі дотику
поверхонь і пропорціональна
силі нормального тиску.
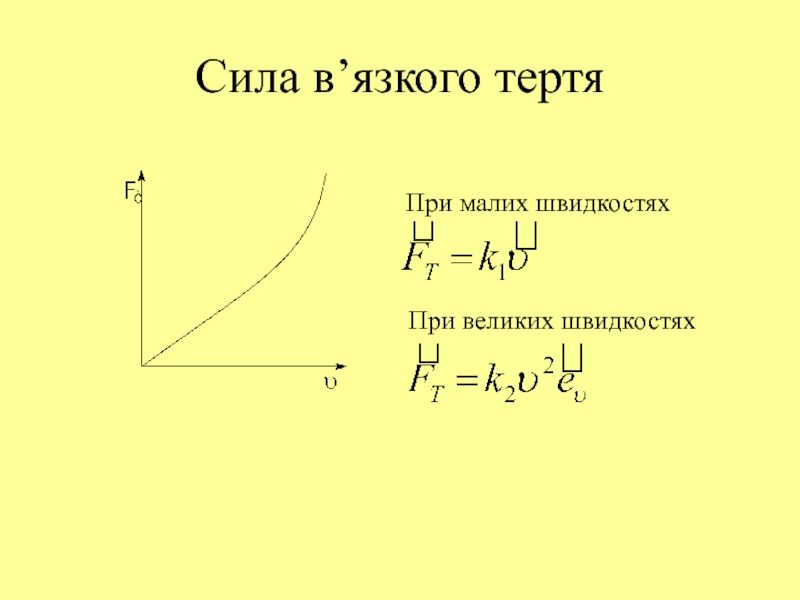
Слайд 16Сила в’язкого тертя
При малих швидкостях
При великих швидкостях
Слайд 17Сила тяжіння і вага
- Сила тяжіння
Тіло діє на опору з
силою
- вага тіла
Коли тіло рухається з прискоренням, тоді
Тепер сила, що
діє на опору і дорівнює вазі,
- при
- невагомість.
Слайд 18Застосування законів Ньютона
Тіло рухається по похилій площині.
Fr = FT +
Fn
x
Проекція на вісь x:
Звідси
Формула справедлива при w > 0
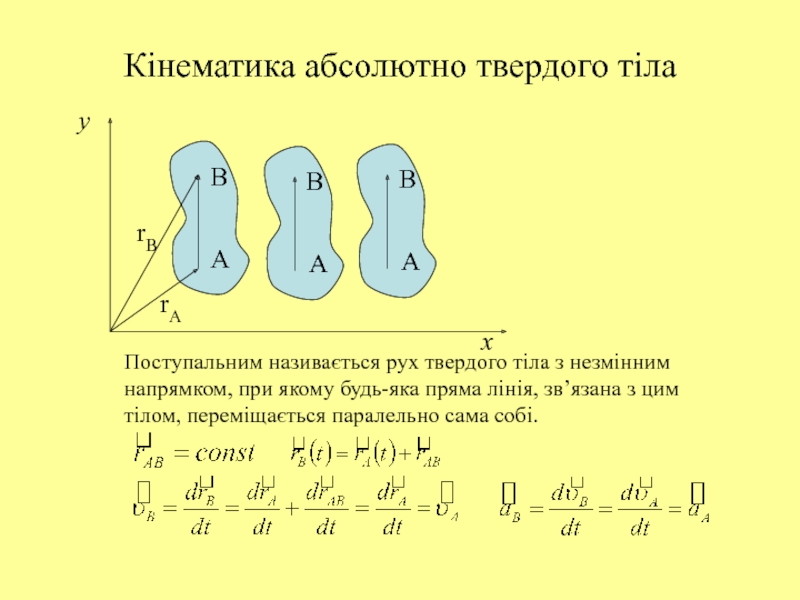
Слайд 19Кінематика абсолютно твердого тіла
y
x
A
A
B
B
rA
rB
A
B
Поступальним називається рух твердого тіла з незмінним
напрямком, при якому будь-яка пряма лінія, зв’язана з цим
тілом, переміщається
паралельно сама собі.
Слайд 20Кінематика абсолютно твердого тіла
Обертальний рух
1 ≠ 2
S1 ≠ S2
a1 ≠
a2
Кутовий шлях φ однаковий
для всіх точок
Слайд 21Зв’язок між лінійними і кутовими характеристиками
Слайд 22Плоский рух
Довільний рух тіла на площині може бути зображений як
сума поступального і обертального рухів:
При цьому о однакове для всіх
точок, а ’ різне.
Для циліндра, що котиться
Елементарне переміщення при плоскому русі можна зобразити, як поворот навколо миттєвої осі, положення якої змінюється з часом.
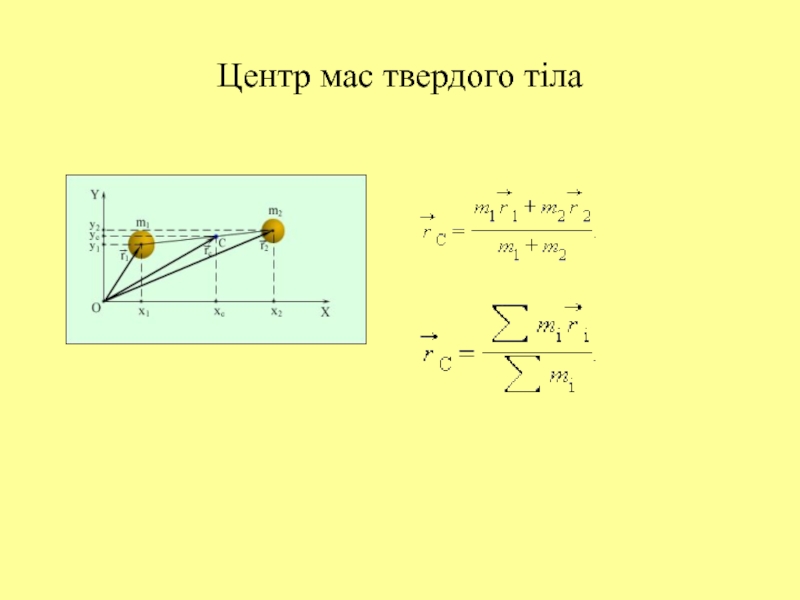
Слайд 24Рух центра мас твердого тіла
Уявимо тверде тіло як суму елементарних
мас, на які діють як зовнішні, так і внутрішні сили:
fi
– внутрішні, Fi – зовнішні сили.
-Рух центра мас під дією суми сил
Радіус-вектор центра мас
Слайд 25Обертання навколо нерухомої осі
- Момент імпульсу
- момент сили
Li
ri
mi
Ri
Слайд 26Для симетричних тіл
Обертання навколо нерухомої осі
Є 3 головні осі
інерції. В загальному випадку I1≠I2≠I3.
Стійким є обертання навколо осей з
Imin і Imax.
обруч
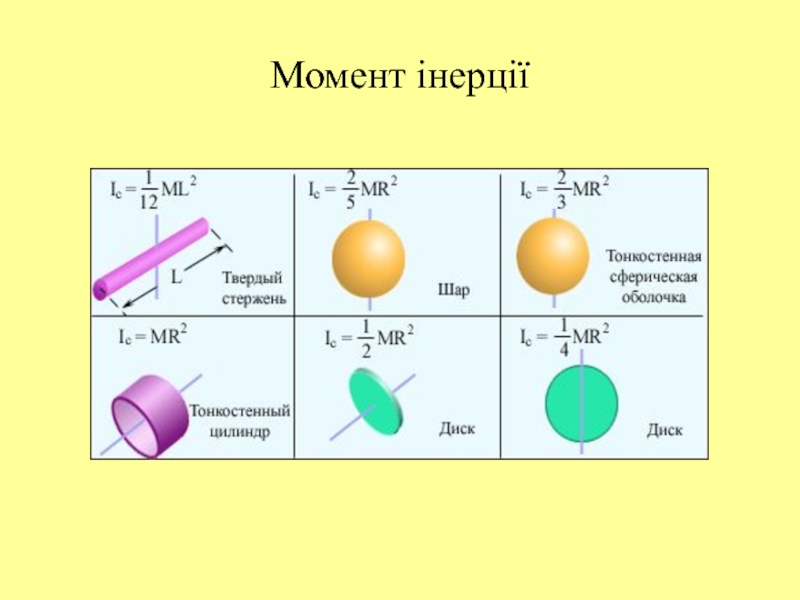
Слайд 27Момент інерції
Для диску (циліндра) навколо осі обертання
Слайд 28Момент інерції
Теорема Штейнера: при обертанні тіла навколо осі О’О’
I = Ic + ma2
Для диску (циліндра) при a =
R
a
O
C
Ri
Ri
'
Δmi
- вісь через центр мас
'
Слайд 30Тензор інерції
Для несиметричних тіл вектори L і не паралельні.
Для симетричних тіл недіагональні елементи відсутні
Слайд 32Кінетична енергія обертального руху
ri
mi
Ri
fi
Fi
Слайд 33Кінетична енергія при плоскому русі
Слайд 34Застосування законів динаміки твердого тіла
Сумарний момент сили тяжіння відносно деякої
точки
Ця величина дорівнює нулю відносно центра мас.
Точка, відносно якої момент
сил тяжіння дорівнює нулю,
називається центром ваги.
Тіло буде в спокої, якщо Fзовн = 0 і Mзовн = 0.
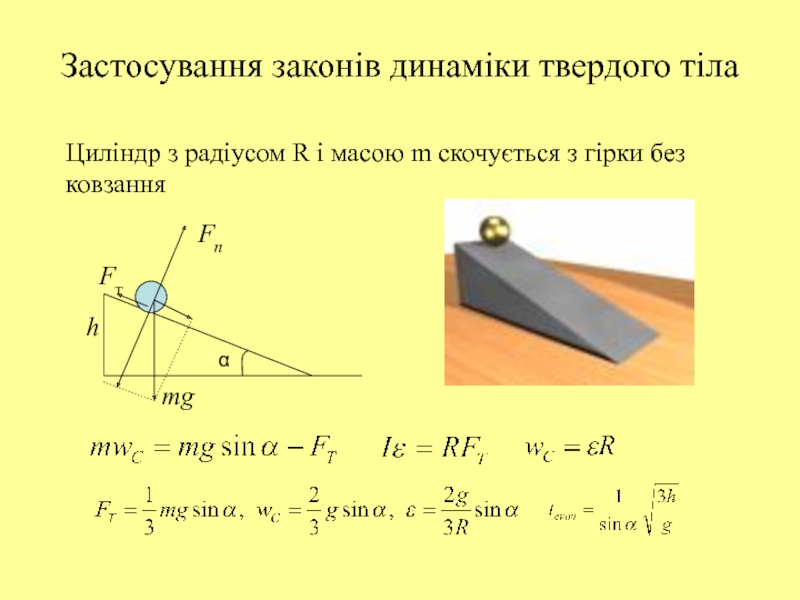
Слайд 35Застосування законів динаміки твердого тіла
Циліндр з радіусом R і масою
m скочується з гірки без
ковзання
h
mg
Fn
Fт
Слайд 36Застосування законів динаміки твердого тіла
Другий метод розв’язування
Повна енергія залишається сталою.
На
початку потенціальна енергія U = mgh
Вкінці кінетична енергія