Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Типы распределения признаков
Содержание
- 1. Типы распределения признаков
- 2. Нормальное распределениеРаспределение симметрично, причем крайние значения (наибольшие
- 3. Биномиальное распределениеХарактеризует поведение дискретных признаков, выраженных целыми
- 4. Распределение ПуассонаЭто вариант описания стохастического поведения дискретных
- 5. Распределение ПуассонаВ последующие пять лет часть из
- 6. Альтернативное распределениеРаспределение дискретной случайной величины, имеющей лишь
- 7. Полиномиальное распределениеНаблюдается для качественных признаков, имеющих не
- 8. Оценка генеральных параметровРаспределение – это соотношение между
- 9. СледствияВсе варианты лежат в интервале плюс-минус бесконечность.
- 10. СледствияМежду M − 1.96S и М +
- 11. СледствияС вероятностью P = 0.99 значение новой
- 12. Генеральная совокупностьГенеральная совокупность – все варианты одного
- 13. Ошибка репрезентативностиОтличия значений выборочных параметров от генеральных
- 14. Доверительный интервалГенеральная средняя находится в диапазоне Mвыбор.
- 15. Доверительный интервалВ соответствии с законом нормального распределения
- 16. Определение точности опытаЭто отношение ошибки средней к
- 17. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Нормальное распределение
Распределение симметрично, причем крайние значения (наибольшие и наименьшие) появляются
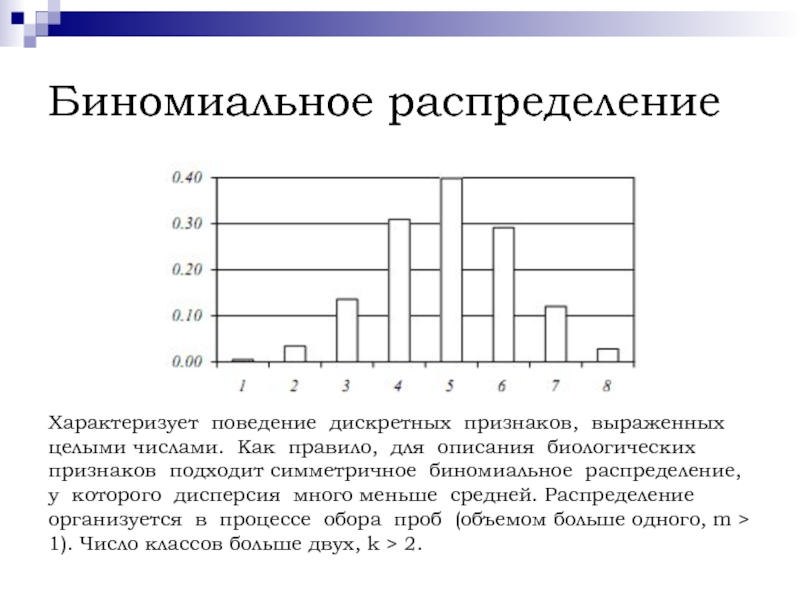
Слайд 3Биномиальное распределение
Характеризует поведение дискретных признаков, выраженных целыми числами. Как правило,
для описания биологических признаков подходит симметричное биномиальное распределение, у которого
дисперсия много меньше средней. Распределение организуется в процессе обора проб (объемом больше одного, m > 1). Число классов больше двух, k > 2.Слайд 4Распределение Пуассона
Это вариант описания стохастического поведения дискретных количественных признаков для
случаев, когда вероятность элементарных альтернативных событий неодинакова, одно из них
наблюдается заметно чаще другого (p << q). Закон Пуассона описывает редкие события, происходящие 1, 2, 3 и т. д. раз на сотни и тысячи обычных событий. Поведение биологических объектов, соответствующее закону Пуассона, наблюдается в том случае, когда по пробам случайно распределены редкие объекты.Слайд 5Распределение Пуассона
В последующие пять лет часть из них отлавливали повторно:
7 экз. по одному разу, 7 – по два, 2
– по три, 1 экз. – четыре раза, 15 экз. окольцованных птиц повторно не попадались. Число классов составляет k = 4, интервал dx = 1. Асимметрия в частотах встречаемости птиц позволяет предполагать распределение Пуассона.Слайд 6Альтернативное распределение
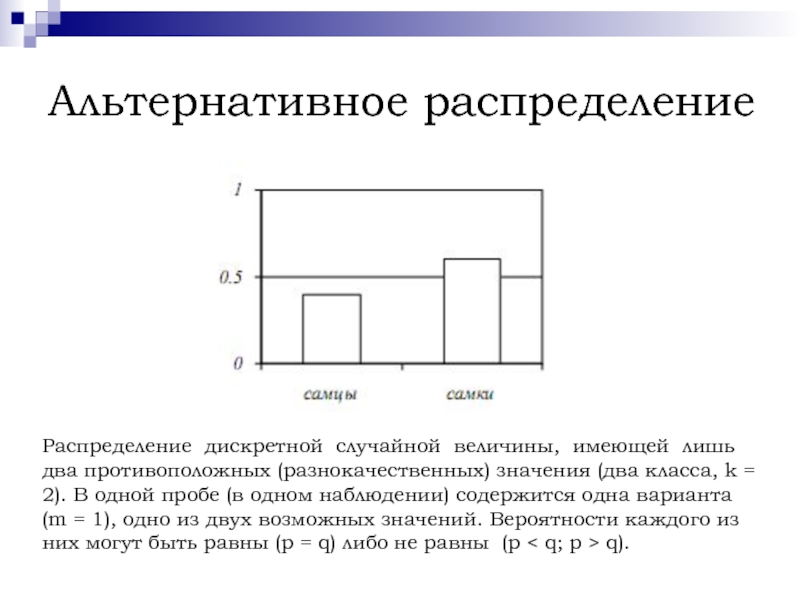
Распределение дискретной случайной величины, имеющей лишь два противоположных (разнокачественных)
значения (два класса, k = 2). В одной пробе (в
одном наблюдении) содержится одна варианта (m = 1), одно из двух возможных значений. Вероятности каждого из них могут быть равны (p = q) либо не равны (p < q; p > q).Слайд 7Полиномиальное распределение
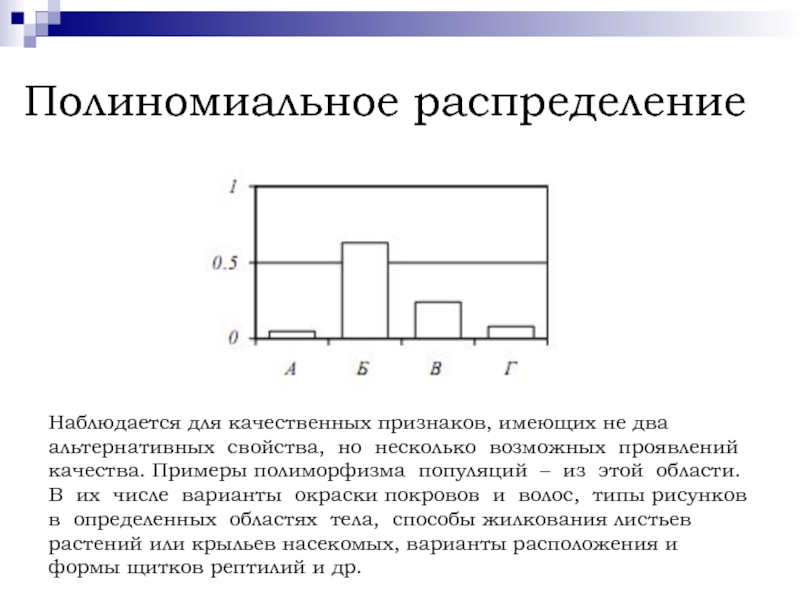
Наблюдается для качественных признаков, имеющих не два альтернативных свойства,
но несколько возможных проявлений качества. Примеры полиморфизма популяций – из
этой области. В их числе варианты окраски покровов и волос, типы рисунков в определенных областях тела, способы жилкования листьев растений или крыльев насекомых, варианты расположения и формы щитков рептилий и др.Слайд 8Оценка генеральных параметров
Распределение – это соотношение между значениями случайной величины
и частотой их встречаемости.
Вероятность (статистическая, или частость) – численная мера
возможного, определяется как отношение числа вариант (исходов испытаний) определенного вида к общему числу вариант (опытов).Слайд 9Следствия
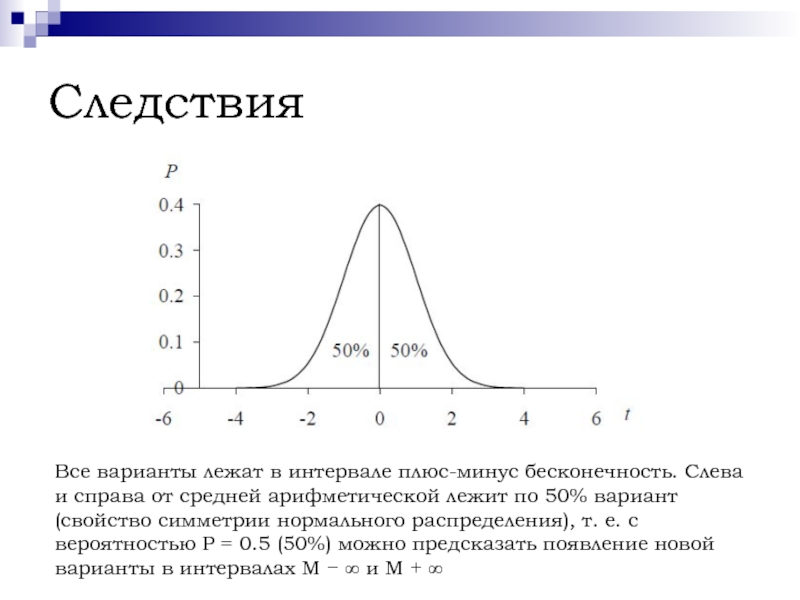
Все варианты лежат в интервале плюс-минус бесконечность. Слева и справа
от средней арифметической лежит по 50% вариант (свойство симметрии нормального
распределения), т. е. с вероятностью P = 0.5 (50%) можно предсказать появление новойварианты в интервалах M − ∞ и M + ∞
Слайд 10Следствия
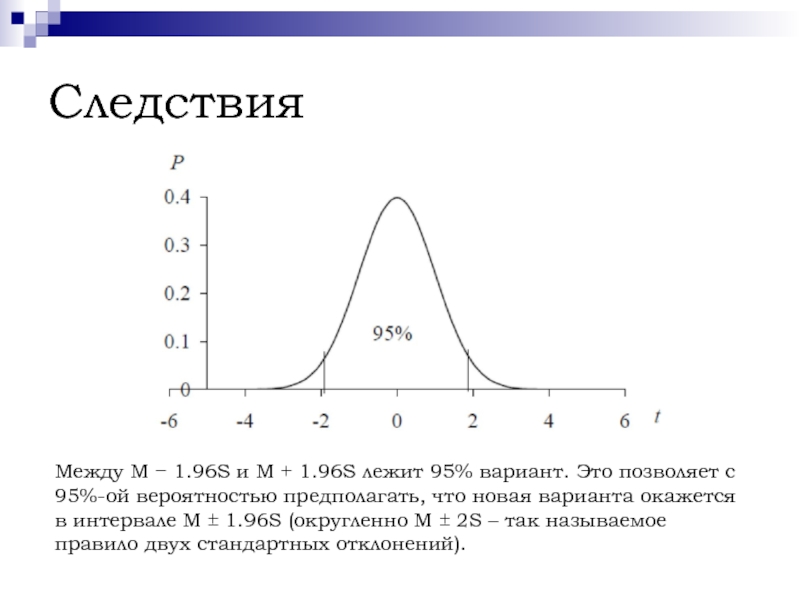
Между M − 1.96S и М + 1.96S лежит 95%
вариант. Это позволяет с
95%-ой вероятностью предполагать, что новая варианта
окажется в интервале М ± 1.96S (округленно М ± 2S – так называемое правило двух стандартных отклонений).Слайд 11Следствия
С вероятностью P = 0.99 значение новой варианты будет заключено
в пределах М ± 2.58S и с вероятностью P =
0.999 – в интервале М ± 3.3S.Термин «доверительная вероятность P = 0.95» означает, что, согласно принятому допущению, 95% вариант достаточно полно характеризуют изучаемое явление.
Уровень значимости – это тот теоретический процент значений нормального распределения, который можно отбросить, не учитывать, дабы с меньшими усилиями получить основную информацию об изучаемом явлении.
Для практического понимания достаточно знать, что уровень значимости – это вероятность ожидаемой ошибки наших выводов, вероятность того, что данный статистический вывод не верен.
Слайд 12Генеральная совокупность
Генеральная совокупность – все варианты одного типа.
Выборочная совокупность,
выборка – это множество вариант одного типа, ограниченное способом отбора
из генеральной совокупности.Чем меньше объем выборок, тем менее точным будут выборочные оценки генеральных параметров, и, напротив, чем больше выборка, тем ближе выборочные средние и дисперсии лежат к генеральным значениям (закон больших чисел).
Слайд 13Ошибка репрезентативности
Отличия значений выборочных параметров от генеральных называются ошибкой репрезентативности
данного параметра.
Величина ошибки тем больше, чем больше варьирование признака (S)
и чем меньше выборка (n). Вычисленные значения ошибок подставляют к соответствующим параметрам со знаками плюс-минус (параметр ± ошибка) и в такой форме представляют в научных отчетах и публикациях.
Слайд 14Доверительный интервал
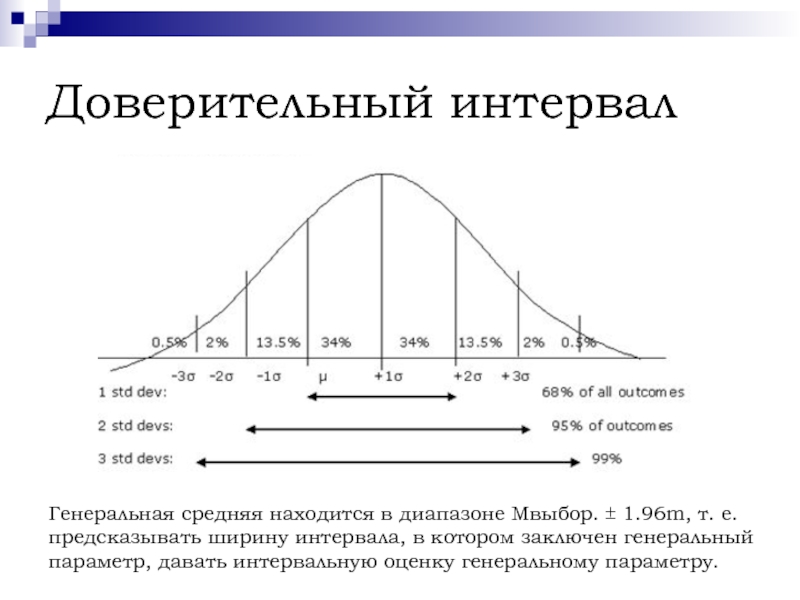
Генеральная средняя находится в диапазоне Mвыбор. ± 1.96m, т.
е.
предсказывать ширину интервала, в котором заключен генеральный
параметр, давать
интервальную оценку генеральному параметру. Слайд 15Доверительный интервал
В соответствии с законом нормального распределения можно ожидать, что
генеральный параметр (истинное значение) окажется в интервале от М −
tm до М + tm,где m – ошибка средней арифметической,
t – квантиль распределения Стьюдента при данном числе
степеней свободы (df ) и уровне значимости (обычно α = 0.05).
Доверительный интервал – это интервал значений изучаемого признака, в котором с той или иной вероятностью находится значение генерального параметра.
Слайд 16Определение точности опыта
Это отношение ошибки средней к самой средней арифметической,
выраженное в процентах
Точность считается хорошей, если ε меньше 3%, и
удовлетворительной при 3 < ε < 5%где п – объем выборки,
t – граничное значение из таблицы распределения Стьюдента, соответствующее принятому уровню значимости при планируемом объеме выборки,
CV – приблизительное значение коэффициента вариации (%),
ε – планируемая точность оценки (погрешности) (%).