Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ТНиС 04
Содержание
- 1. ТНиС 04
- 2. Исследование политропных процессов 1. Уравнение процесса
- 3. Преобразование выражения I закона термодинамикиУмножим полученное
- 4. Уравнение политропных процессов Разделим переменные, поделив уравнение
- 5. Соотношения между параметрами На предыдущем слайде за
- 6. Работа и теплота4. Изменение внутренней энергии: Δu=cvΔT.
- 7. Показатель политропы и энергетический коэффициент Политропную
- 8. Обобщающее значение политропных процессов Уравнение политропных
- 9. Три группы политропных процессов На следующем слайде
- 10. pv - диаграмма политропных процессовpn=-∞v=сonstn=0p=сonstn=1T=сonstn=kpvk=сonstn=+∞v=сonstΔu>0Δu0q
- 11. Энтропия идеального газа Обозначим через дифференциал энтропии
- 12. Изменение энтропии в термодинамических процессах Проинтегрировав
- 13. Изображение термодинамических процессов в Ts-диаграмме
- 14. Изотерма и адиабата в Ts-диаграмме Так
- 15. Ts - диаграмма политропных процессовT0 sn=0p=сonstn=-∞v=сonstn=1T=сonstn=kpvk=сonstn=+∞v=сonstΔu>0Δu
- 16. Основные определения Равновесное состояние, при
- 17. Обратимые и необратимые процессы Все реальные
- 18. II закон термодинамики То есть в I
- 19. Формулировки II закона термодинамики● Карно: для преобразования
- 20. Круговые процессы или циклы Цикл – это
- 21. Обратный цикл В процессе сжатия 261 работа
- 22. Прямой цикл В процессе сжатия 271 работа газа: (lсж=пл.271542)
- 23. Цикл теплового двигателя Запишем для цикла 12341
- 24. Обратимые и необратимые циклы Цикл называется обратимым,
- 25. Цикл Карно1 2 34q1q2p0 v 0
- 26. Процессы, составляющие цикл Карно 1-2 изотермический подвод
- 27. Термический КПД цикла Карно Адиабатный процесс
- 28. Независимость ηt цикла Карно от физических
- 29. Обратный цикл Карно Обратный
- 30. Холодильный коэффициент По I закону термодинамики для
- 31. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Исследование политропных процессов
1. Уравнение процесса выводится из аналитического
выражения I закона термодинамики:
dq=du+pdv; cdT=cvdT+pdv; (c-cv)dT-pdv=0. (1)
Сделаем подстановку
из уравнения Клапейронаpv=RT; T=pv/R; dT=(pdv+vdp)/R.
После подстановки dT в (1) имеем:
(c-cv)(pdv+vdp)/R-pdv=0.
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
Слайд 3Преобразование выражения
I закона термодинамики
Умножим полученное выражение на R/(c-cv):
pdv+vdp-Rpdv/(c-cv)=0.
С учетом уравнения Майера R=cp-cv:
pdv+vdp-(cp-cv)pdv/(c-cv)=0.
После приведения подобных членов и
сокращения имеем:[1-(cp-cv)/(c-cv)]pdv+vdp=npdv+vdp=0.
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
Слайд 4Уравнение политропных процессов
Разделим переменные, поделив уравнение на pv:
ndv/v+dp/p=0.
После интегрирования при n=сonst:
nlnv+lnp=сonst;
или:
ln(pvn)=ln(сonst).После потенцирования получаем уравнение политропных
процессов:
pvn=сonst.
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
Слайд 5Соотношения между параметрами
На предыдущем слайде за показатель политропы
принято
выражение:
n =[1-(cp-cv)/(c-cv)]= (c-cp)/(c-cv).
2. pv-диаграмму политропных процессов рассмотрим
позже.3. Поскольку уравнение политропы pvn=сonst аналогично
уравнению адиабаты pvk=сonst, то все соотношения
между параметрами будут аналогичные:
p1v1n=p2v2n; T2/T1=(v1/v2)n-1; T2/T1=(p2/p1)(n-1)/n.
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
Слайд 6Работа и теплота
4. Изменение внутренней энергии: Δu=cvΔT.
5. Выражения для
работы также запишутся по аналогии с
адиабатным процессом:
l=(p1v1-p2v2)/(n-1); l=(T1-T2)R/(n-1).
6. Теплота по I закону термодинамики:
q=Δu+l.
и через теплоемкость: q=cΔT.
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
Слайд 7Показатель политропы
и энергетический коэффициент
Политропную теплоемкость можно найти из
выражения
показателя политропы:
n=(c-cp)/(c-cv); nc-ncv=c-cp;
приводим подобные члены, умножая и
деля выражение на cv и учитывая, что cp/cv=k:
c=(ncv-cp)cv/(n-1)cv=(n-k)cv/(n-1).
7. Энергетический коэффициент:
φ=Δu/q=cvΔT/[(n-k)cvΔT/(n-1)];
или: φ=(n-1)/(n-k).
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
Слайд 8Обобщающее значение
политропных процессов
Уравнение политропных процессов pvn=сonst справедливо
для любого из частных термодинамических процессов:
● изохорный n=∞: p1/nv=p1/∞v=p0v=v=сonst;
● изобарный n=0: pv0=p=сonst;
● изотермический n=1: pv=const или T=сonst;
● адиабатный n=k: pvk=сonst.
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
Слайд 9Три группы
политропных процессов
На следующем слайде изображены все возможные
термодинамические
процессы.
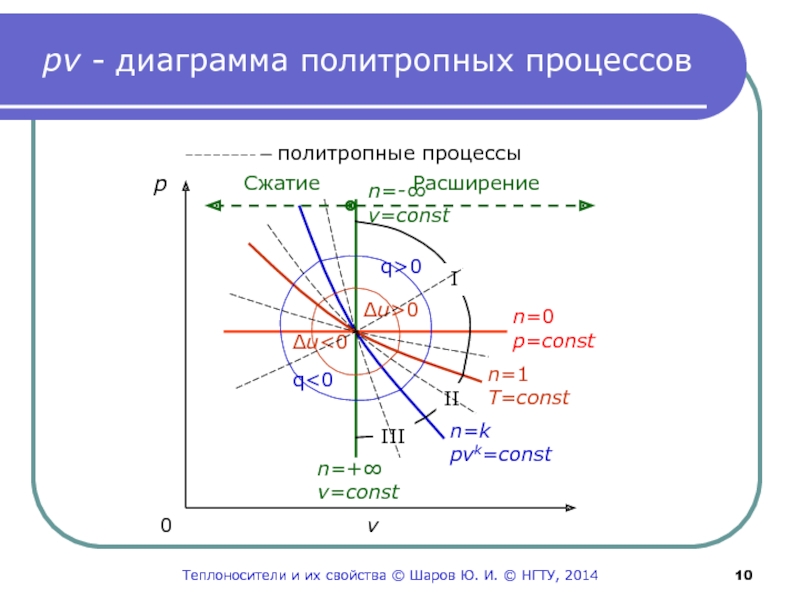
Изотерма T=сonst разделяет их на две группы:
Δu>0 и
Δu<0.Адиабата также делит их на две группы:
q>0 и q<0.
Таким образом, по знакам изменения внутренней энергии и
теплоты процессы расширения газа делятся на I, II и III
группы.
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
Слайд 10pv - диаграмма политропных процессов
p
n=-∞
v=сonst
n=0
p=сonst
n=1
T=сonst
n=k
pvk=сonst
n=+∞
v=сonst
Δu>0
Δu0
q
Расширение
Теплоносители и их свойства © Шаров Ю. И. ©
НГТУ, 2014Слайд 11Энтропия идеального газа
Обозначим через дифференциал энтропии выражение
ds=dq/T, Дж/(кг·К). (1)
Тогда теплоту можно определить как dq=Tds, то есть
площадь
под процессом в Ts-диаграмме.Найдем зависимости T=f(s) для термодинамических
процессов подстановкой в (1) I закона термодинамики:
; (2)
. (3)
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
Слайд 12Изменение энтропии
в термодинамических процессах
Проинтегрировав выражения (2) и
(3), получим изменения
энтропии в политропных процессах:
; (4)
. (5)Из (4) при v=сonst и из (5) при p=сonst получим
изменения энтропии в изохорном и изобарном процессах:
; (6) . (7)
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
Слайд 13 Изображение термодинамических
процессов в Ts-диаграмме
Из выражений (6,
7) следует, что изохора и изобара в Ts-
диаграмме представляют
собой логарифмические кривые.Причем изохора проходит круче изобары, так как
при ΔT=idem:
Δsp>Δsv из-за cp>cv.
Изотерма в Ts-диаграмме отображается горизонтальной
прямой.
Изображение адиабаты вытекает из анализа выражения
dq=0=Tds.
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
Слайд 14Изотерма и адиабата в Ts-диаграмме
Так как T≠0, то
ds=0, следовательно s=сonst – это и
есть уравнение адиабаты в
Ts-диаграмме.На следующем слайде представлена Ts-диаграмма
термодинамических процессов.
Площадь под процессом в Ts-диаграмме представляет
собой теплоту, поэтому она называется тепловой диаграммой.
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
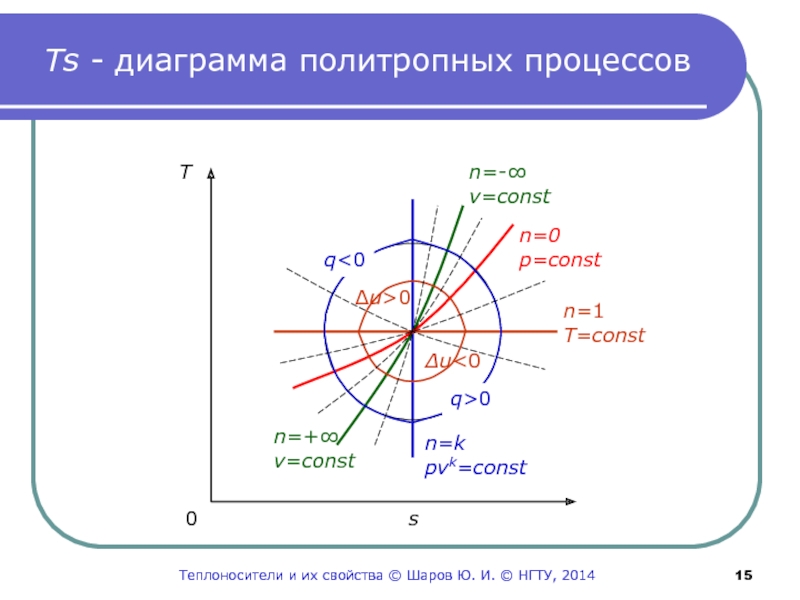
Слайд 15Ts - диаграмма политропных процессов
T
0 s
n=0
p=сonst
n=-∞
v=сonst
n=1
T=сonst
n=k
pvk=сonst
n=+∞
v=сonst
Δu>0
Δu
и их свойства © Шаров Ю. И. © НГТУ, 2014
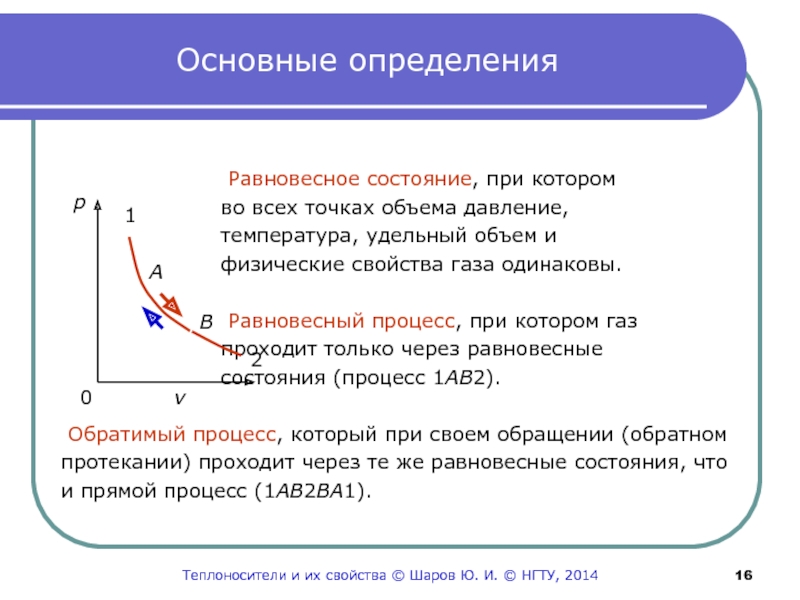
Слайд 16Основные определения
Равновесное состояние, при котором
во всех
точках объема давление,
температура, удельный объем и
физические свойства газа
одинаковы.Равновесный процесс, при котором газ
проходит только через равновесные
состояния (процесс 1АВ2).
Обратимый процесс, который при своем обращении (обратном
протекании) проходит через те же равновесные состояния, что
и прямой процесс (1АВ2ВА1).
p
0 v
A
B
1
2
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
Слайд 17Обратимые и необратимые процессы
Все реальные состояния газа
и процессы – неравновесные
и необратимые.
Термодинамика изучает в первую
очередь обратимые процессы.
Необратимость учитывается эмпирическими
коэффициентами.
По первому закону термодинамики: если к газу подвести
теплоту, то она пойдет на изменение внутренней энергии и
работу против внешних сил.
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
Слайд 18II закон термодинамики
То есть в I законе термодинамики
речь идет о возможности
преобразования тепловой энергии в механическую, но
не приводятся условия его осуществления.
Такое преобразование возможно только в тепловом
двигателе.
Во втором законе термодинамики формулируются условия,
при которых возможно такое преобразование.
Второй закон имеет эмпирический характер. Рассмотрим
несколько формулировок этого закона:
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
Слайд 19Формулировки II закона термодинамики
● Карно: для преобразования тепловой энергии в
механическую необходимы два источника теплоты – горячий
и холодный.
● Томсона:
вся теплота, подведенная от горячего источника к рабочему телу, не может быть преобразована в механическую
энергию; часть этой теплоты должна быть отдана холодному
источнику.
● Планка: невозможно реализовать вечный двигатель II рода.
● Клаузиуса: невозможно передать теплоту от холодного тела
к горячему самопроизвольно, то есть даровым способом.
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
Слайд 20Круговые процессы или циклы
Цикл – это замкнутый процесс, в
конце
которого рабочее тело возвращается в исходное состояние.
При расширении
132 газ совершает работу lp=пл.132451.
Если бы сжатие можно было провести
по той же линии 231, то надо было бы
совершить работу:
lсж=пл.231542=lр;
работа цикла была бы: lц=lр-lсж=0.
p
0 5 4 v
1
2
3
6
7
+
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
Слайд 21Обратный цикл
В процессе сжатия 261 работа газа:
(lсж=пл.261542)>(lp=пл.132451),
следовательно работа такого цикла отрицательная
lц=lр-lсж=пл.13261.
Цикл 13261 совершается
против часовой стрелки и называется обратным, или циклом холодильных установок.
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
Слайд 22Прямой цикл
В процессе сжатия 271 работа газа:
(lсж=пл.271542)
есть работа цикла положительная: lц=lр-lсж=пл.13271.
Цикл 13271 совершается по
часовой стрелке и называется прямым циклом, или циклом теплового двигателя.
Исследования показали, что для получения положительной
работы цикла надо на одном его участке подвести к рабочему
телу теплоту q1 от горячего источника; на другом участке
отвести от рабочего тела теплоту q2 к холодному источнику.
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
Слайд 23Цикл теплового двигателя
Запишем для цикла 12341 I закон
термодинамики
q=q1-q2=l, так как
изменение внутренней энергии для
цикла Δu=u1-u1=0.
Основной характеристикой прямого цикла является его термический КПД –
отношение полезно-использованной
теплоты ко всей подведенной:
.
Так как не может быть q1=∞ или q2=0, то термический КПД
прямого цикла всегда меньше единицы (ηt<1).
q1
1
2
p 3
4
q2
0 v
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
Слайд 24Обратимые и необратимые циклы
Цикл называется обратимым, если он
состоит только из
обратимых процессов. Все реальные процессы необратимые,
поэтому
реальные циклы необратимы.Термодинамика изучает обратимые циклы, необратимость
же учитывается эмпирическими коэффициентами.
Карно предложил оптимальный теоретический цикл для
преобразования теплоты в механическую энергию, который
невозможно осуществить в реальном тепловом двигателе.
Значение цикла Карно заключается в том, что он имеет
максимальный КПД в заданном диапазоне температур.
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
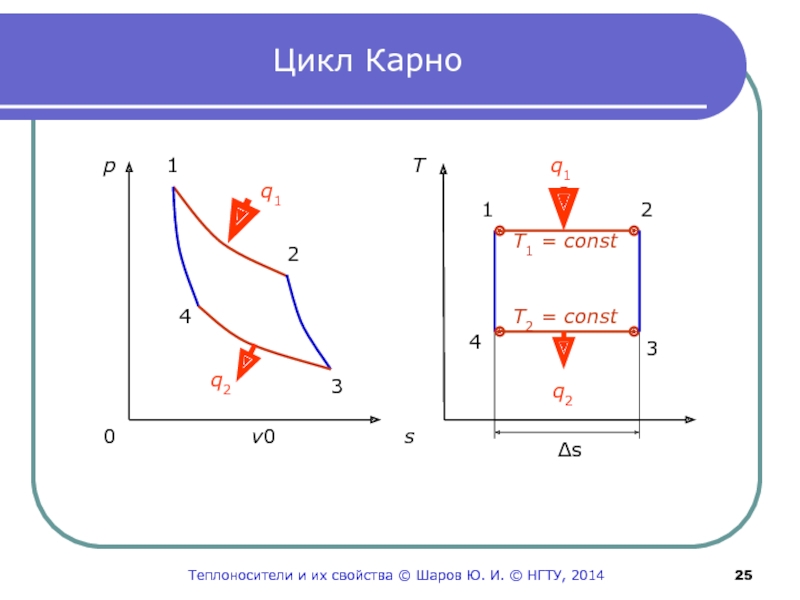
Слайд 25Цикл Карно
1
2
3
4
q1
q2
p
0 v 0 s
T
1
2
3
4
q1
q2
Δs
T1 = сonst
T2 = сonst
Теплоносители и их свойства © Шаров
Ю. И. © НГТУ, 2014Слайд 26Процессы, составляющие цикл Карно
1-2 изотермический подвод теплоты от
энергоемкого
горячего источника к рабочему телу;
2-3 адиабатное расширение
рабочего тела;3-4 изотермический отвод теплоты от рабочего тела к
энергоемкому холодному источнику;
4-1 адиабатное сжатие рабочего тела.
Изотермический процесс самый экономичный для подвода
теплоты, так как в нем, согласно I закону термодинамики,
вся подведенная к газу теплота расходуется только на
работу (q=l).
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
Слайд 27Термический КПД цикла Карно
Адиабатный процесс расширения газа
самый подходящий,
так как в нем нет потерь теплоты от
газа в окружающую среду (q=0).
В Ts-диаграмме (тепловой) площадь под процессом
представляет собой теплоту, поэтому термический КПД
цикла Карно:
.
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
Слайд 28Независимость ηt цикла Карно
от физических свойств рабочего тела
В выражении термического КПД нет физических свойств
рабочего тела.
Значит ηt цикла Карно зависит только от температур
горячего и холодного источников.
Причем, чем шире диапазон температур цикла, тем выше его
термический КПД.
На следующем слайде в Ts-диаграмме изображены в одном
диапазоне температур от T2 до T1 произвольный цикл
ABCDА и описанный вокруг него цикл Карно 12341.
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
Слайд 29Обратный цикл Карно
Обратный цикл Карно характеризует
совершенство передачи теплоты от
холодного источника к горячему.
1-2 адиабатное расширение рабочего
тела;
2-3 изотермический подвод теплоты
от холодного источника к рабочему
телу;
3-4 адиабатное сжатие рабочего тела;
4-1 изотермический отвод теплоты от рабочего тела к
горячему источнику.
T q1
1 4
q2
2 3
0 s
T1=сonst
T2=сonst
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014
Слайд 30Холодильный коэффициент
По I закону термодинамики для цикла:
q=
q1-q2=l.
Основной характеристикой обратного цикла является
холодильный коэффициент:
ε=q2/(q1-q2)=q2/l.
Для обратного цикла Карно:
ε=T2Δs/(T1Δs-T2Δs)=T2/(T1-T2).
Теплоносители и их свойства © Шаров Ю. И. © НГТУ, 2014




![ТНиС 04 Соотношения между параметрами На предыдущем слайде за показатель политропы принято выражение: Соотношения между параметрами На предыдущем слайде за показатель политропы принято выражение: n =[1-(cp-cv)/(c-cv)]= (c-cp)/(c-cv). 2. pv-диаграмму политропных](/img/thumbs/3d17e241bde660392ba445dc3ad435a9-800x.jpg)