Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Трение в кинематических парах и механизмах Часть 2
Содержание
- 1. Трение в кинематических парах и механизмах Часть 2
- 2. Вопросы лекцииТрение в винтовой пареТрение во вращательной кинематической пареТрение качения
- 3. 1.Трение в винтовой паре Допущение: давление гайки
- 4. 2. Трение во вращательной кинематической пареMωrRNFтрМомент тренияRρКруг
- 5. Трение в подпятникеQrRdαdρdsρRrДлина элементарной дугиДлина дугиПлощадь элементарногоучасткаЭлементарная реакцияq-удельное давлениеЭлементарная сила трения
- 6. Трение в подпятникеМомент тренияДля сплошного подпятника
- 7. Трение в гибкой нитиVS1S2SS+dSdNdδαДля равномерного движения необходимо:S2
- 8. Трение в гибкой нитиSS+dSdNФормула ЭйлераF = S2 - S1 = dS
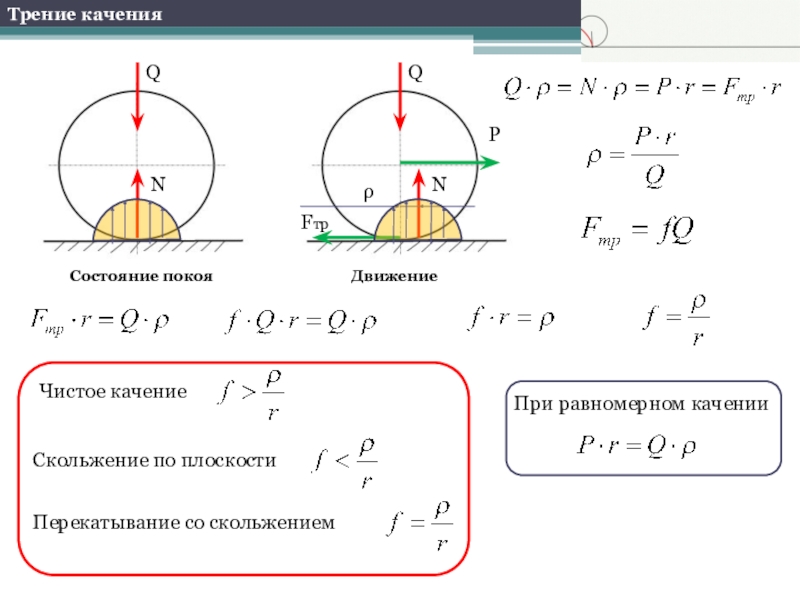
- 9. Трение каченияQNСостояние покояQNρPFтрДвижениеПерекатывание со скольжениемСкольжение по плоскостиЧистое качениеПри равномерном качении
- 10. Конец лекции
- 11. Скачать презентанцию
Вопросы лекцииТрение в винтовой пареТрение во вращательной кинематической пареТрение качения
Слайды и текст этой презентации
Слайд 1Трение в кинематических парах и механизмах
Часть 2
Лекция
НЕСМИЯНОВ Иван Алексеевич
Теория механизмов
и машин
Слайд 31.Трение в винтовой паре
Допущение: давление гайки на винт приложено по
средней линии, т.к. закон распределения давлений по резьбе неизвестен.
Р –
касательная сила
Q – осевая сила
R
α-угол подъема
резьбы
R
у
х
Р
Q
Fтр
N
α
α
φ
Слайд 42. Трение во вращательной кинематической паре
M
ω
r
R
N
Fтр
Момент трения
R
ρ
Круг радиуса ρ называется
кругом трения
При равномерном вращении Мтр уравновешивает
момент приложенный к
валу (Мтр=Мдв);Если R проходит внутри окружности трения, то вал
останавливается.
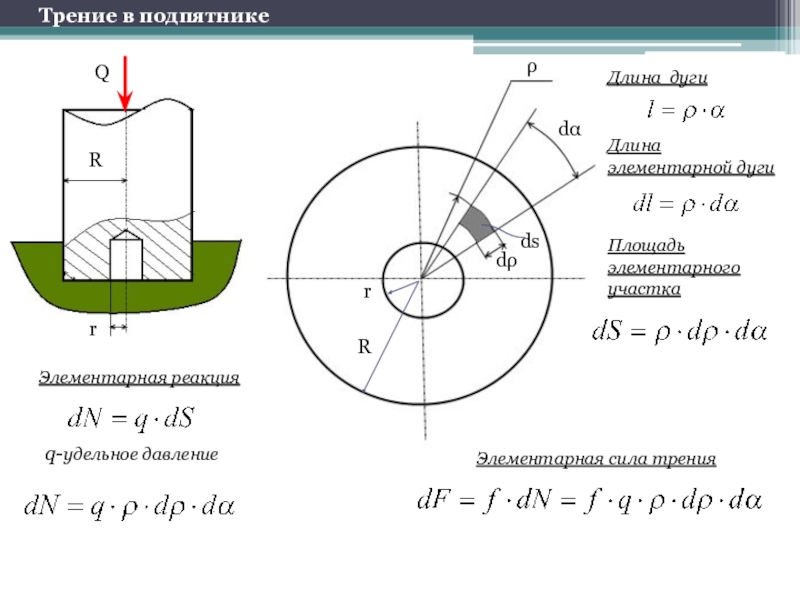
Слайд 5Трение в подпятнике
Q
r
R
dα
dρ
ds
ρ
R
r
Длина
элементарной дуги
Длина дуги
Площадь
элементарного
участка
Элементарная реакция
q-удельное давление
Элементарная сила
трения
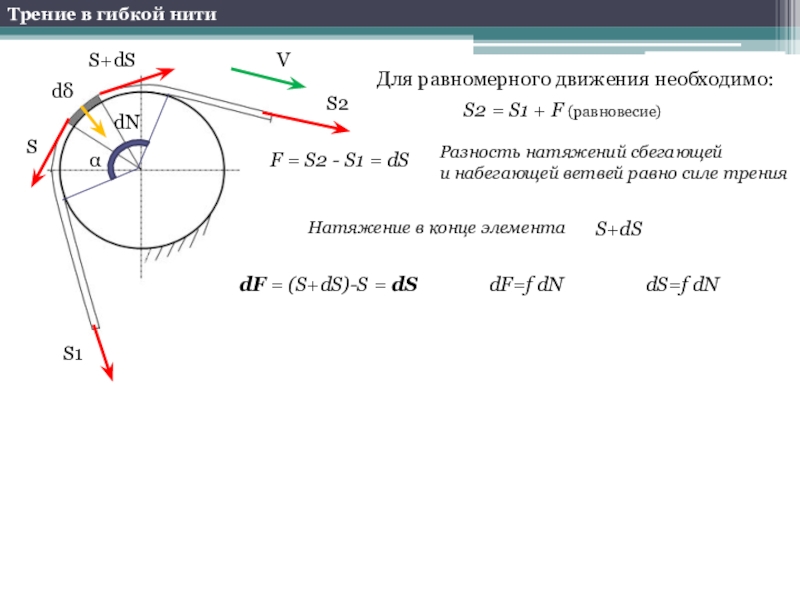
Слайд 7Трение в гибкой нити
V
S1
S2
S
S+dS
dN
dδ
α
Для равномерного движения необходимо:
S2 = S1 +
F (равновесие)
F = S2 - S1 = dS
Разность натяжений сбегающей
и набегающей ветвей равно силе трения
S+dS
Натяжение в конце элемента
dF = (S+dS)-S = dS
dF=f dN
dS=f dN
Слайд 9Трение качения
Q
N
Состояние покоя
Q
N
ρ
P
Fтр
Движение
Перекатывание со скольжением
Скольжение по плоскости
Чистое качение
При равномерном качении
