Творческая работа по теме: П реобразовани я графиков функции

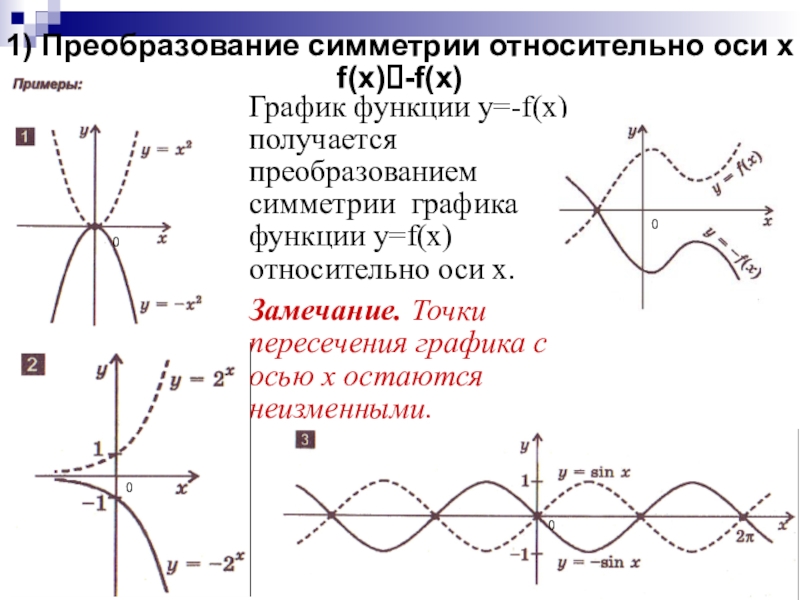
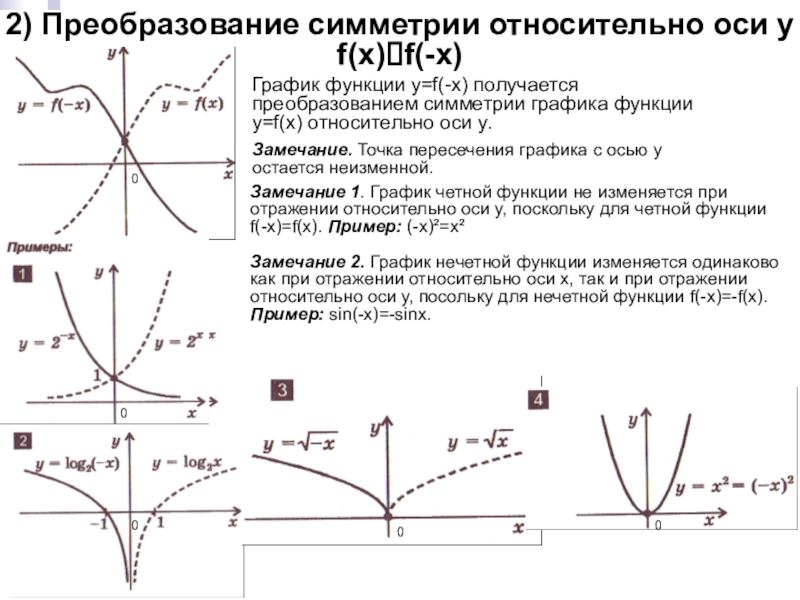
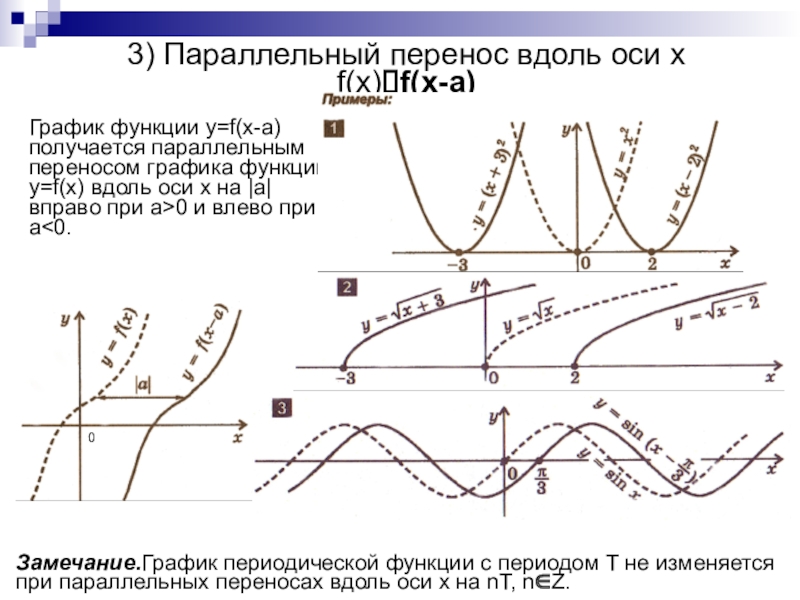
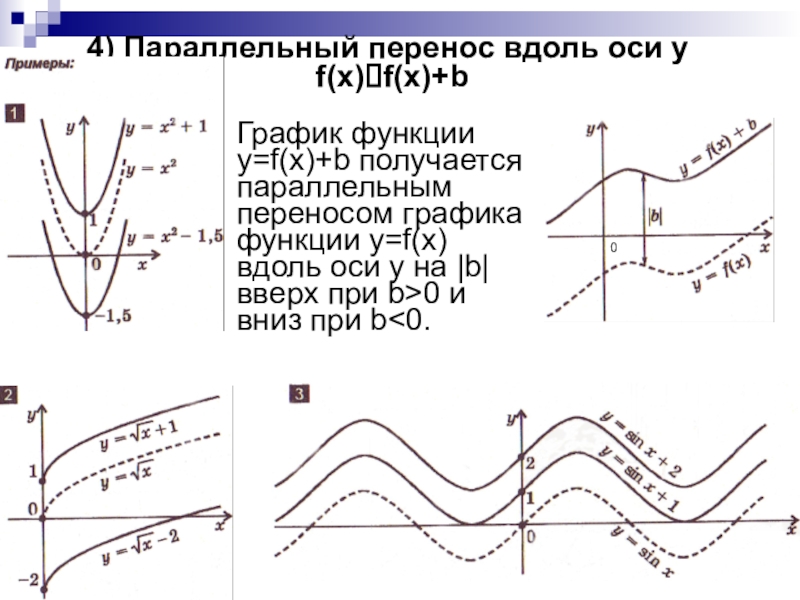
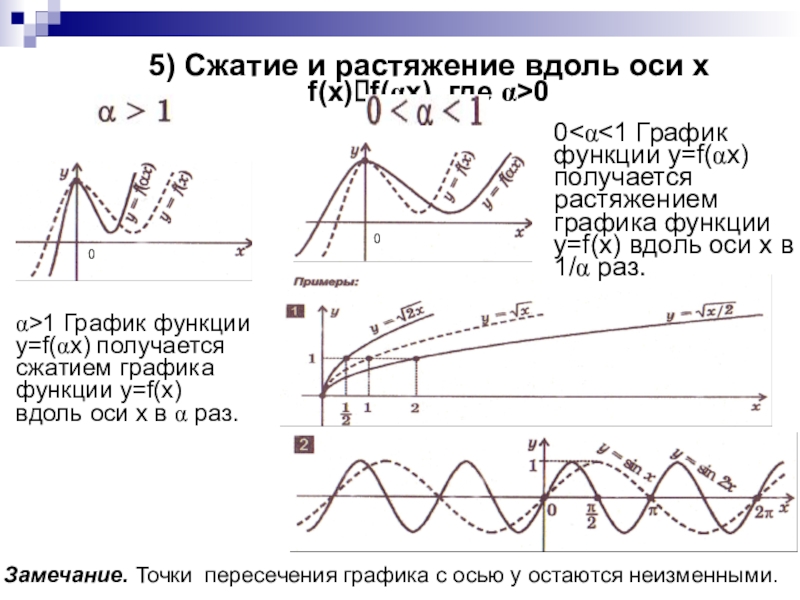
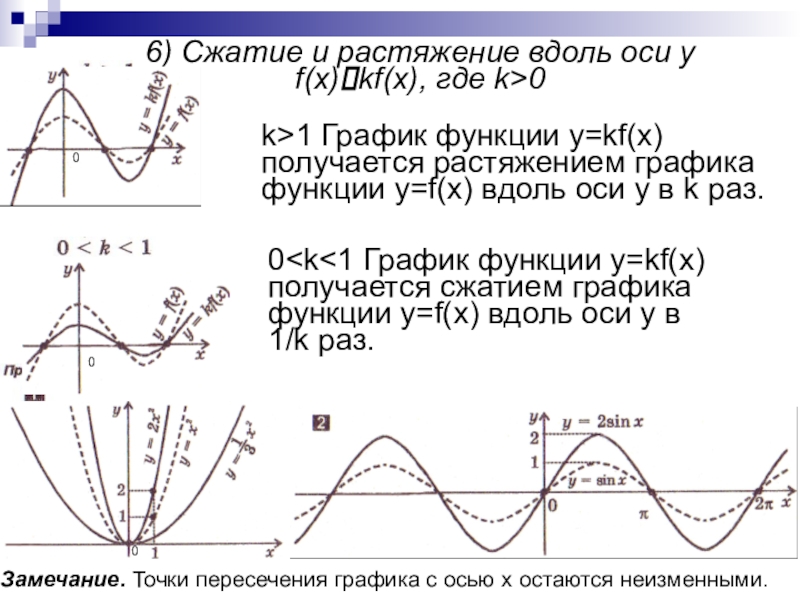
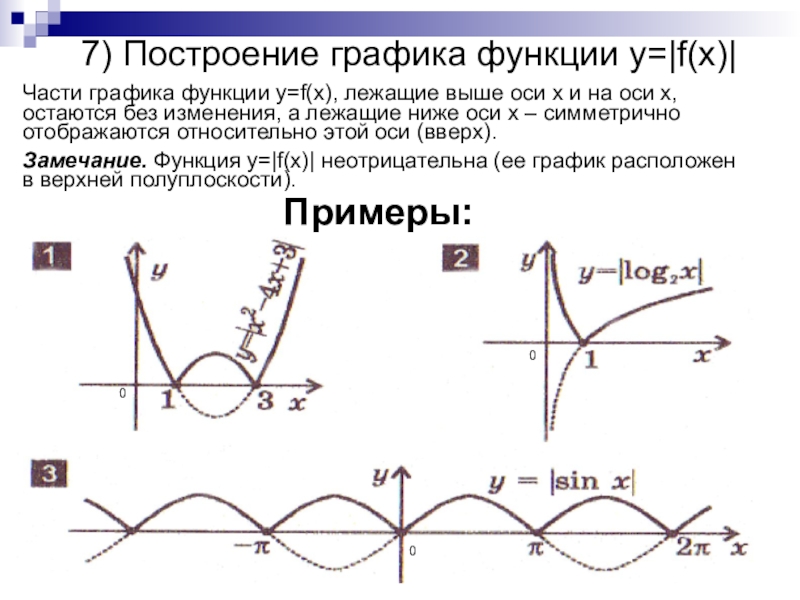
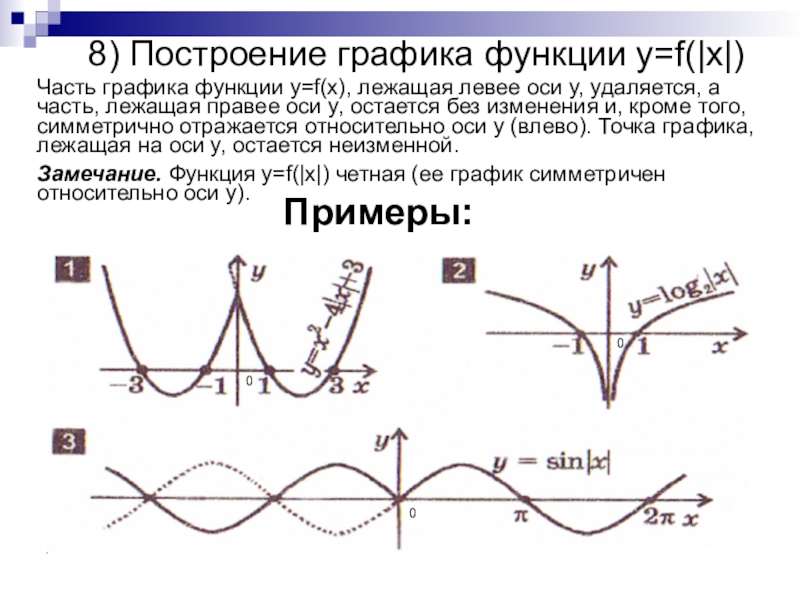
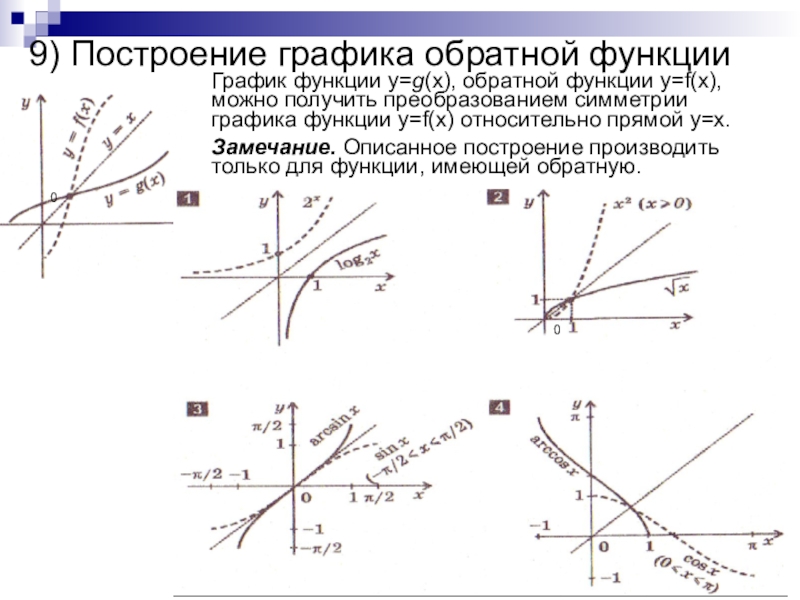
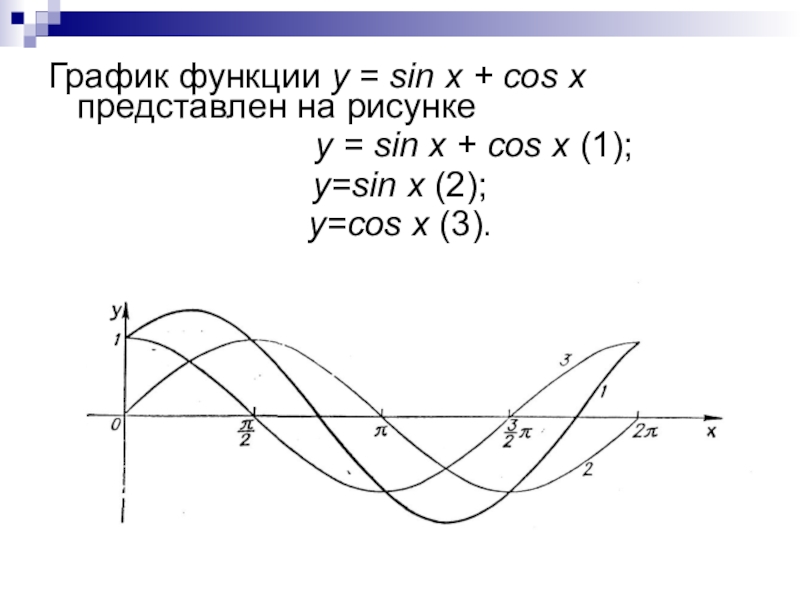
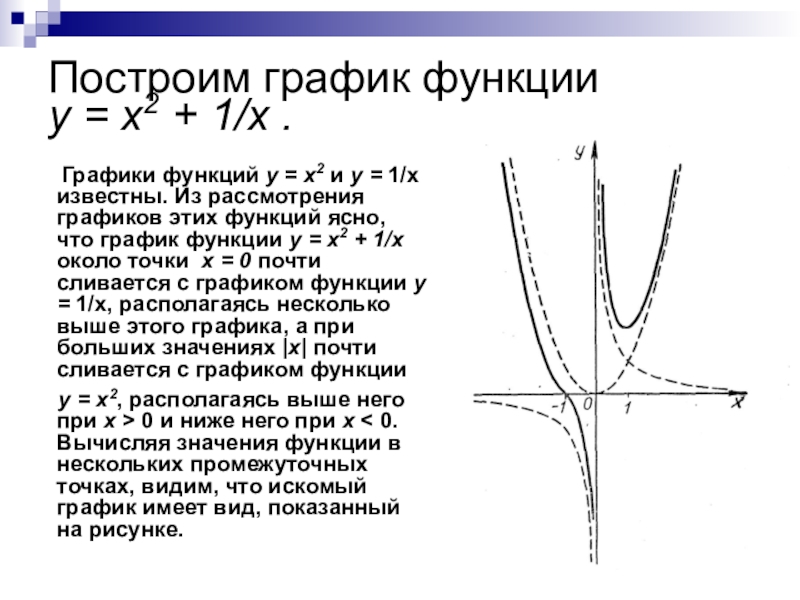
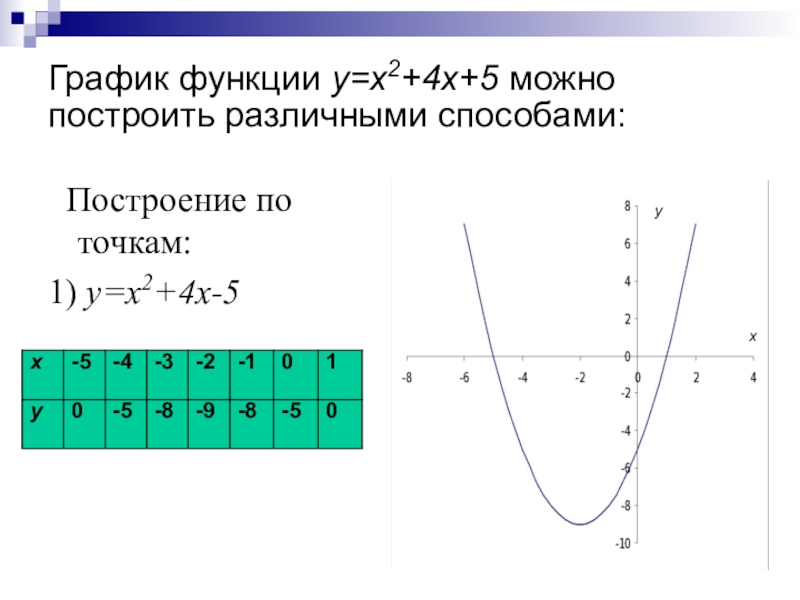
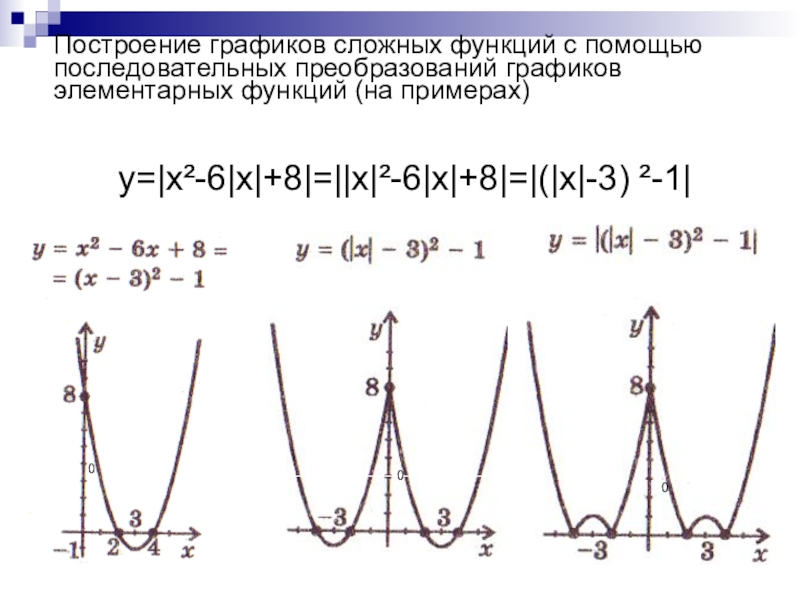
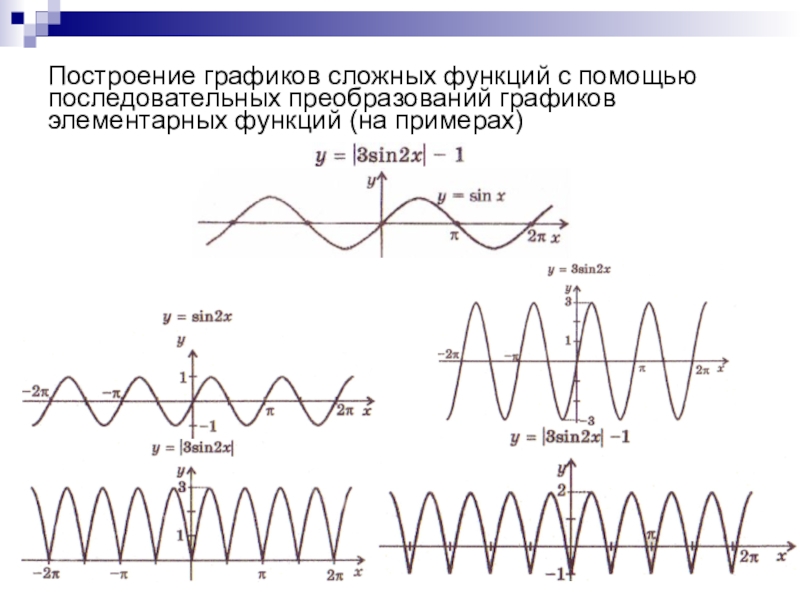
преобразований для построения графиков функции.

Воспитательная: Формирование умения применять геометрические преобразования

при построении:
а) графиков сложных функций;
б) при решении заданий ЕГЭ из части C.

симметрии графика функции y=f(x) относительно оси x.
Замечание. Точки пересечения графика

с осью x остаются неизменными.

симметрии графика функции y=f(x) относительно оси y.
Замечание. Точка пересечения графика

с осью y остается неизменной.

Замечание 1. График четной функции не изменяется при отражении относительно оси y, поскольку для четной функции f(-x)=f(x). Пример: (-x)²=x²

Замечание 2. График нечетной функции изменяется одинаково как при отражении относительно оси x, так и при отражении относительно оси y, посольку для нечетной функции f(-x)=-f(x). Пример: sin(-x)=-sinx.

0

параллельным переносом графика функции y=f(x) вдоль оси x на |a|

вправо при a>0 и влево при a<0.

Замечание.График периодической функции с периодом T не изменяется при параллельных переносах вдоль оси x на nT, nZ.

получается параллельным переносом графика функции y=f(x) вдоль оси y на

|b| вверх при b>0 и вниз при b<0.

функции y=f(x) получается сжатием графика функции y=f(x) вдоль оси x

в  раз.

Замечание. Точки пересечения графика с осью y остаются неизменными.

0<<1 График функции y=f(x) получается растяжением графика функции y=f(x) вдоль оси x в 1/ раз.

функции y=kf(x) получается растяжением графика функции y=f(x) вдоль оси y

в k раз.

0

Замечание. Точки пересечения графика с осью x остаются неизменными.

оси x и на оси x, остаются без изменения, а

лежащие ниже оси x – симметрично отображаются относительно этой оси (вверх).
Замечание. Функция y=|f(x)| неотрицательна (ее график расположен в верхней полуплоскости).

Примеры:

0

0

0

оси y, удаляется, а часть, лежащая правее оси y, остается

без изменения и, кроме того, симметрично отражается относительно оси y (влево). Точка графика, лежащая на оси y, остается неизменной.
Замечание. Функция y=f(|x|) четная (ее график симметричен относительно оси y).

Примеры:

0

0

0

можно получить преобразованием симметрии графика функции y=f(x) относительно прямой y=x.
Замечание.

Описанное построение производить только для функции, имеющей обратную.

0

0

двух функций заключается в том, что предварительно строят два графика

для обеих функций, а затем складывают ординаты этих кривых при одних и тех же значениях х (удобно - в характерных точках). По полученным точкам строят искомый график и выполняют проверку в нескольких контрольных точках.

представлен на рисунке

у = sin x + cos x (1);
y=sin x (2);
y=cos x (3).

Графики функций у = х2 и у = 1/х

известны. Из рассмотрения графиков этих функций ясно, что график функции y = x2 + 1/х около точки х = 0 почти сливается с графиком функции у = 1/х, располагаясь несколько выше этого графика, а при больших значениях |x| почти сливается с графиком функции
у = х2, располагаясь выше него при х > 0 и ниже него при х < 0. Вычисляя значения функции в нескольких промежуточных точках, видим, что искомый график имеет вид, показанный на рисунке.

точкам:
1) y=x2+4x-5
у
х

y= x2+4x-5, выделив полный квадрат, получим функцию

у = (x+2)2 - 9. График построим путем сдвига графика функции y=x2 вдоль оси ОХ влево на 2 единицы и вниз на 9 единиц.

х

у

суммы двух функций у=х2 и у=4х-5. Составим таблицу и сложим

соответственные ординаты.

х

у

функций
(на примерах)

функций (на примерах)
y=|x²-6|x|+8|=||x|²-6|x|+8|=|(|x|-3) ²-1|
0
0
0

функций (на примерах)
0
0
0
0

функций (на примерах)

сложных функций.

Помогают найти нетрадиционное решение сложных задач.