Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Упрощение логических схем
Содержание
- 1. Упрощение логических схем
- 2. 1. ГруппировкаПрименение закона ассоциативностиПрименение тождеств – законы отрицанияПример:Возможно использование тождества не относящееся к базовым Пример:
- 3. Теорема о непротиворечивостиПример:Пусть В·С = Х, а D·E = Y, тогдаПрименяя теорему непротиворечивости получаем:
- 4. Приведение выражения к каноническому виду с последующем
- 5. Использование теоремы де МорганаПосле инвертирования правых частейПример:
- 6. Минимизация с помощью карт КарноПравила разметки:Вертикальная ось
- 7. Диаграмма Вейча
- 8. Правила составления контуровКонтуры должны быть прямоугольными и
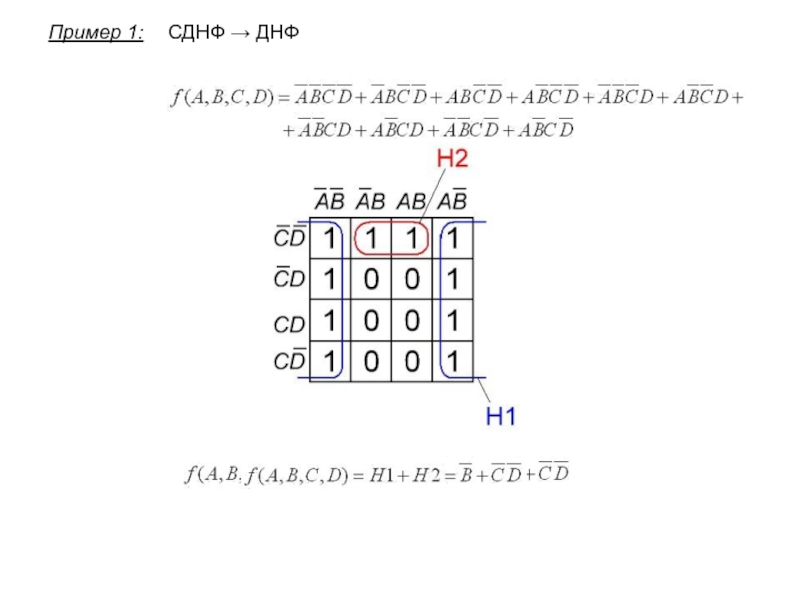
- 9. Пример 1:СДНФ → ДНФ
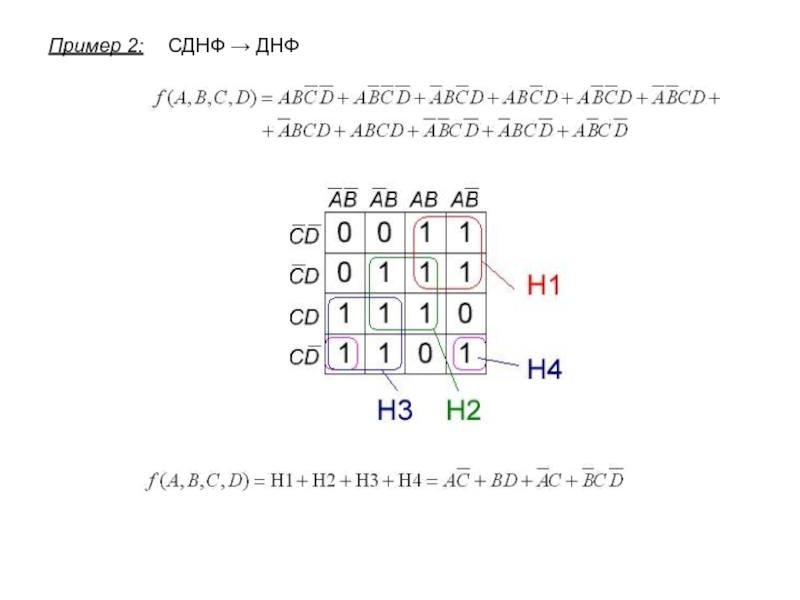
- 10. СДНФ → ДНФПример 2:
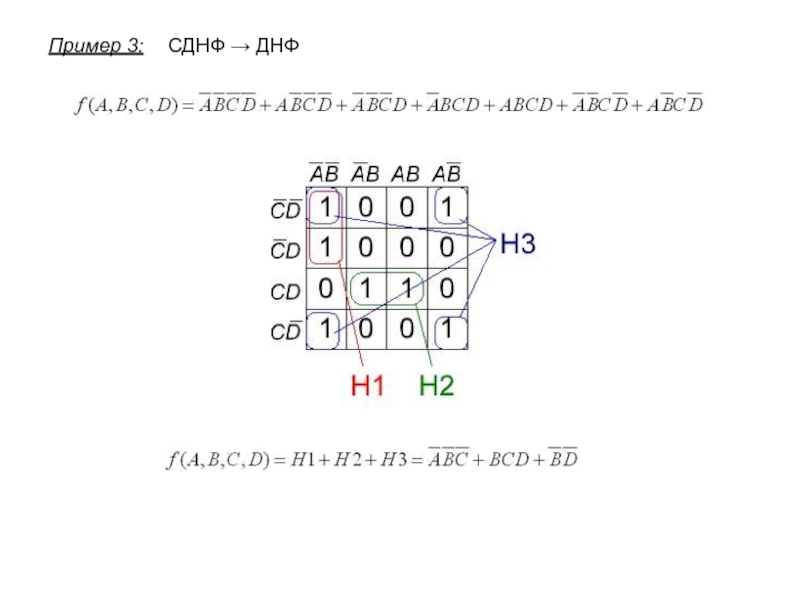
- 11. СДНФ → ДНФПример 3:
- 12. СКНФ → КНФПример 4:
- 13. Построение логических схем
- 14. При построении логических схем следует придерживаться следующей
- 15. Этап IV. Минимизировать СДНФ любым доступным методом.Этап
- 16. Оценка качества функциональных схемВремя задержки распространения сигнала – ТОсновные критерии качества функциональной схемы:Аппаратурные затраты – W
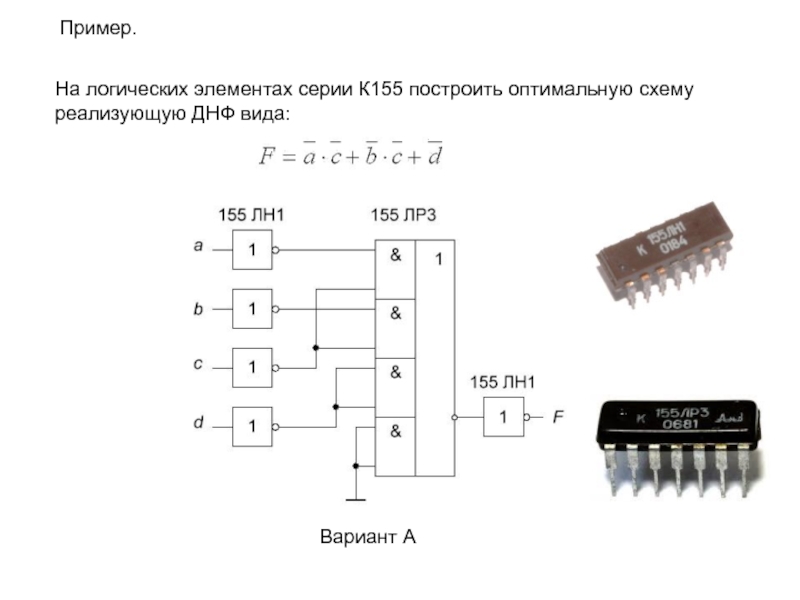
- 17. Пример.На логических элементах серии К155 построить оптимальную схему реализующую ДНФ вида:Вариант А
- 18. T = 3tW = ЛН1 + ЛР3 = 5·1/6 +1 =22/12К155ЛН1
- 19. Рассмотрим другие варианты реализации заданной переключательной функцииПрименив
- 20. Преобразуем выражение так, чтобы уменьшить количество инверторов
- 21. T = 3·tW = 1ЛИ1 + 1ЛЛ1
- 22. Говорят, что х доминирует над х* “по Парето”, если х
- 23. Множество оптимальных “по Парето” решений, то есть
- 24. Соотношение величин задержек Т и аппаратурных затрат
- 25. Скачать презентанцию
1. ГруппировкаПрименение закона ассоциативностиПрименение тождеств – законы отрицанияПример:Возможно использование тождества не относящееся к базовым Пример:
Слайды и текст этой презентации
Слайд 21. Группировка
Применение закона ассоциативности
Применение тождеств – законы отрицания
Пример:
Возможно использование тождества
не относящееся к базовым
Слайд 3Теорема о непротиворечивости
Пример:
Пусть В·С = Х, а D·E = Y,
тогда
Применяя теорему непротиворечивости получаем:
Слайд 4Приведение выражения к каноническому виду с последующем упрощением
1. Выражение записанное
в дизъюнктивной форме можно привести к СДНФ путём умножения импликат
на множитель типа2.После раскрытия скобок, члены выражения могут быть так перегруппированы, что в результате получится упрощенное выражение.
Порядок выполнения операций: сначала выполняются операции конъюнкций, а затем дизъюнкций. В сложных логических выражениях для задания порядка выполнения используют скобки.
При необходимости для формирования групп можно ввести повторяющиеся члены.
Пример:
Слайд 6Минимизация с помощью карт Карно
Правила разметки:
Вертикальная ось размечается независимо от
горизонтальной.
Начинать разметку можно с любого сочетания переменных.
Все сочетания переменных должны
быть перечислены.Для соседних клеток сочетания переменных должны отличаться не более чем одним знаком.
Соседними являются крайние клетки строки или столбца.
Слайд 8Правила составления контуров
Контуры должны быть прямоугольными и содержать количество единиц,
равное 2n, где n – целое число, т.е. в контуре
может быть 1, 2, 4, 8. и т. д. единиц.Количество единиц в контуре должно быть максимальным, при этом контуры могут пересекаться между собой.
Количество контуров должно быть минимальным, но все единицы должны быть охвачены контурами.
Слайд 14При построении логических схем следует придерживаться следующей последовательности:
Этап I. Составление
таблицы истинности производится на основе задания содержащего неформальные признаки (определения,
«хотелки») допускающие неоднозначную трактовку.Основная цель – формализация задания.
Результат этапа – составление задания, неоднозначное толкование которого невозможно, то есть составление полностью и однозначно определённой таблицы истинности.
Этап II. Если функция определена не на всех наборах аргументов, то доопределить функцию нулями или единицами, но так, чтобы уменьшить число членов СДНФ прямой функции или её инверсии.
Этап III. По полностью определённой таблице истинности составить СДНФ или несколько СДНФ в зависимости от количества вариантов доопределения.
Слайд 15Этап IV. Минимизировать СДНФ любым доступным методом.
Этап V. Реализовать получившиеся
дизъюнктивные формы на логическом базисе заданного семейства элементов.
Этап VI. Оценить
двойственный вариант логической схемы с учётом изменения числа входных и выходных инверторов.Этап VII. Попытаться найти такую декомпозицию функции, чтобы каждый фрагмент полученного разложения зависел от возможно меньшего числа аргументов, чем исходная функция. Попытаться выполнить это различными способами.
Этап VIII. Выбрать из полученных на этапах V, VI, VII вариантов наиболее подходящих с точки зрения поставленной задачи
Слайд 16Оценка качества функциональных схем
Время задержки распространения сигнала – Т
Основные критерии
качества функциональной схемы:
Аппаратурные затраты – W
Слайд 17Пример.
На логических элементах серии К155 построить оптимальную схему реализующую ДНФ
вида:
Вариант А
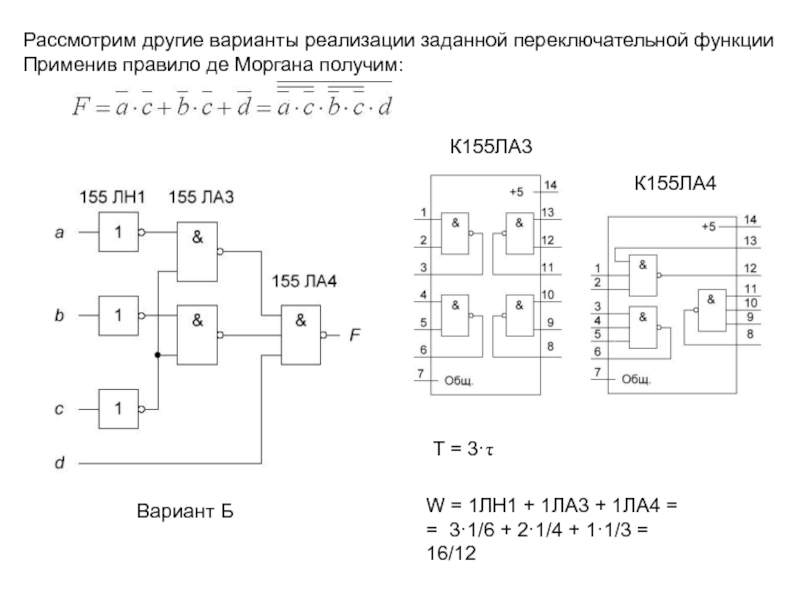
Слайд 19Рассмотрим другие варианты реализации заданной переключательной функции
Применив правило де Моргана
получим:
К155ЛА3
К155ЛА4
Вариант Б
W = 1ЛН1 + 1ЛА3 + 1ЛА4 =
= 3·1/6
+ 2·1/4 + 1·1/3 = 16/12Т = 3·t
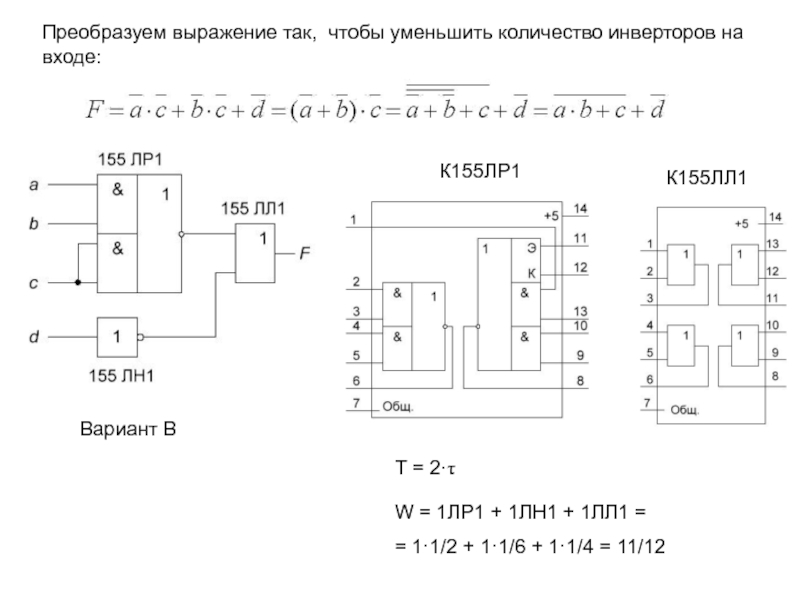
Слайд 20Преобразуем выражение так, чтобы уменьшить количество инверторов на входе:
К155ЛР1
К155ЛЛ1
Вариант В
T
= 2·t
W = 1ЛР1 + 1ЛН1 + 1ЛЛ1 =
=
1·1/2 + 1·1/6 + 1·1/4 = 11/12
Слайд 21T = 3·t
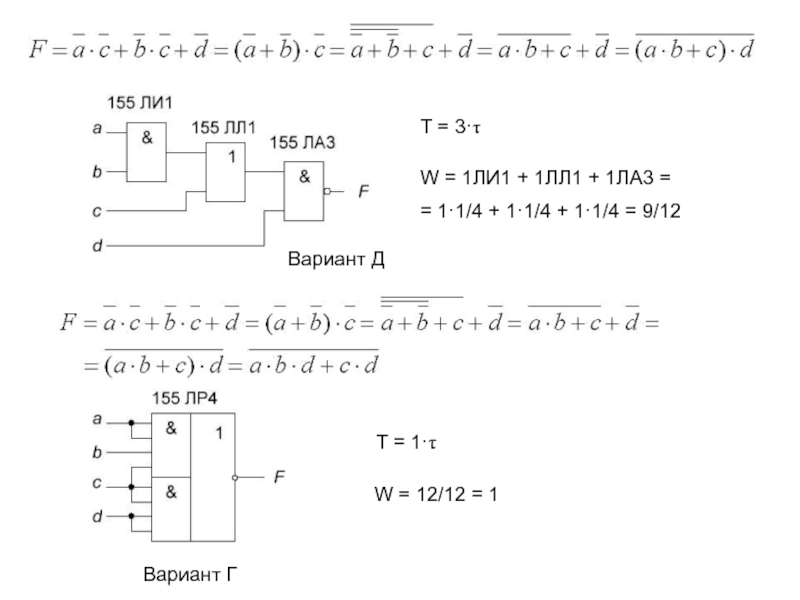
W = 1ЛИ1 + 1ЛЛ1 + 1ЛА3 =
=
1·1/4 + 1·1/4 + 1·1/4 = 9/12
T = 1·t
W =
12/12 = 1Вариант Д
Вариант Г
Слайд 22Говорят, что х доминирует над х* “по Парето”, если х не хуже х*
по всем критериям и хотя бы по одному критерию превосходит
х*. В таком случае в выборе х* нет смысла, так как х по всем параметрам не уступает, а по каким-то и превосходит х.Если рассматривать всего два критерия, то на рисунке 1 показана область пространства, доминируемая решением А. Эта область «замкнута»: элементы на ее границе также доминируемы А.
Рисунок 1 – Доминируемые решения
Решением задачи оптимизации, с несколькими критериями, является множество Парето.
Элемент х* {X} – называется “оптимальным по Парето”, если не существует такого х {X} , который будет “лучше” х*.
Слайд 23Множество оптимальных “по Парето” решений, то есть недоминируемых решений также
называют Парето фронтом.
Рисунок 2 – Парето фронт
Слайд 24Соотношение величин задержек Т и аппаратурных затрат W
W дано в
1/12 долях
• – реальные схемы
х – гипотетические схемы
Множество объектов оптимальных
по Парето.
