Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Уравнение Шредингера
Содержание
- 1. Уравнение Шредингера
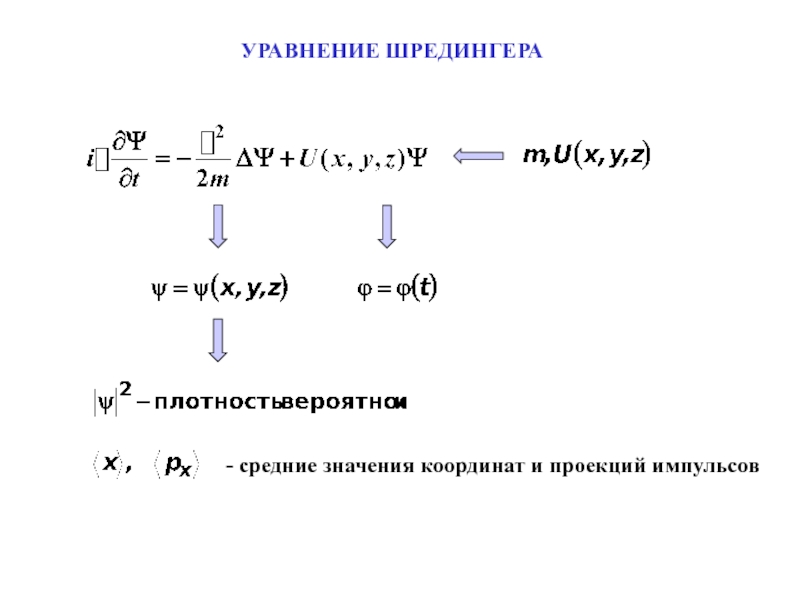
- 2. УРАВНЕНИЕ ШРЕДИНГЕРА
- 3. УРАВНЕНИЕ ШРЕДИНГЕРАУравнение Шредингера для стационарных состояний- потенциальная
- 4. УРАВНЕНИЕ ШРЕДИНГЕРА- средние значения координат и проекций импульсов
- 5. Операторы квантовой механикиОпределение средних значений
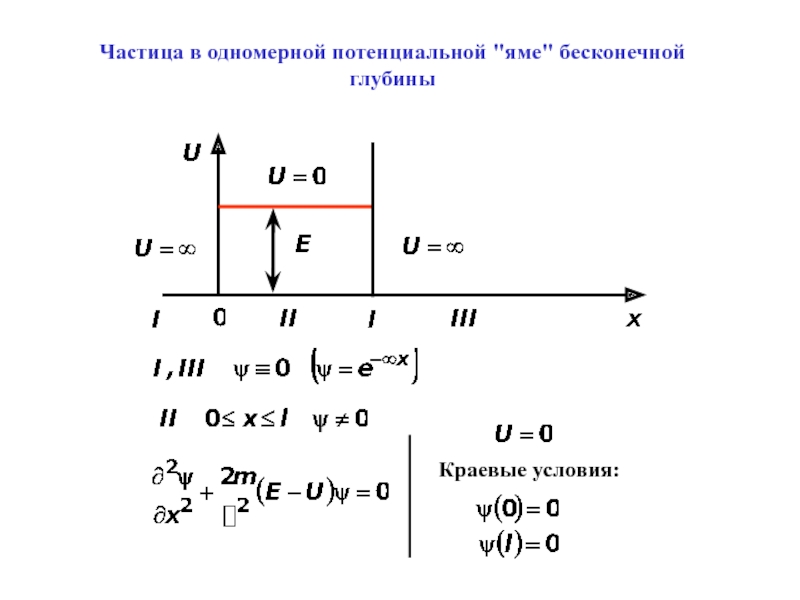
- 6. Частица в одномерной потенциальной "яме" бесконечной глубиныКраевые условия:
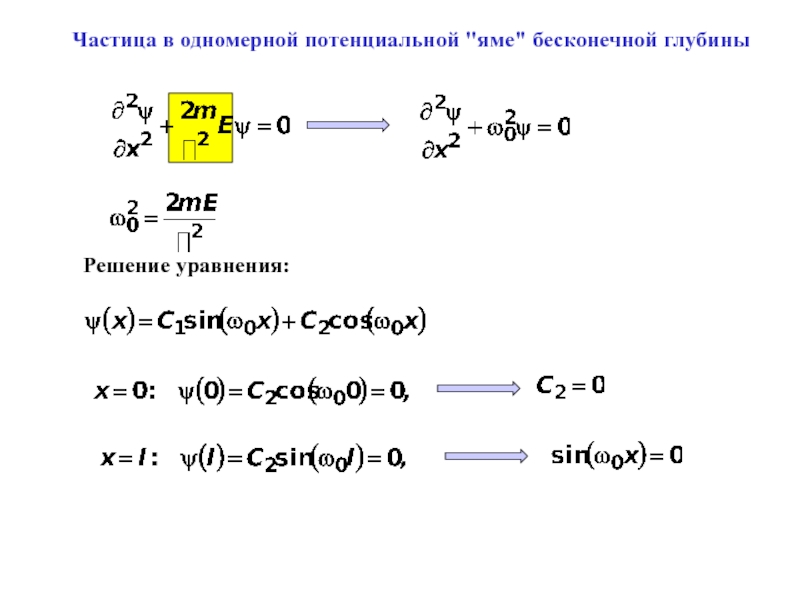
- 7. Частица в одномерной потенциальной "яме" бесконечной глубиныРешение уравнения:
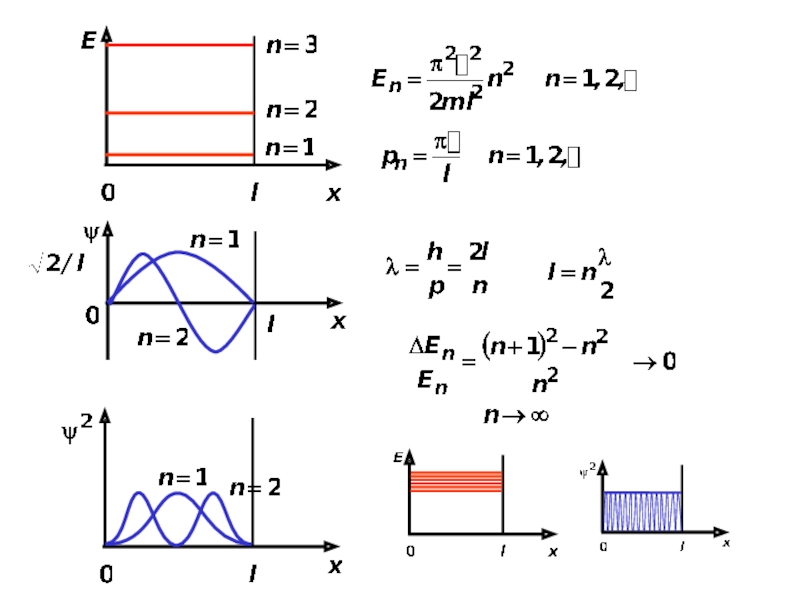
- 8. Частица в одномерной потенциальной "яме" бесконечной глубины- условие квантования энергииn - главное квантовое число
- 9. Слайд 9
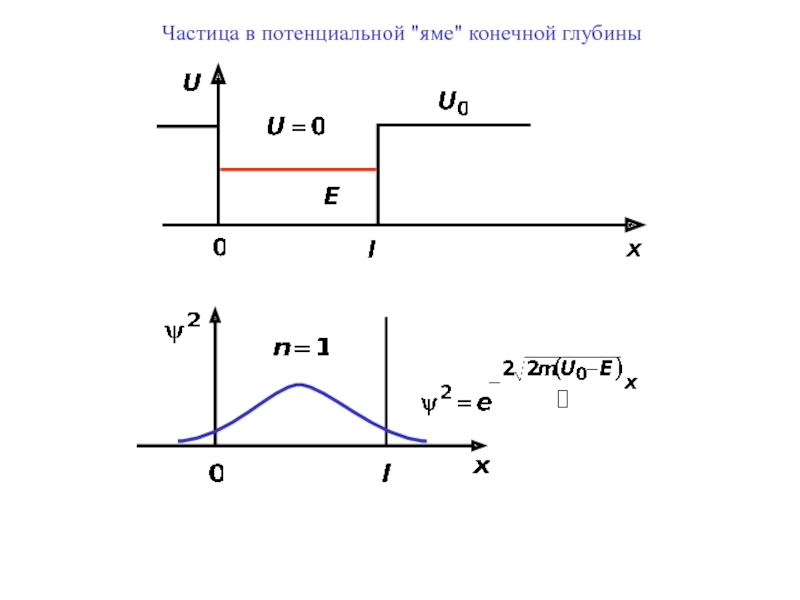
- 10. Частица в потенциальной "яме" конечной глубины
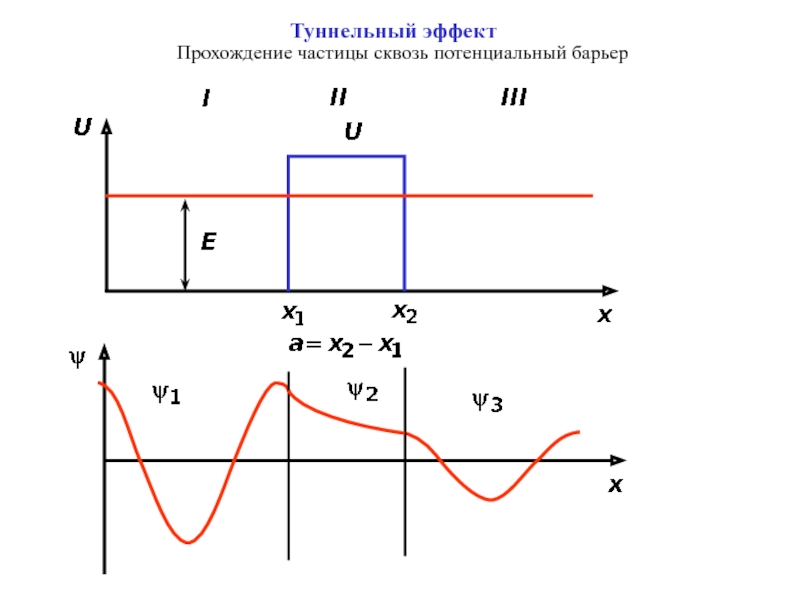
- 11. Туннельный эффектПрохождение частицы сквозь потенциальный барьер
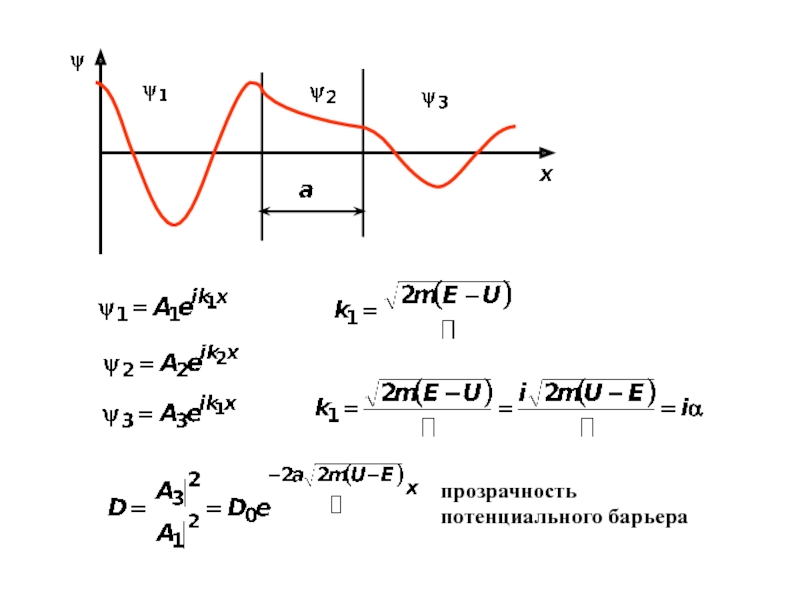
- 12. прозрачность потенциального барьера
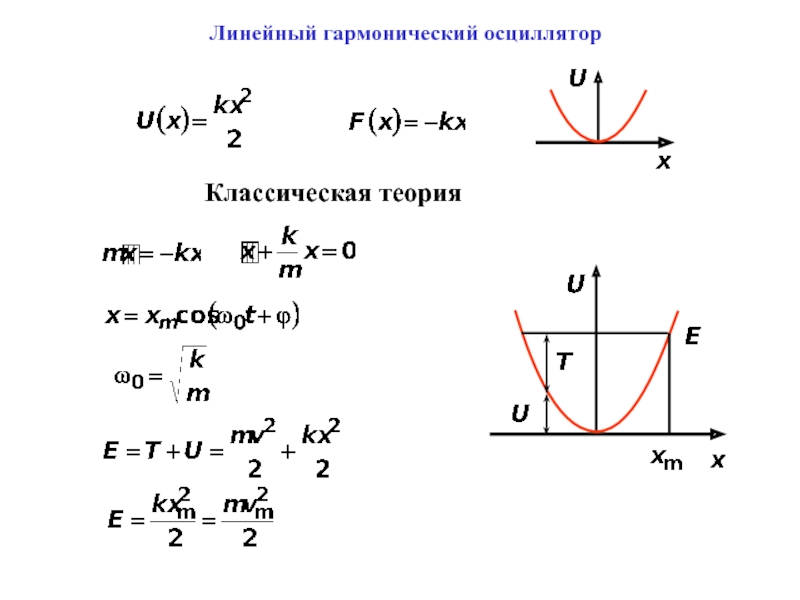
- 13. Линейный гармонический осцилляторКлассическая теория
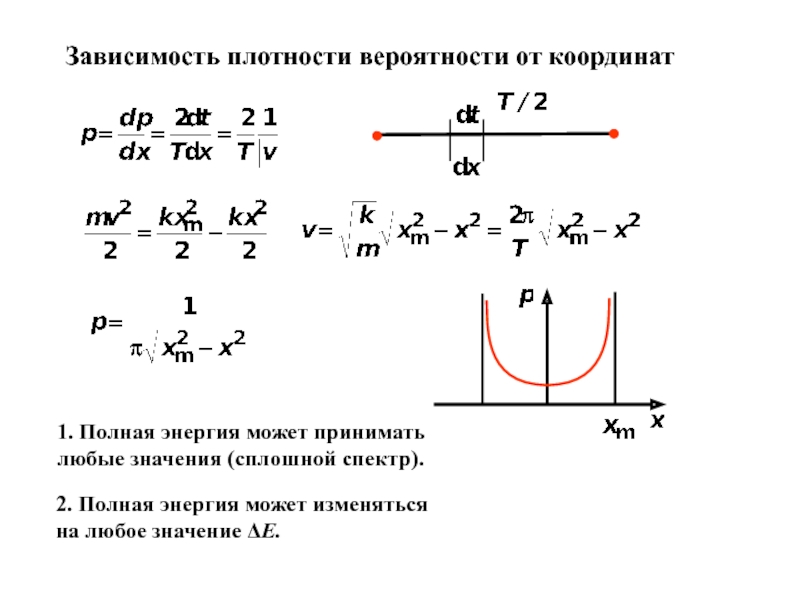
- 14. Зависимость плотности вероятности от координат1. Полная энергия
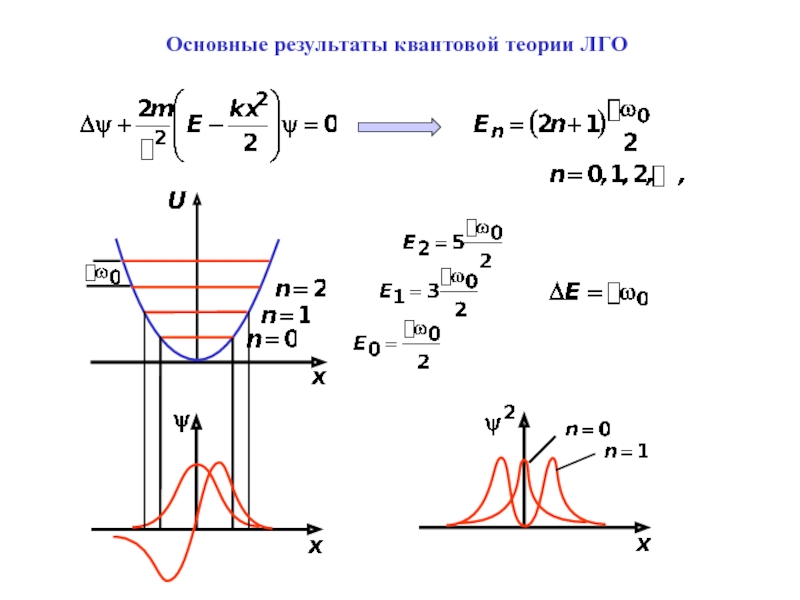
- 15. Основные результаты квантовой теории ЛГО
- 16. Основные результаты квантовой теории ЛГОВыводы:1. Энергия квантового
- 17. Скачать презентанцию
УРАВНЕНИЕ ШРЕДИНГЕРА
Слайды и текст этой презентации
Слайд 1
Уравнение Шредингера для стационарных состояний
Туннельный эффект
Частица в потенциальной яме
Линейный гармонический
осциллятор
Слайд 3УРАВНЕНИЕ ШРЕДИНГЕРА
Уравнение Шредингера для стационарных состояний
- потенциальная энергия частицы в
силовом поле
Особенности решений уравнения Шредингера
Уравнение имеет решения при дискретных значениях
полной энергии E- собственные значения
- собственные функции
Слайд 8
Частица в одномерной потенциальной "яме" бесконечной глубины
- условие квантования энергии
n
- главное квантовое число
Слайд 14Зависимость плотности вероятности от координат
1. Полная энергия может принимать любые
значения (сплошной спектр).
2. Полная энергия может изменяться на любое значение
ΔE.
Слайд 16Основные результаты квантовой теории ЛГО
Выводы:
1. Энергия квантового осциллятора может принимать
дискретные значения
3. Существует минимальное значение энергии осциллятора, отличная от
нуля, - энергия нулевых колебаний
