Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Уравнение окружности Л.С. Атанасян "Геометрия 7-9" Савченко Е.М., учитель
Содержание
- 1. Уравнение окружности Л.С. Атанасян "Геометрия 7-9" Савченко Е.М., учитель
- 2. 1. Как называется геометрическая фигура, состоящая из
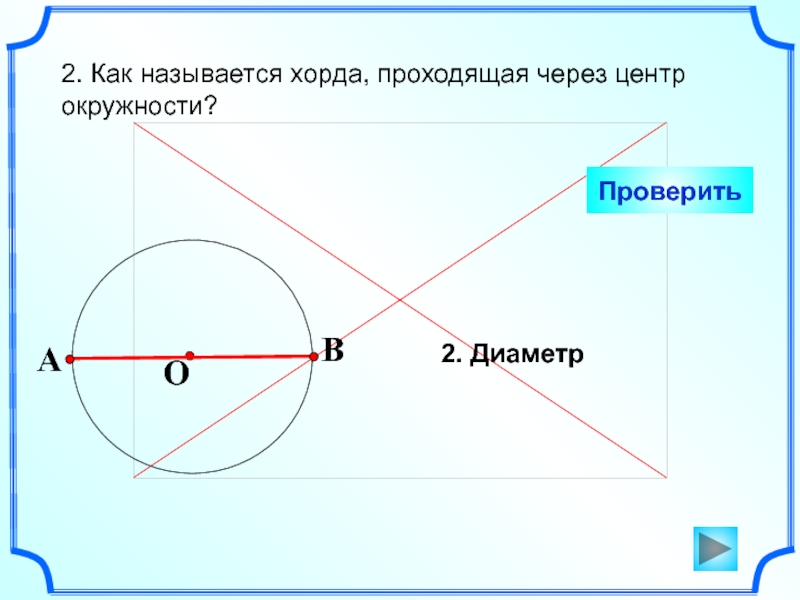
- 3. 2. Как называется хорда, проходящая через центр окружности? Проверить2. Диаметр
- 4. 3. Как называется отрезок, соединяющий центр окружности с точкой на окружности? Проверить3. Радиус
- 5. 4. Как называется геометрическая фигура, состоящая из
- 6. 5. Пересекаются ли окружности с центрами А
- 7. 6. Расстояние от центра окружности до точки
- 8. 7. Расстояние от центра окружности до точки
- 9. (7; 0),
- 10. xyOy = xУравнение линии на плоскости Если
- 11. уравнение окружности
- 12. = 92 (x – )2 +
- 13. ( )= 2 (x –
- 14. (x – 3 )2 + (y –
- 15. (x – 1 )2 + (y –
- 16. (x – 3 )2 + (y –
- 17. (x – 1 )2 + (y –
- 18. ( );(
- 19. Центр?
- 20. (
- 21. Какие из следующих уравнений задают окружность?x2 +
- 22. № 960 (a) Какие из точек
- 23. (x – 1)2 + (y + 3)2
- 24. Дана окружность Определите, какие
- 25. Найдите множество точек, удаленных от окружности
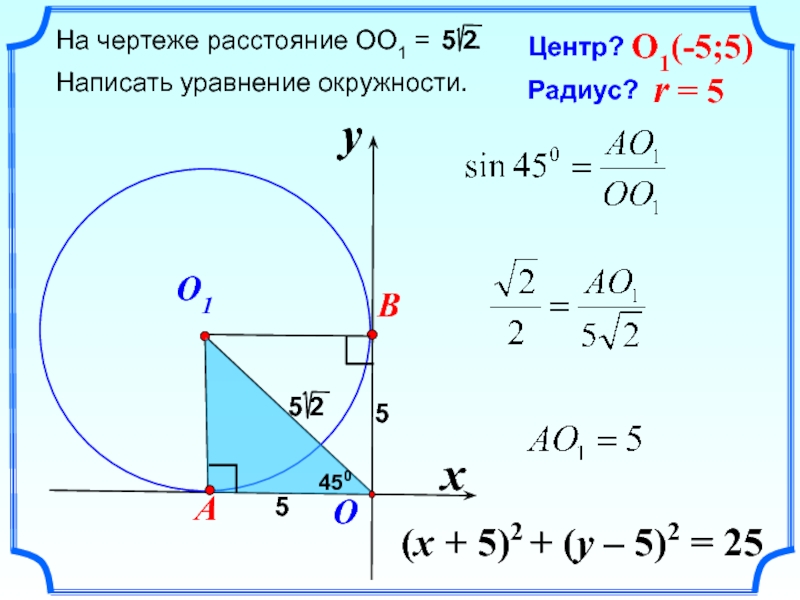
- 26. (x + 5)2 + (y – 5)2 = 25Центр?Радиус?O1(-5;5)r = 5xyAOO145055
- 27. Центр?Радиус?xyO1OE300 На чертеже расстояние ОО1=
- 28. Скачать презентанцию
1. Как называется геометрическая фигура, состоящая из множества всех точек, равноудаленных от данной точки? Математический диктантПроверить1. Окружность
Слайды и текст этой презентации
Слайд 21. Как называется геометрическая фигура, состоящая из множества всех точек,
равноудаленных от данной точки?
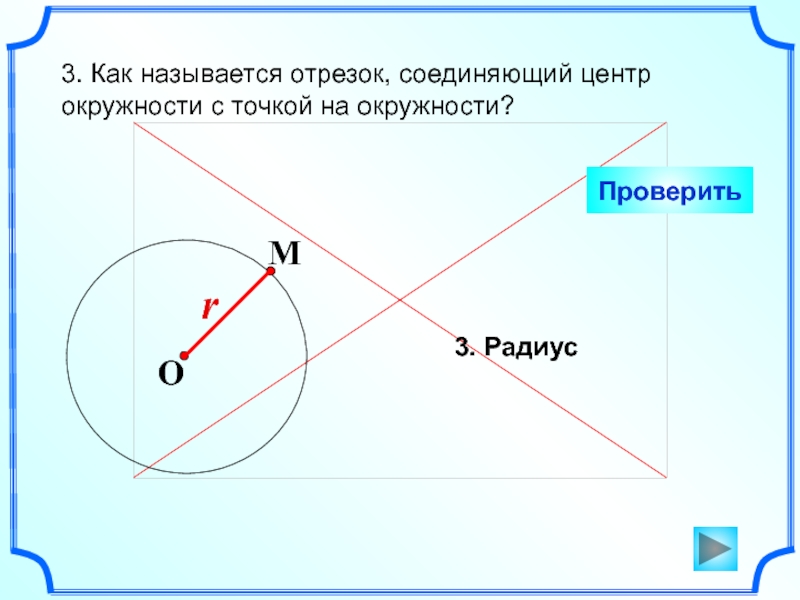
Слайд 43. Как называется отрезок, соединяющий центр окружности с точкой на
окружности?
Проверить
3. Радиус
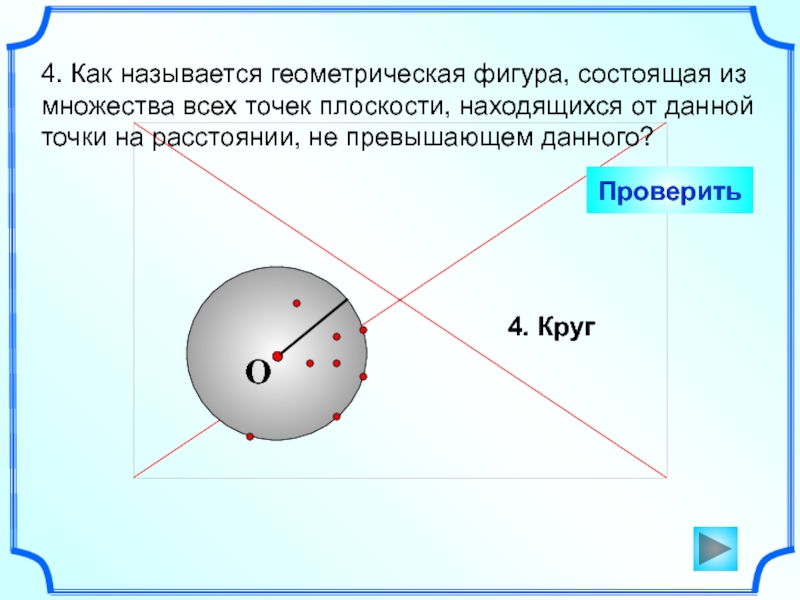
Слайд 54. Как называется геометрическая фигура, состоящая из множества всех точек
плоскости, находящихся от данной точки на расстоянии, не превышающем данного?
Проверить
4. Круг
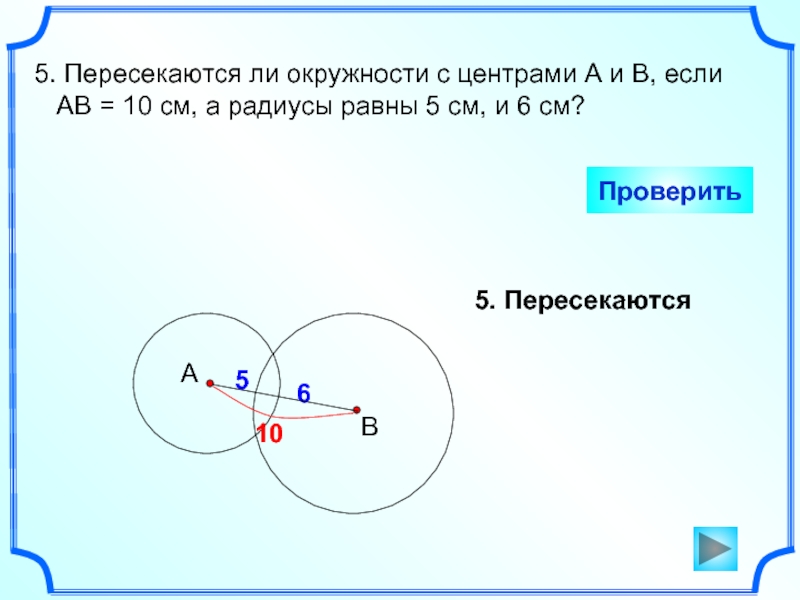
Слайд 65. Пересекаются ли окружности с центрами А и В, если
АВ = 10 см, а радиусы равны 5
см, и 6 см? Проверить
5. Пересекаются
Слайд 76. Расстояние от центра окружности до точки А равно d,
а радиус окружности равен r. Сравните d и r, если
точка Алежит вне круга, ограниченного данной окружностью?
Проверить
6. d > r
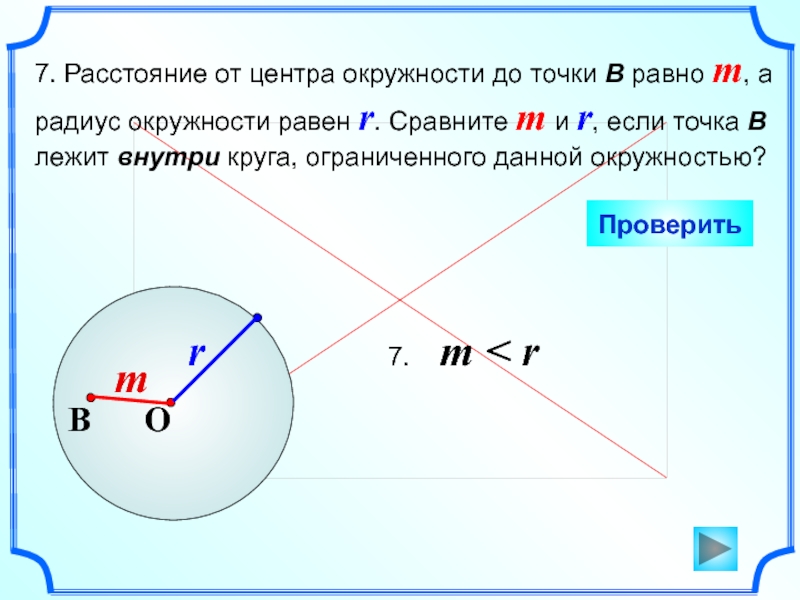
Слайд 87. Расстояние от центра окружности до точки В равно m,
а радиус окружности равен r. Сравните m и r, если
точка B лежит внутри круга, ограниченного данной окружностью?Проверить
7. m < r
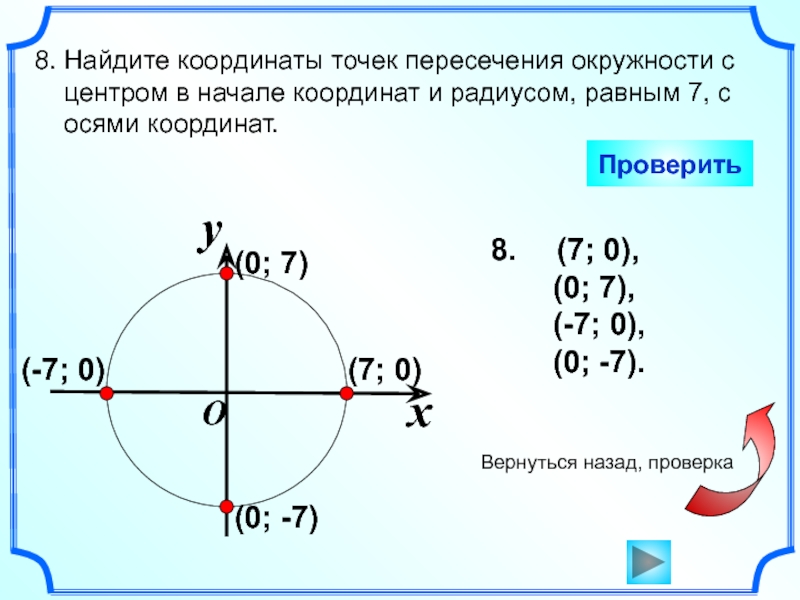
Слайд 9 (7; 0),
(0; 7),
(-7; 0),
(0; -7).
8. Найдите
координаты точек пересечения окружности с центром в начале координат и радиусом, равным 7, с
осями координат.
Проверить
Вернуться назад, проверка
Слайд 10x
y
O
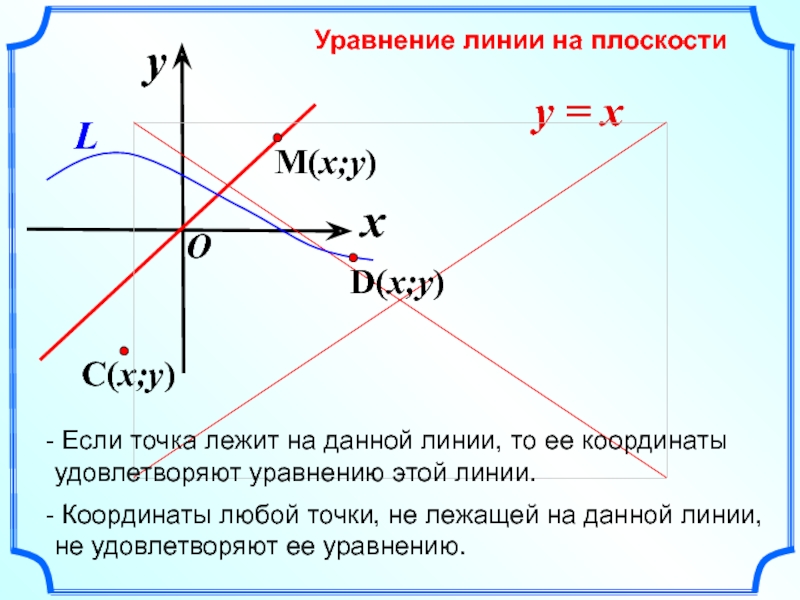
y = x
Уравнение линии на плоскости
Если точка лежит на
данной линии, то ее координаты удовлетворяют уравнению этой линии.
Координаты
любой точки, не лежащей на данной линии, не удовлетворяют ее уравнению.
Слайд 12= 9
2
(x – )2 + (y –
)2
( )
y0
r = 3
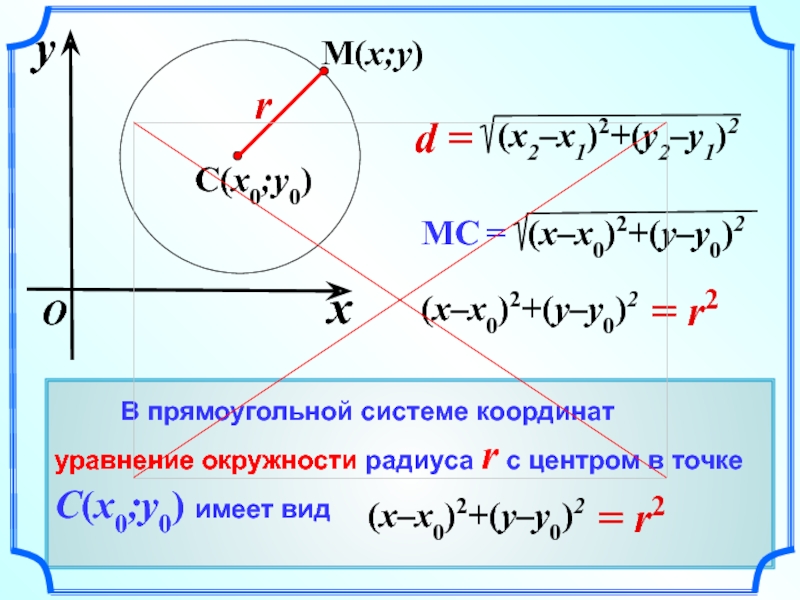
В прямоугольной системе координат уравнение окружности радиуса r с центром в точке C(x0;y0) имеет вид
x
y
O
C(4;-2)
r
= 2
r = 3
3
4
-2
x0
r
Слайд 13( )
= 2
(x – )2 +
(y – )2
C( ; )
= 9
(
) y0
В прямоугольной системе координат
уравнение окружности радиуса r с центром в точке C(x0;y0) имеет вид
x
y
O
r
3
-2
x0
r = 3
-3
y0
x0
C(-3;-2)
Слайд 14(x – 3 )2 + (y – 2)2 = 16
(x
– 1 )2 + (y + 2)2 = 4
(x +
5 )2 + (y – 3)2 = 25(x – 1 )2 + y 2 = 8
x 2 + (y + 2)2 = 2
x 2 + y 2 = 9
(x – 3 )2 + (y – 2)2 = 0,09
(x + 7)2 + (y – 5)2 = 2,5
r
C(3; 2)
C(1;-2)
C(-5; 3)
C(1; 0)
C(0;-2)
C(0; 0)
C(3; 2)
C(-7; 5)
C(0;-4)
r = 4
r = 2
r = 5
r = 3
r = 0,3
Слайд 15(x – 1 )2 + (y – 2)2 = 64
(x
– 1 )2 + (y + 2)2 = 0,64
(x +
5 )2 + y 2 = 1,44x 2 + y 2 = 5
(x + 6)2 + (y + 2)2 = 7
(x – 5)2 + y 2 = 0,0169
(x – 3 )2 + (y + 2)2 = 0,09
(x + 7)2 + (y – 5)2 = 1,6
r
C(1; 2)
r = 8
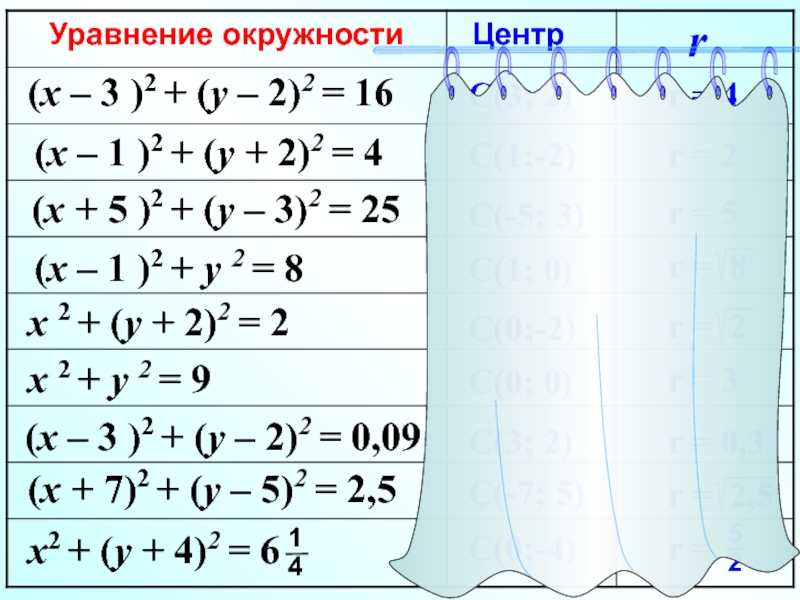
Слайд 16(x – 3 )2 + (y – 2)2 = 16
(x
– 1 )2 + (y + 2)2 = 4
(x +
5 )2 + (y – 3)2 = 25(x – 1 )2 + y 2 = 8
x 2 + (y + 2)2 = 2
x 2 + y 2 = 9
(x – 3 )2 + (y – 2)2 = 0,09
(x + 7)2 + (y – 5)2 = 2,5
r
C(3; 2)
C(1;-2)
C(-5; 3)
C(1; 0)
C(0;-2)
C(0; 0)
C(3; 2)
C(-7; 5)
C(0;-4)
r = 4
r = 2
r = 5
r = 3
r = 0,3
Слайд 17(x – 1 )2 + (y – 2)2 = 64
(x
– 1 )2 + (y + 2)2 = 0,64
(x +
5 )2 + y 2 = 1,44x 2 + y 2 = 5
(x + 6)2 + (y + 2)2 = 7
(x – 5)2 + y 2 = 0,0169
(x – 3 )2 + (y + 2)2 = 0,09
(x + 7)2 + (y – 5)2 = 1,6
r
C(1; 2)
r = 8
Слайд 18( );
( );
(
);
( );
(
);( );
Центр
Вводите ответы в текстовые поля, не делая пробелов
Радиус
(x – 3)2 + (y – 2)2 = 16;
C
r =
r =
r =
r =
r =
r =
C
C
C
C
C
(x + 3)2 + (y – 5)2 = 0,16;
x 2 + (y – 2)2 = 25;
(x – 1)2 + y 2 = 144;
x 2 + y 2 = 2,25;
(x + 7)2 + (y + 1)2 = 0,09;
Слайд 19Центр?
Радиус?
x 2 + y 2 – 6y + 5 =
0;x 2 + y 2 – 6y + 9 – 4 = 0;
( )
x 2 + (y – 3) 2– 4 = 0;
x 2 + (y – 3) 2 = 4
O(0; 3)
r = 2
Слайд 20(
)
Докажите, что линия, заданная уравнением
, является окружностью.
Является ли треугольник АВС вписанным в эту
окружность, если известно, что А(7; -5), В(3;-1), С(-1;-5)?
x 2 – 6x + 9 + y 2 + 10y + 25 – 16 = 0;
( )
(x – 3)2 + (y + 5) 2– 16 = 0;
( x – 3) 2 + ( y + 5) 2 = 16
x2 – 6x + y2 +10y +18 = 0
9
25
16
x2 – 6x + y2 +10y +18 = 0
А(7; -5),
В(3;-1),
С(-1;-5)
7
-5
3
-1
-1
-5
Слайд 21Какие из следующих уравнений задают окружность?
x2 + (y – 1)2
= 25
4x2 + 4y2 = 9
2x2 + 2y2 =
0x2 + y2 + 1 = 0
(x + 2)2 + y2 – 0,01 = 0;
x2 – 2x + y2 = 3;
x2 + y2 = 0
x2 + y2 = – 1
(x + 2)2 + y2 = 0,01
x2 – 2x +1 + y2 = 3 + 1
(x2 –1) + y2 = 4
Слайд 22№ 960 (a) Какие из точек лежат на окружности?
x
2 + y 2 = 25
A(3; -4);
Центр?
Радиус?O(0; 0)
r = 5
B(1; 0);
C(0; 5);
D(0; 0);
E(0; 1);
32 + (-4)2 = 25
12 + 0 2 = 25
02 + 5 2 = 25
0 2 + 0 2 = 25
0 2 + 1 2 = 25
Верно
<
Верно
<
<
y
x
5
Слайд 23(x – 1)2 + (y + 3)2 = 9
№ 960
(б) Какие из точек лежат на окружности?
y
A(3; -4);
Центр?
Радиус?
O(1;-3)
r =
3B(1; 0);
C(0; 5);
D(0; 0);
E(0; 1);
(3 – 1)2 + (– 4 + 3)2 = 9
Верно
<
(1 – 1)2 + (0 + 3)2 = 9
(0 – 1)2 + (5 + 3)2 = 9
>
(0 – 1)2 + (0 + 3)2 = 9
>
(0 – 1)2 + (1 + 3)2 = 9
>
x
Слайд 24 Дана окружность
Определите, какие из точек А(-4;
3), В(5; 1), С(-5; 4), D(10; 5) лежат: а)
на окружности;б) внутри круга, ограниченного данной окружностью;
в) вне круга, ограниченного данной окружностью.
(x – 4 )2 + (y + 3)2 = 100
(– 4 – 4)2 + (3 + 3)2 > 100
(5 – 4)2 + (1 + 3)2 < 100
y
x
(– 5 – 4)2 + (4 + 3)2 > 100
(10 – 4)2 + (5 + 3)2 = 100
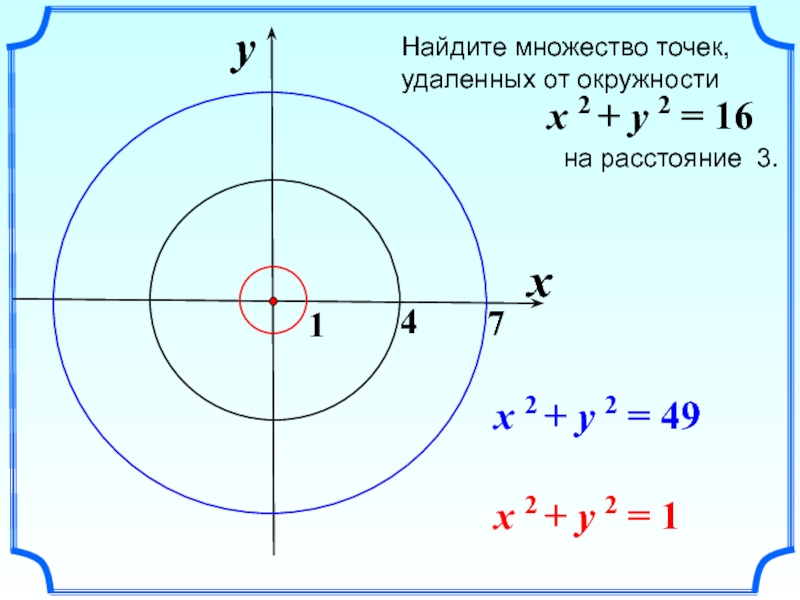
Слайд 25Найдите множество точек, удаленных от окружности
на расстояние 3.
x 2 + y 2 = 16
x
y
x 2 + y 2 = 49
x 2 + y 2 = 1
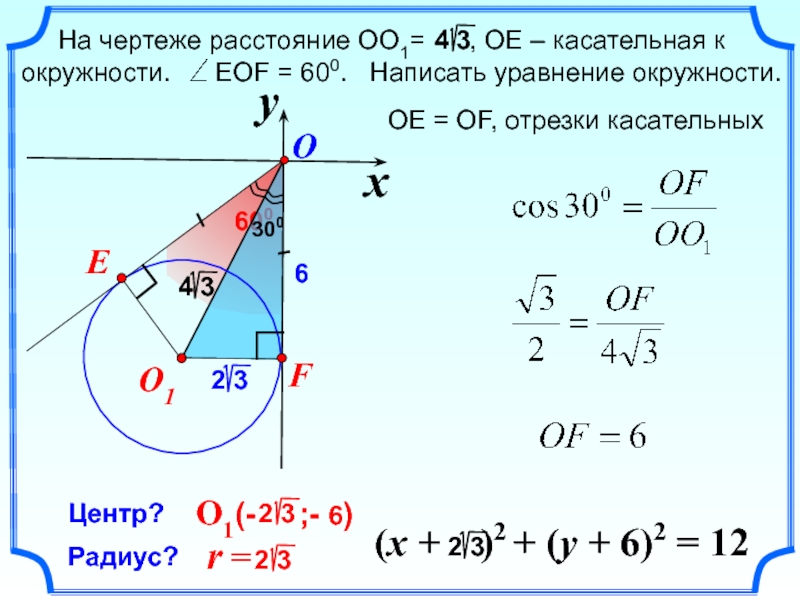
Слайд 27Центр?
Радиус?
x
y
O1
O
E
300
На чертеже расстояние ОО1= ,
ОЕ – касательная к окружности. EOF = 600.
Написать уравнение окружности.ОЕ = ОF, отрезки касательных
6
