Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция 1 Назначение геометрических преобразований
Содержание
- 1. Лекция 1 Назначение геометрических преобразований
- 2. Цель курсаИзучение основных правил и требований к порядку разработки, оформления и обращения конструкторской документации
- 3. Геометрический языкПо С.А. Фролову геометрический язык состоит
- 4. Основные понятия и определенияПлоскостью называется поверхность, образуемая
- 5. Обозначение геометрических фигурГеометрическая фигура обозначается — Ф.2.
- 6. 3. Линии, произвольно расположенные по отношению к
- 7. 4. Поверхности обозначаются строчными буквами греческого алфавита:
- 8. 5. Углы обозначаются: ABC — угол
- 9. 7. Расстояния между геометрическими фигурами обозначаются двумя
- 10. 8. Для плоскостей проекций приняты обозначения:π1, и
- 11. 10. Проекции точек, линий, поверхностей, любой геометрической
- 12. 12. Следы прямых (линий) обозначаются заглавными буквами,
- 13. 11. Следы плоскостей (поверхностей) обозначаются теми же
- 14. 13. Последовательность точек, линий (любой фигуры) отмечается
- 15. Аксонометрические проекции14. Аксонометрические проекции точек, линий, поверхностей
- 16. Вторичные проекции точек в аксонометрических проекциях обозначаются
- 17. СВОЙСТВА ЕВКЛИДОВА ПРОСТРАНСТВАС позиции теории множеств
- 18. Вместо выражений «точка А лежит на
- 19. Отношения принадлежности между элементами евклидова пространства могут
- 20. 2. Две различные точки А и В
- 21. 4. Если две точки А и В,
- 22. 5. Две прямые, принадлежащие одной плоскости, могут
- 23. Предложение 5 утверждает, что в евклидовой плоскости
- 24. Этапы конструирования, изготовления и реализации изделияпревратить физическую
- 25. ПЕРЕРЫВ
- 26. Центральное проецированиеПри заданных плоскости проекции и центре
- 27. Центральное проецирование
- 28. Основные свойства центрального проецированияТочка проецируется в точку;
- 29. Параллельное проецированиеЕсли направление проецирования перпендикулярно плоскости проекций, то проекции называются прямоугольными или ортогональными, иначе - косоугольными
- 30. Основные свойства параллельного проецированияТочка проецируется в точку;
- 31. Основные свойства параллельного проецированияПараллельные проекции взаимно параллельных
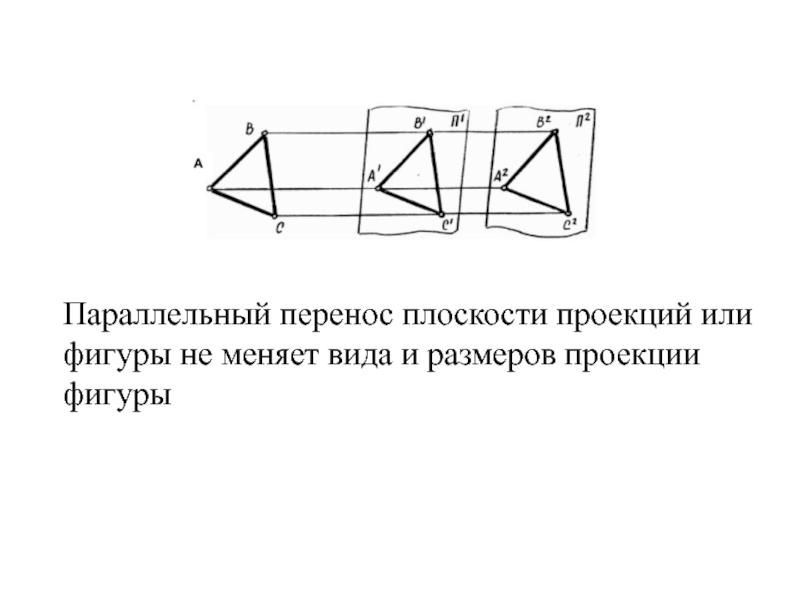
- 32. Параллельный перенос плоскости проекций или фигуры не меняет вида и размеров проекции фигуры
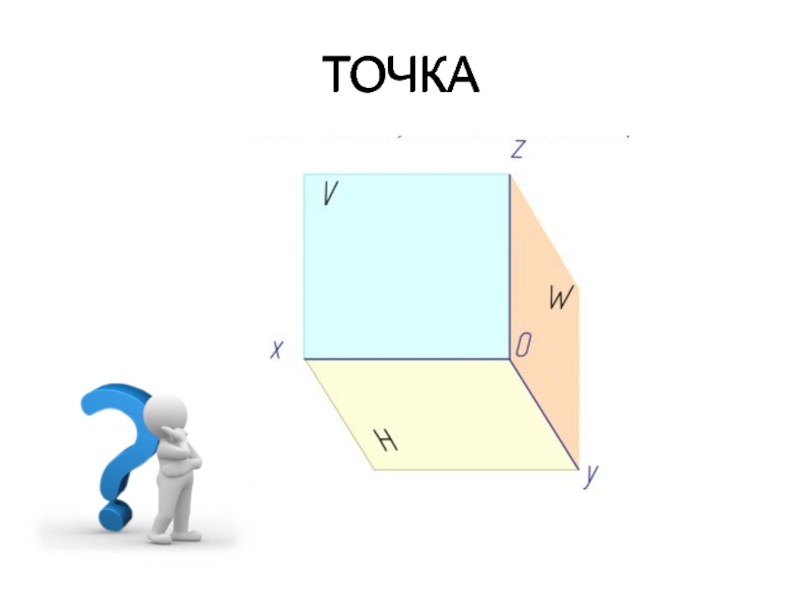
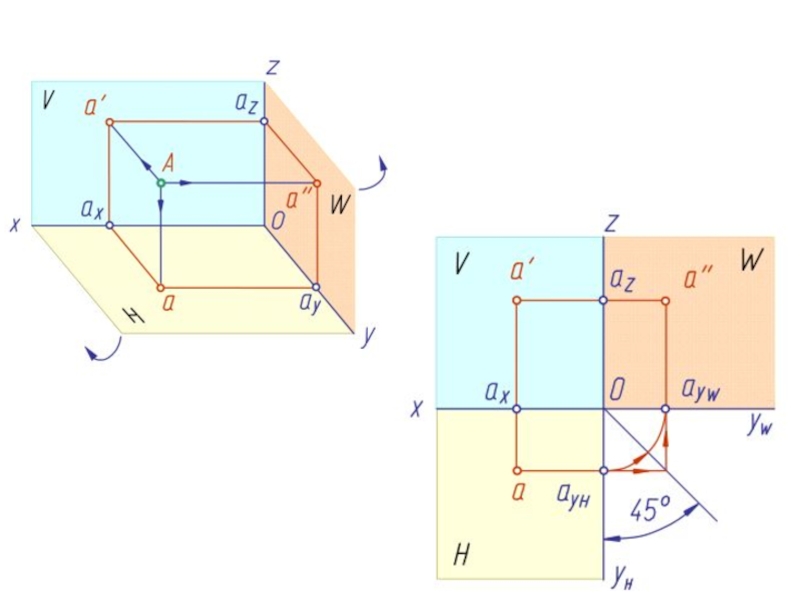
- 33. ТОЧКАТОЧКА
- 34. Слайд 34
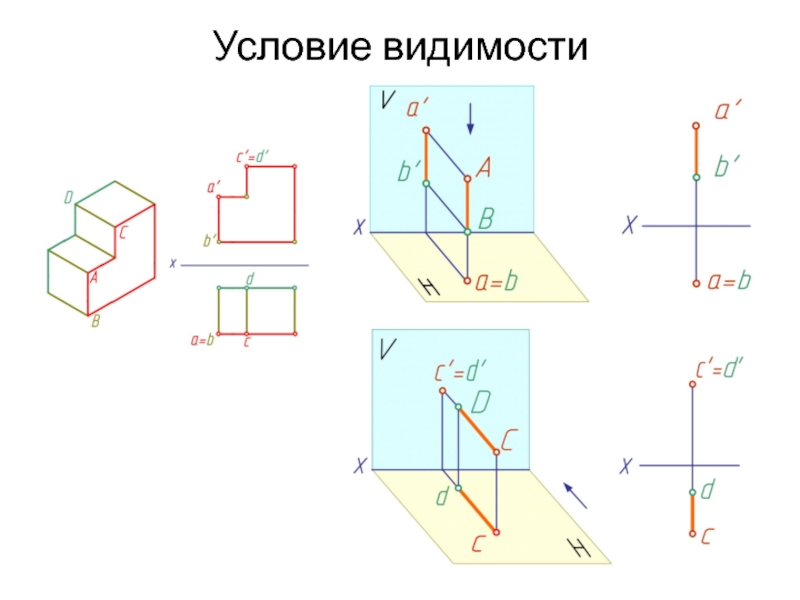
- 35. Условие видимости
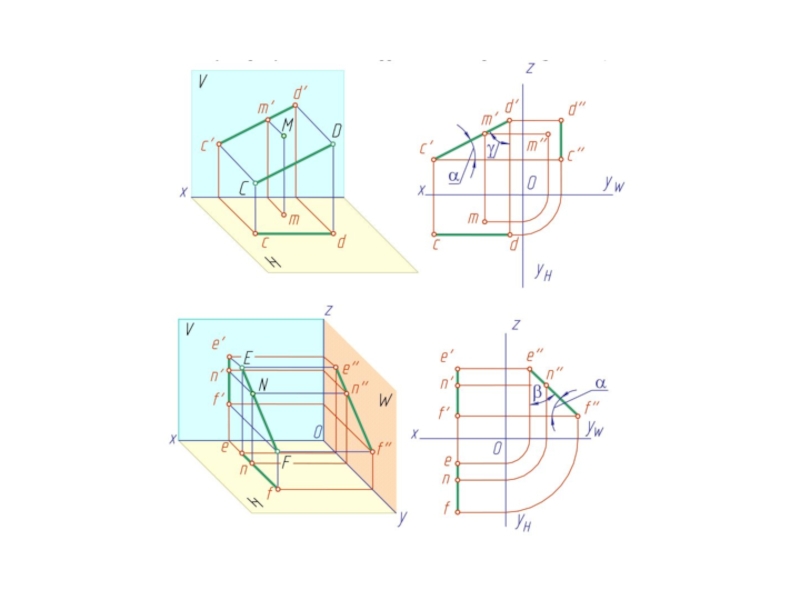
- 36. Слайд 36
- 37. Слайд 37
- 38. Слайд 38
- 39. Слайд 39
- 40. Слайд 40
- 41. Слайд 41
- 42. Слайд 42
- 43. Слайд 43
- 44. Скачать презентанцию
Цель курсаИзучение основных правил и требований к порядку разработки, оформления и обращения конструкторской документации
Слайды и текст этой презентации
Слайд 2Цель курса
Изучение основных правил и требований к порядку разработки, оформления
и обращения конструкторской документации
Слайд 3Геометрический язык
По С.А. Фролову геометрический язык состоит из обозначений и
символов, принятых в курсе математики :
- обозначения геометрических фигур и
отношений между ними;обозначения логических операций.
Особое внимание необходимо уделять символам, которые применяются для обозначения проекций геометрических фигур.
Слайд 4Основные понятия и определения
Плоскостью называется поверхность, образуемая движением примой линии,
которая движется параллельно самой себе на неподвижной направляющей.
Поверхность – множество
последовательных положений движущейся линииСлайд 5Обозначение геометрических фигур
Геометрическая фигура обозначается — Ф.
2. Точки обозначаются прописными
буквами латинского алфавита или
арабскими цифрами:
(курсив)
А, В, С, D, ..., L, M, N, ..(прямой шрифт) 1,2, 3,4,..., 12, 13, 14,...
Слайд 63. Линии, произвольно расположенные по отношению к плоскостям проекций, обозначаются
строчными буквами латинского алфавита:
а, b, с, d, l, m, n,
...Линии уровня обозначаются:
h — горизонталь;
f — фронталь.
Для прямых используются также следующие обозначения: (AB) — прямая, проходящая через точки А и В; [AB) - луч с началом в точке А;
[AB] — отрезок прямой, ограниченный точками А и В.
Слайд 74. Поверхности обозначаются строчными буквами греческого алфавита:
— альфа, β
— бэта, — γ гамма, σ — cигма, …, —
кси, — эта, ν – ню (ни), …Чтобы подчеркнуть способ задания поверхности, следует указывать геометрические элементы, которыми она определяется, например:
(а || b) — плоскость определяется параллельными прямыми а и b;
Слайд 85. Углы обозначаются:
ABC — угол с вершиной в
точке В, а также
a°, β°,..., φ°, ...6. Угловая величина (градусная мера) обозначается знаком , который ставится над углом:
ABC — величина угла ABC, φ° — величина угла φ.
Прямой угол отмечается квадратом с точкой внутри .
Слайд 97. Расстояния между геометрическими фигурами обозначаются двумя вертикальными отрезками — |
| .
Например:
|АВ| — расстояние между точками А и В (длина
отрезка AB);|Аа| — расстояние от точки А до линии а;
|А|— расстояние от точки А до поверхности ;
|аb| — расстояние между линиями а и b;
|β| — расстояние между поверхностями и β.
Слайд 108. Для плоскостей проекций приняты обозначения:π1, и π2,
где π1 —
горизонтальная плоскость проекций;
π2 — фронтальная плоскость проекций.
При замене плоскостей проекций
или введении новых плоскостей последние обозначают π3, π4 и т.д.Слайд 1110. Проекции точек, линий, поверхностей, любой геометрической фигуры обозначаются теми
же буквами (или цифрами), что и оригинал, с добавлением верхнего
индекса, соответствующего плоскости проекции, на которой они получены:A', B', C', D', ..., L', M', N', ... — горизонтальные проекции точек; А", В", С", D", ..., L", M", N", ... — фронтальные проекции точек; a', b', c', d', ...,l, m', n', ... — горизонтальные проекции линий; а", b", с", d",...,l, m", n", ... — фронтальные проекции линий; ', β', γ', δ', ..., ζ', ', ν', ... — горизонтальные проекции поверхностей; ", β", γ", δ", ..., ζ", ", ν",... — фронтальные проекции поверхностей.
Слайд 1212. Следы прямых (линий) обозначаются заглавными буквами, с которых начинаются
слова, определяющие название (в латинской транскрипции) плоскости проекции, которую пересекает
линия, с подстрочным индексом, указывающим принадлежность к линии.Например: На — горизонтальный след прямой (линии) а;
Fa — фронтальный след прямой (линии) а.
Слайд 1311. Следы плоскостей (поверхностей) обозначаются теми же буквами, что и горизонталь
или фронталь, с добавлением подстрочного индекса 0, подчеркивающего, что эти линии
лежат в плоскости проекции и принадлежат плоскости (поверхности) .Так: h0а — горизонтальный след плоскости (поверхности) ;
f0а — фронтальный след плоскости (поверхности) .
Слайд 1413. Последовательность точек, линий (любой фигуры) отмечается подстрочными индексами 1,
2, 3, … , n:
А1, А2,А3, …, Аn;
а1, а2,а3,
… ,аn –последовательность линий 1, 2, 3,..., n;- последовательность поверхностей
Ф1, Ф2, Ф3,..., Фn – последовательность фигур
Вспомогательная проекция точки, полученная в результате преобразования для получения действительной величины геометрической фигуры, обозначается той же буквой с подстрочным индексом 0:
A0, B0, С0, D0, ...
Слайд 15Аксонометрические проекции
14. Аксонометрические проекции точек, линий, поверхностей обозначаются теми же
буквами, что и натура с добавлением верхнего индекса 0 :
A0,B0,
C0, D0, ...1°, 2°, 3°, 4°,...
a0, b0,c0,d0 … ;
0, β0, γ0,δ0,... ;
Слайд 16Вторичные проекции точек в аксонометрических проекциях обозначаются путем добавления верхнего
индекса 1:
А10, В10, С10, D10,...
110, 210, 310, 410,...
a10, b10 ,
с10, d10,...10, β 10, γ 10, δ 10,...
Слайд 17 СВОЙСТВА ЕВКЛИДОВА ПРОСТРАНСТВА
С позиции теории множеств геометрическая фигура есть
не пустое множество.
Точки, прямые и плоскости евклидова пространства находятся в
определенном взаимоотношении, которое может быть обозначено словом принадлежность или инцидентность.Термин «инцидентность» заменяет такие понятия, как «лежать на», «проходить через».
Слайд 18 Вместо выражений «точка А лежит на плоскости а», «прямая
а проходит через точку В» можно употреблять выражения «точка А
инцидентна (принадлежит) плоскости а», «точка В инцидентна (принадлежит) прямой а».В символической форме эти выражения можно записать А ; В а.
Слайд 19Отношения принадлежности между элементами евклидова пространства могут быть выражены следующими
предложениями.
1. Если точка А принадлежит прямой а, а прямая а
принадлежит плоскости , то точка А принадлежит плоскости :А а А .
Слайд 202. Две различные точки А и В всегда принадлежат одной
и той же и только одной прямой а или каждой
прямой а принадлежат, по крайней мере, две точки А и В:(A, В) (А В) (1a) (А, В).
Три различные точки А, В и С, не принадлежащие одной прямой, принадлежат одной и той же и только одной плоскости:
(А, В,С)(A В С) (А, В, С а) (1 a)( э А, В, С).
Слайд 214. Если две точки А и В, принадлежащие прямой а,
принадлежат плоскости , то прямая а принадлежит плоскости :
(А, B)(A
B)(A, В а) (А, В ) (а ).Кроме приведенных выше, могут быть сформулированы и другие предложения принадлежности для элементов евклидова пространства. К таким предложениям, в частности, относятся:
Слайд 225. Две прямые, принадлежащие одной плоскости, могут принадлежать одной точке,
но этого может и не быть.
6. Две плоскости могут принадлежать
одной и той же прямой, но этого может и не быть.7. Плоскость и не принадлежащая ей прямая могут принадлежать одной точке, но этого может и не быть.
Последние три предложения по существу перефразируют аксиому о параллельности.
Слайд 23Предложение 5 утверждает, что в евклидовой плоскости две прямые либо
пересекаются (принадлежат одной точке), либо не имеют общей точки —
в этом случае они называются параллельными. Аналогично предложение 6 говорит о том, что в евклидовом пространстве две плоскости либо пересекаются (принадлежат одной прямой) либо они параллельны, а предложение 7 - о том, что прямая, не принадлежащая плоскости, либо пересекает ее (прямая и плоскость принадлежат одной точке), либо они параллельны.Слайд 24Этапы конструирования, изготовления и реализации изделия
превратить физическую или мысленную модель
изделия в графическую;
графическую модель описать аналитически;
выполнить численный анализ изделия
на конструкторскую и экономическую обосно-ванность графической модели изделия.разработать математическую модель управления процессом разработки изделия, модификации и реализации.
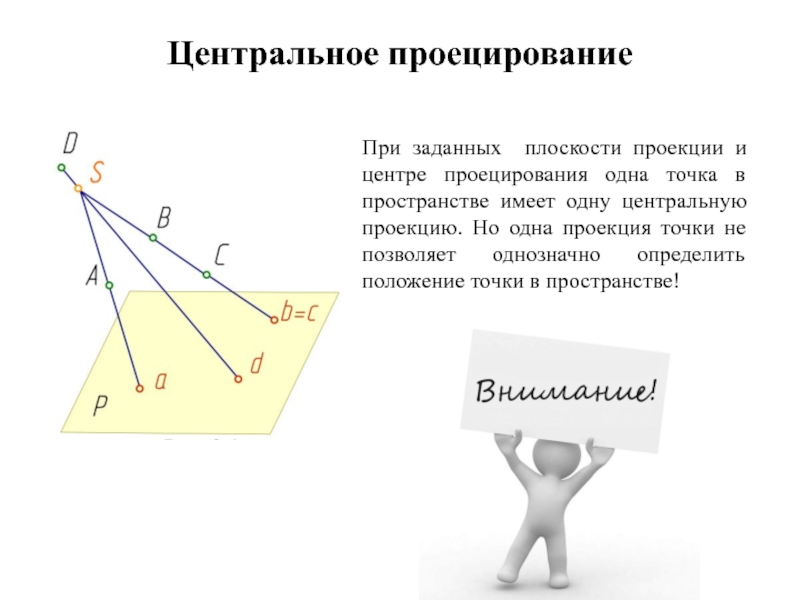
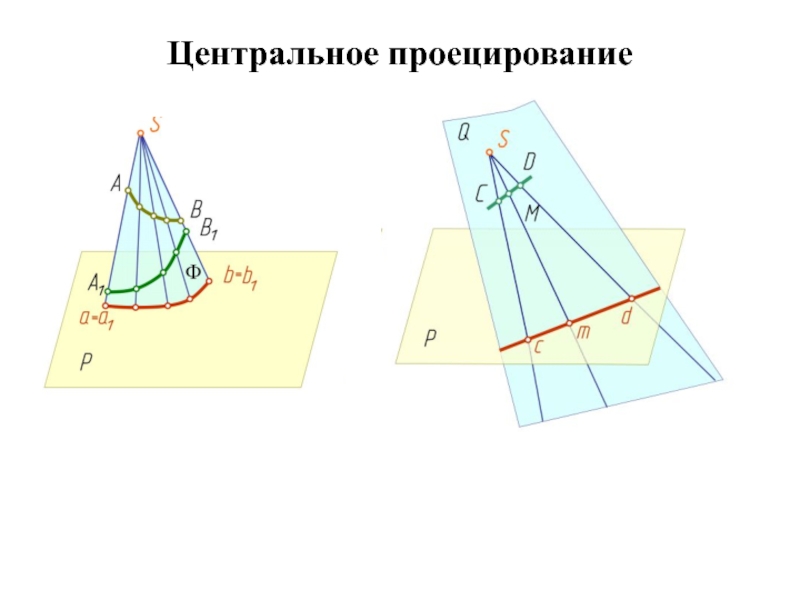
Слайд 26Центральное проецирование
При заданных плоскости проекции и центре проецирования одна точка
в пространстве имеет одну центральную проекцию. Но одна проекция точки
не позволяет однозначно определить положение точки в пространстве!Слайд 28Основные свойства центрального проецирования
Точка проецируется в точку;
Прямая, не проходящая
через центр проецирования, проецируется в прямую (иначе в точку);
Плоская фигура
не принадлежащая проецирующей плоскости, проецируется в двумерную фигуру (иначе в прямую линию).Трехмерная фигура проецируется в двумерную.
Слайд 29Параллельное проецирование
Если направление проецирования перпендикулярно плоскости проекций, то проекции называются
прямоугольными или ортогональными, иначе - косоугольными
Слайд 30Основные свойства параллельного проецирования
Точка проецируется в точку;
Прямая проецируется в
прямую;
Если точка принадлежит линии, то проекция этой точки принадлежит проекции
линии (свойство принадлежности).Если отрезок прямой делится точкой в некотором отношении, то проекция отрезка делится проекцией этой точки в том же отношении.
Слайд 31Основные свойства параллельного проецирования
Параллельные проекции взаимно параллельных прямых параллельны, о
отношение длин отрезков этих прямых равно отношению длин их проекций;
Плоская фигура, параллельная плоскости проекций, проецируется на эту же плоскость в такую же фигуру;
Параллельный перенос фигуры в пространстве или плоскости проекций не изменяет вида или размеров проекций.