функции на бесконечности?
А, что такое бесконечность?
Бесконечность — используется для характеристики безграничных,
беспредельных, неисчерпаемых предметов и явлений, в нашем случае характекстика чисел. Бесконечность –сколь угодно большое(малое), безграничное число.
Если рассмотреть координатную плоскость то ось абсцисс(ординат) уходит на бесконечнсть, если ее безгранично продолжать влево или вправо(вних или вверх).
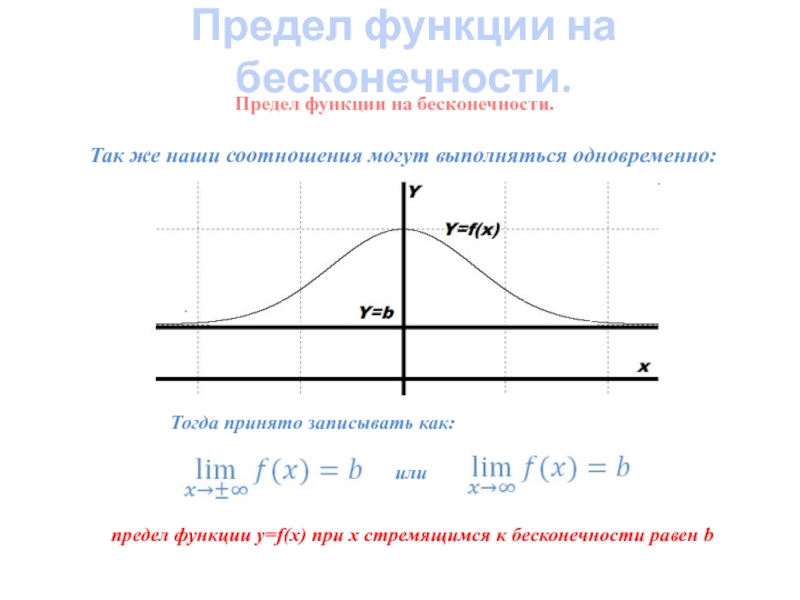
Предел функции на бесконечности


![Урок на тему: Предел функции на бесконечности Посмотрим немного другой случай:Пусть у нас есть функция y=f(x), область определения Посмотрим немного другой случай:Пусть у нас есть функция y=f(x), область определения нашей функции содержит луч (-∞; a],](/img/thumbs/d71f9aef3ad91554ef56209f5026fe53-800x.jpg)