Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Урок по алгебре Иррациональные уравнения
Содержание
- 1. Урок по алгебре Иррациональные уравнения
- 2. Повторение Среди пар уравнений найдите пары равносильных:
- 3. Повторение Определите, какое из двух уравнений является следствие другого:
- 4. Повторение Арифметическим квадратным корнем из числа
- 5. Что общего в этих уравнениях?=2 +
- 6. Иррациональные уравнения
- 7. Определение Иррациональными называются уравнения, в которых переменная содержится под знаком корня (радикала).Примеры:
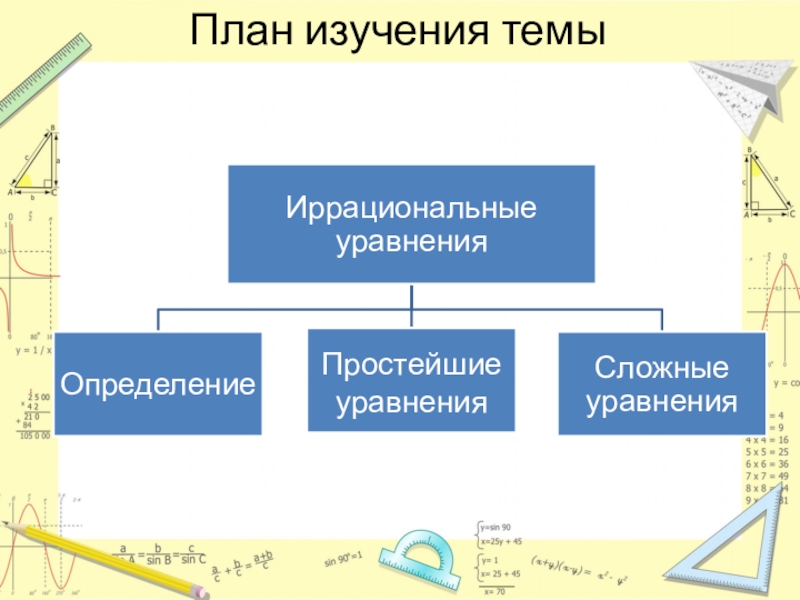
- 8. План изучения темы
- 9. Какие из уравнений не являются иррациональными?
- 10. Идея решенияГлавный способ избавиться от корня и
- 11. Простейшие иррациональные уравнения
- 12. Запомни!При возведении обеих частей уравнения •
- 13. Слайд 13
- 14. Решение уравнения1) а0, то Пример:
- 15. Решение уравнения1 способ2 способ
- 16. Вывод Уравнение вида
- 17. Решение уравнения1 способ2 способ
- 18. Вывод Уравнение вида
- 19. Самостоятельная работаIIIIIIIV
- 20. Скачать презентанцию
Повторение Среди пар уравнений найдите пары равносильных:
Слайды и текст этой презентации
Слайд 4Повторение
Арифметическим квадратным корнем из
числа а называется неотрицательное число
b, квадрат которого равен а
a=b2Слайд 7Определение
Иррациональными называются
уравнения, в которых переменная
содержится под
знаком корня (радикала).
Примеры:
Слайд 10Идея решения
Главный способ избавиться от корня и получить рациональное уравнение
– возведение обеих частей уравнения в одну и ту же
степень, которую имеет корень, содержащий неизвестное.Основная идея решения иррационального уравнения состоит в сведении его к рациональному алгебраическому уравнению, которое либо равносильно исходному иррациональному уравнению, либо является его следствием.
Слайд 12Запомни!
При возведении обеих частей уравнения
• в четную степень
(показатель корня – четное число) – возможно появление постороннего
корня (проверка необходима)
• в нечетную степень (показатель корня –
нечетное число) – получается уравнение,
равносильное исходному (проверка не нужна)
Слайд 13 Запомни!
Решая иррациональные
уравнения с помощью равносильных преобразований
(проверка не нужна)
Слайд 16Вывод
Уравнение вида
решается:
Возведением в квадрат обеих частей
равенства с последующей проверкой;Осуществляется переход к системе
равносильной данному уравнению, т.е.
Слайд 18Вывод
Уравнение вида
решается:
Возведением в квадрат обеих частей
равенства с последующей проверкой;Осуществляется переход к системе равносильной данному уравнению, т.е.