Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Вариациялық қатардың түрлері Орындаған:Досмұқамет Д.Б Тексерген: Абсатарова К.С
Содержание
- 1. Вариациялық қатардың түрлері Орындаған:Досмұқамет Д.Б Тексерген: Абсатарова К.С
- 2. Жоспар:1.Вариациялық қатар түрлері2.Гистограмма3.Вариациялық қатардың графигі
- 3. Вариация - бір жиынға енетін белгілердің ауытқу
- 4. Бір-бірінен толық бүтін сан мәндерімен ерекшеленетін сандар
- 5. Вариация қатарын ұйымдастыруға мысал келтірейік. Мысалы, шошқа
- 6. Вариациялық қатардың барлық жиіліктерінің қосындысы сұрып жиынның
- 7. Берілген мәліметтерді вариация қатарына орналастыру екі мақсат
- 8. Жоғарыдағы келтірілген мысалдағы мәліметтерді осы мақсатта төмендегі
- 9. Максималды вариант (варианттардың үлестірімдігі қалыпты (нормалдық) заңға
- 10. Минималды вариант үшін:
- 11. Вариациялық қатар мынадай түрге бөлінеді:Аралық қадамы бірдей
- 12. Аралық қадамы бірдей емес аралық вариациялық қатар
- 13. Ол үшін Стэрджесс формуласы қолданылады: к
- 14. Слайд 14
- 15. Сонымен қатар i-ші аралықтың жоғарғы мәні (i
- 16. Үздіксіз аралық қатарда негізгі параметр ретінде осы
- 17. Вариациялық қатардың графигіВариациялық қатардың бейне
- 18. Жоғарыда айтқандай, үлестірімділік кеңісі дискретгі және үздіксіз
- 19. Дискретті қатар үшін график тұрғызғанда, бірінші топтың
- 20. Шошқа фермасындағы аналықтардың өнімі, яғни торайлар саны
- 21. Осындай жағдайды болдырмау үшін «Алтын қиыс» ережесі
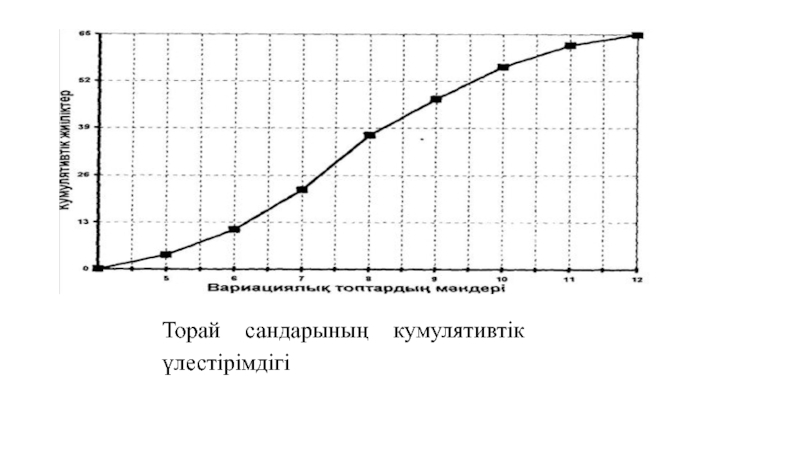
- 22. Торай сандарының кумулятивтік үлестірімдігі
- 23. Скачать презентанцию
Жоспар:1.Вариациялық қатар түрлері2.Гистограмма3.Вариациялық қатардың графигі
Слайды и текст этой презентации
Слайд 4Бір-бірінен толық бүтін сан мәндерімен ерекшеленетін сандар қатарын дискретті вариация
деп атайды.
Бір-бірінен кез келген бөлшек сандармен ерекшеленетін сандар қатарын үздіксіз
вариация деп атайды.Мысалға, дискретті вариация белгілері үшін бір отардағы қойлар және ешкілер саны, бір жанұядағы адамдар саны және т.б., ал үздіксіз вариация белгілері ретінде тәуліктегі уақыт, бір отардағы қойлардың салмақтары және т.с.с. алынады.
Слайд 5Вариация қатарын ұйымдастыруға мысал келтірейік. Мысалы, шошқа фермасында 65 мегежін
тіркелді. Әр аналық шошқадан алынған торайлар саны мынадай болсын: 8,
9, 12, 10, 6, 7; 11, 8, 6, 8, 9, 12, 7, 6, 11,5, 8, 8, 6, 12,5, 9, 7, 10, 6, 8, 9, 11,8, 710, 9,5, 10, 8, 11, 6, 7, 9, 8, 6, 11, 7, 10, 8, 9, 7, 8, 8, 10, 9, 7, 11, 10, 8, 7, 8, 10, 7, 9, 10, 8,5,7, 9.Бақылау нәтижесін тіркеу ретімен және осы жиында варианттардың қайталану санымен берілген мәліметтерді бір қатарға орналастырайық:
варианттар хі 8 9 12 10 6 7 11 5
вариант саныfi15 10 3 9 7 11 6 4
Сөйтіп, вариация қатарын алдық. Әр варианттың қанша рет берілген жиында кездесетінін көрсететін сан жиілік немесе вариант өлшемі деп аталады.
Слайд 6Вариациялық қатардың барлық жиіліктерінің қосындысы сұрып жиынның мөлшеріне тең, яғни:
Жиілік (өлшем) тек абсолюттік шамамен емес, қатынастық мөлшерде - меншікті
салмақпен немесе пайызбен, яғни осы көрсеткіш жиынының жалпы санына қатынасымен өлшенуі мүмкін. Мұндай жағдайда өлшемдер қатынастық жиілік немесе жиілгіштер деп аталады. Жиілгіштердің жалпы қосындысы бірге тең, яғни =1,егер жиіліктің бақылаудың жалпы санына п қатнасы пайызбен өрнектелсе,онда
Слайд 7Берілген мәліметтерді вариация қатарына орналастыру екі мақсат үшін жасалынады. Оның
бірі - жалпы сандық сипаттамаларды, оның ішінде орташа шаманы және
вариация көрсеткішін есептеуді тездету және оңайлату болса, ал екінші мақсаты - қарастырылып отырған белгінің вариация заңдылықтарын анықтауды көздейді.Жоғарыдағы келтірілген вариациялық қатар бірінші мақсатгы қанағаттандырғанымен, екінші мақсатты қанағаттандырмайды. Берілген бөлініп таралу қатары қойылған талаптарға жауап беру үшін оны белгінің өсу ретімен қайта орналастыру керек.
Қатарды реттеу іс-әрекеті, яғни варианттарды өсу немесе кему ретімен орналастыру жұмысы қатарды рангілеу (ранжировать) бойынша орналастыру деп аталады.
Слайд 8Жоғарыдағы келтірілген мысалдағы мәліметтерді осы мақсатта төмендегі ретпен орналастырамыз:
варианттар х і 5 6 7 8 9 10 11
12жиіліктер fi 4 7 11 15 10 9 6 3
Енді, алынған вариациялық қатар бірінші және екінші мақсатқа жетуді қамтамасыз етеді.
Слайд 9
Максималды вариант (варианттардың үлестірімдігі қалыпты (нормалдық) заңға бағынса немесе оған
жақын жатса) үшін мынадай формула қолданылады:
Мұндағы tn - максималды вариант хп жиынға жататынын
дәлелдейтін критерийі;
хn - максималды вариант;
хп-1 - максималды варианттың алдындағы вариант;
х2-минималды варианттан кейіигі вариант.
Слайд 10Минималды вариант үшін:
Мұндағы t1 - минималды вариант х1жиынға жататынын
дәлелдейтін критерийі;
х2- минималды варианттан кейінгі вариант;
хn-1 - максималды варианттың хп алдындағы вариант.
Слайд 11Вариациялық қатар мынадай түрге бөлінеді:
Аралық қадамы бірдей вариациялық аралық қатар.
Әрбір аралық вариациялық катардың жоғарғы мәні келесі аралық вариациялық қатардың
төменгі мәніне сәйкес келеді. Мұндай тәсіл өте ыңғайлы және математикалық статистикада жиі қолданылады;-аралық қадамы бірдей емес аралық вариациялық қатар.
Аралық қадамы бірдей емес аралық вариациялық қатар тәжірибеде жиі қолданылмайды. Сондықтан көп жағдайда міндетті түрде аралық кадамы бірдей вариациялық аралық қатар құрылады. Мүндай тәсіл белгінің вариациялық заңдылықтарын аңғаруға, вариациялық қатардың қорытынды сипаттамаларын есептеуге және вариациялық қатарды басқа қатарлармен салыстыруға көмектеседі.
Слайд 12Аралық қадамы бірдей емес аралық вариациялық қатар тәжірибе-де жиі қолданылмайды.
Сондықтан көп жағдайда міндетті түрде аралық кадамы бірдей вариациялық аралық
қатар құрылады. Мүндай тәсіл белгінің вариациялық заңдылықтарын аңғаруға, вариациялық қатардың қорытынды сипаттамаларын есептеуге және вариациялық қатарды басқа қатарлармен салыстыруға көмектеседі.Бірдей аралық вариациялык қатарды құру үшін бірінші кезекте аралық қадамды белгілеу маңызды. Аралық қадам немесе кейде аралық вариация қатарының ені деп атайды. Әрі қарай тексте кадам делінеді. Қадам тым үзын немесе қысқа болса, қарастырылып отырған жиынды сипаттайтын вариациялық заңдылық өзгереді де, зерттеуші дұрыс шешім қабылдамауы мүмкін. Негізінде қадамның оптималды мәнін табу үшін сұрыптық жиын, оның максималды және минималды вариантының аралығында класқа (аралыққа) к бөлінеді.
Слайд 13Ол үшін Стэрджесс формуласы қолданылады:
к =1 + 3,322∙1g
п.
Аралық вариация қадамы мына формуламен есептелінеді:
Мұндағы хmax және xmin - максималды және минималды
варианттар;
п - сүрыптық жиын мүшелерінің саны.
Слайд 15Сонымен қатар i-ші аралықтың жоғарғы мәні (i + 1)-ші ара-
лықтың төменгі мәніне сәйкес болғандықтан, аралық жиілікті есептегенде оның төменгі
мәніне тең немесе үлкен және жоғарғы мәнінен кіші жиын мәндері алынады.Қадам өлшем бірлігі алғашқы белгінің өлшем бірлігінің дәлме-дәлдігіне сәйкес келгені жөн. Мысалы, (п = 80) сиыр сүтінің майлылық мөлшерінің вариациясы 3,30-дан 4,51% аралығында. Олай болса (1.3) формуламен есептелген аралық кадам.
z≠1, демек аралық вариациялық қатар үздіксіз бөлініп тара-
лады.
Слайд 16Үздіксіз аралық қатарда негізгі параметр ретінде осы ара- лықтың орта
шамасы алынады, яғни:
Нәтижесінде үздіксіз аралық қатар үздікті қатарға айналады. Мұндай түрлендірудің қажеттігі орташа дисперсияны есептеуге байланысты туады.
Гистограмма - бұл аралық үздіксіз вариациялық қатардың биіктігі әр түрлі тікбұрышты төрт бұрышпен салынған көрінісі. Абсцисса өсіне белгілердің өзгеріс аралықтары отырғызылған, ал тікбұрышты төрт бұрыштың биіктігі аралық топтардың жиілігімен сәйкестендірілген.
Слайд 17 Вариациялық қатардың графигі
Вариациялық қатардың бейне көрінісін байқау үшін
оның графигін тұрғызады. Ол үшін координаттар жүйесі тұрғызылады да, абсцисса
өсіне вариация қатарының мәндерін, ал ордината өсіне оларға сәйкес жиілікті (немесе жиілгішті) отырғызады.Дискретті вариациялық қатар болса, биіктігі жиілігіне сәйкес келетіндей етіп әр вариациялық дискретті белгіге, яғни абсцисса осіне тік бұрышты сызық жүргізіледі. Осы тікбұрышты сызықтарының төбелерін қосып, көпбұрыш алынады. Оны үлестірімділік кеңісі (полигон распределения) деп атайды да, төбелерді қосқан сызықтарды вариация қисығы немесе вариация жиілігінің үлестірімділік қисығы дейді.
Слайд 18Жоғарыда айтқандай, үлестірімділік кеңісі дискретгі және үздіксіз вариациялық қатарға да
түргызылуы мүмкін. Кеңістің барлық ординаттарының кез келген гистограмманы кеңіске айналдыруға
болады. Ол үшін барлық тікбұрышты төртбұрыштың жоғарғы қабырғаларының ортасын бір сызықпен қосамыз, нәтижесінде кеңіс алынады.Вариациялық қатар бойынша жиіліктер жиынымен тұрғызылған график кумулята деп аталады. Ол белгінің вариациялық заңдылығының функциясын бейнелейді. Топ өсу ретімен жиілік қосындыларынан құрылған графикті кумулята деп атайды.
Слайд 19Дискретті қатар үшін график тұрғызғанда, бірінші топтың жиілігінен басталып жиіліктер
жинала береді де, сол жиынның мәніне сәйкес ординаталар төбелерін түзу
сызықпен қоса береміз, нәтижесінде кумулята алынады.Үздіксіз вариациялық қатар үшін график нөлден басталып сызықтың екінші ұшы бірінші топтың жиілігіне сәйкес келсе, ал келесі екі топтың жиіліктерінің қосындысының мәніне сәйкестендіріп әрі қарай осы ретпен график тұрғызыла береді. Кумулятивтік қисықты кейде жиілік жиындарының кеңісі деп атайды.
Слайд 20Шошқа фермасындағы аналықтардың өнімі, яғни торайлар саны мынадай кумулятивтік қисықпен
сипатталады (1.3-сурет):
Жиілік/: 4 7 11 15 10 9 6 3
Кумуляталар 2/'
4 11 22 37 47 56 62 65Графикті тұрғызу жауапты істің бірі екенін атап өткеніміз жөн. Абсцисса өсінде вариация қатарының мәнінің масштабы дұрыс қойылмауы себепті, кейде ол сүйір немесе доғал төбелі болуы мүмкін. Мұндай жағдайда оқылып отырған белгінің заңдылығы қатты өзгеріске ұшырайды да, график зерттеушіге дұрыс шешім қабылдауға ықпал жасамайды.