Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Важные теоремы о непрерывных функциях
Содержание
- 1. Важные теоремы о непрерывных функциях
- 2. Важные теоремы о непрерывных функцияхЕсли на отрезке
- 3. Производная функцииПравая и левая производныеФункция дифференцируема в
- 4. Предельные издержки производстваРассмотрим ситуацию: пусть y -
- 5. Другой пример - категория предельной выручки
- 6. Задача о касательной к графику функцииxyС∆х=х-х0∆f(x) = f(x) - f(x0)
- 7. Геометрический смысл производной. Уравнение касательной к функции.
- 8. Дифференциал функцииграфик дифференцируемой функции в окрестности каждой
- 9. Основные правила дифференцированияЕсли функции y = f (x) и z = g (y) дифференцируемы в точках x0 и y0 = f (x0) соответственно, то
- 10. Таблица производных
- 11. Примеры дифференцированияy=(3x3 -2x+1) × sin x. y'=(3x3 -2x+1)' × sin x + (3x3 -2x+1) × (sin
- 12. Производные 2го и более высоких порядковКогда мы
- 13. Некоторые теоремы о дифференцируемых функцияхЕсли функция имеет
- 14. Применение производных к исследованию функцийПризнак монотонности: если
- 15. Применение производных к исследованию функций: выпуклость и
- 16. Точки перегибаНеобходимое условиеДостаточное условие: f(x) непрерывна и
- 17. Исследование функцийНайти область определения и область значений
- 18. Асимтоты функциипрямые линии, к которым неограниченно приближается
- 19. Пример исследования функцииООФ: вся осьНепериодическаяНечетнаяВертикальных асимптот нетMax/min - нетНаклонные асимптоты:y=x
- 20. Раскрытие неопределенностей с помощью производных. Правило Лопиталя.предел
- 21. Эластичность спросаПереход к пределу:
- 22. Максимизация прибылиДоход - затраты на производство (издержки)Условие максимума:Предельный доход = предельным издержкам
- 23. Первообразная функции. Неопределенный интеграл.Функция F(x) называется первообразной
- 24. Свойства неопределенного интеграла
- 25. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Математика
1 семестр
встреча №2
Лектор: Шаталина Евгения Сергеевна
Литература: «Математика для
экономистов»,
Слайд 2Важные теоремы о непрерывных функциях
Если на отрезке [a,b] задана непрерывная
функция f(x), то для любого числа M, такого что f(a)≤M≤f(b)
найдется число СЄ[a,b] , такое что f(C)=MЕсли функция задана и непрерывна на отрезке [a,b], то она ограничена на этом отрезке (теорема Вейерштрасса)
Если функция задана и непрерывна на отрезке [a,b], то она принимает на этом отрезке наибольшее и наименьшее значение (теорема Вейерштрасса 2)
Слайд 3Производная функции
Правая и левая производные
Функция дифференцируема в точке,
если в
ней существует производная функции,
то есть правая и левая производные
функции в этой точке равныПример недифференцируемой функции: |x| в точке x=0
Гладкая функция – имеет непрерывную производную
на всей области определения
Слайд 4Предельные издержки производства
Рассмотрим ситуацию: пусть y - издержки производства, а
х - количество продукции, тогда Δx- прирост продукции, а Δy
- приращение издержек производства.В этом случае производная
выражает предельные издержки производства и характеризует приближенно дополнительные затраты на производство
дополнительной единицы продукции,где MC – предельные издержки (marginal costs); TC – общие издержки (total costs); Q - количество.
Слайд 5
Другой пример - категория предельной выручки
(MR— marginal revenue)
— это дополнительный доход (не прибыль!!!), полученный при переходе от
производства n-ной к (n+1)-ой единице продукта.Она представляет собой первую производную от выручки:
При этом R= PQ, где R–выручка (revenue); P–цена (price).
Таким образом , ⇒ MR= P.
Предельная выручка
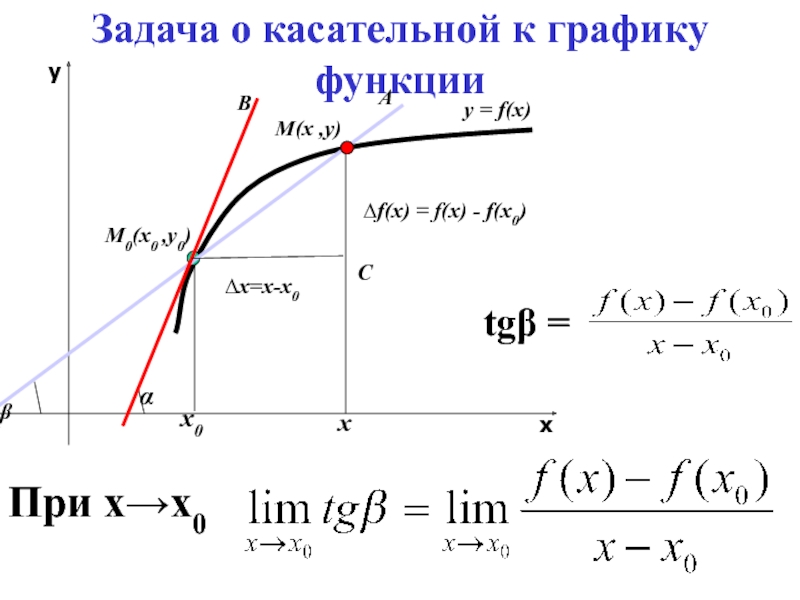
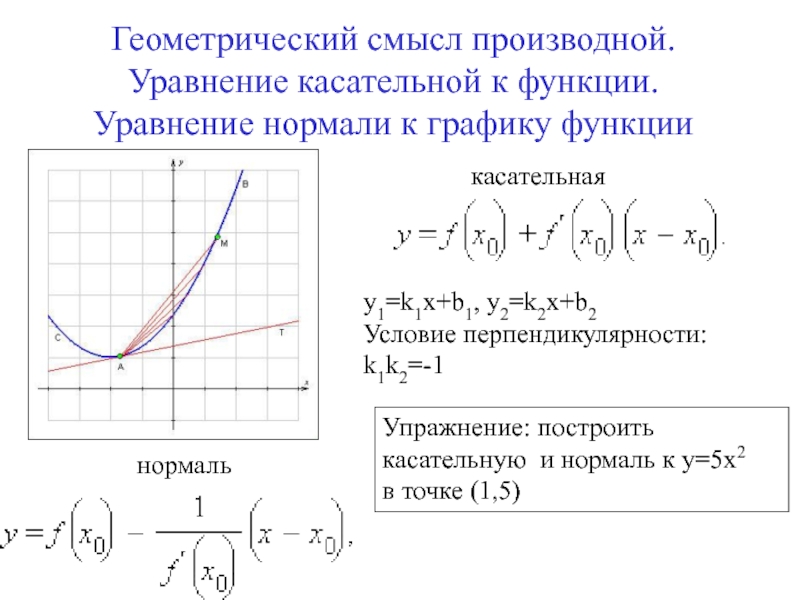
Слайд 7Геометрический смысл производной. Уравнение касательной к функции. Уравнение нормали к
графику функции
Упражнение: построить
касательную и нормаль к у=5x2
в точке
(1,5)касательная
нормаль
y1=k1x+b1, y2=k2x+b2
Условие перпендикулярности:
k1k2=-1
Слайд 8Дифференциал функции
график дифференцируемой функции в окрестности каждой своей точки сколь
угодно близко приближается к графику касательной
дифференциал функции df – это приращение ординаты
касательной к графику функции в данной точке при изменении абсциссы точки на dx Слайд 9Основные правила дифференцирования
Если функции y = f (x) и z = g (y) дифференцируемы в точках x0 и y0 = f (x0) соответственно, то сложная функция z = g (f (x)) дифференцируема в
точке x0, причем
Пусть в окрестности точки t0 определены функции x (t) и y (t), причем x (t) непрерывна и строго
монотонна. Пусть в этой окрестности существуют производные и Тогда сложная функция y = y (t (x)), где t (x) – функция, обратная x (t), дифференцируема по x, причем
Слайд 11Примеры дифференцирования
y=(3x3 -2x+1) × sin x.
y'=(3x3 -2x+1)' × sin x + (3x3 -2x+1) × (sin x)' = (9x2 -2)sin
x + (3x3 -2x+1)cos x.
y=ln sin x.
y' = (ln
u)' u (sin x)' x = Упражнение: Вычислить производную y=ln
Ответ:
.
Слайд 12Производные 2го и более высоких порядков
Когда мы дифференцируем функцию, каждой
точке этой функции мы ставим в соответствие некоторое число –
ее производную в данной точке. Таким образом, производная функции также является функцией.Если функция дифференцируема, то ее производную называют второй производной от f и обозначают :
Аналогичным образом задаются производные высших порядков. Если функция
f (n–1) дифференцируема, то ее производную называют производной n-го порядка f (n) функции f.
Важным применением второй производной является анализ выпуклости функции
Слайд 13Некоторые теоремы о дифференцируемых функциях
Если функция имеет в некоторой точке
х непрерывную производную, то и сама функция в этой точке
непрерывнаЕсли функция f(x) непрерывна на отрезке (a;b), и в точке x0 Є (a;b) принимает свое наибольшее (или наименьшее) значение,то f`(x0)=0 (теорема Ферма)
Если функция f(x) задана на отрезке [a;b], непрерывна на нем, дифференцируема на (a;b), и f(a)= f(b), то существует (.) С Є (a;b), такая что f`(С)=0. (теорема Ролля)
Слайд 14Применение производных к исследованию функций
Признак монотонности: если f(x) задана и
дифференцируема на (a;b), и f`(x)≥0 (f`(x)≤0) на (a;b), то f(x)
возрастает (убывает) на (a;b).Точки x, такие что f`(x)=0 – точки, подозрительные на экстремум (выполнено необходимое условие экстремума)
Достаточное условие экстремума: f`(x) в точке x0 меняет знак или f ``(x0)=0
Слайд 15Применение производных к исследованию функций: выпуклость и точки перегиба
Непрерывная на
отрезке [a; b] функция f (x) называется выпуклой вверх на этом отрезке, если для любых точек x1 и x2 из этого отрезка
Другими словами, если для любых точек x1 и x2 отрезка [a; b] секущая AB проходит под графиком функции f (x), то функция f выпукла вверх
Сформулируйте определение функции, выпуклой вниз
Точка, в которой меняется выпуклость функции, называется точкой перегиба
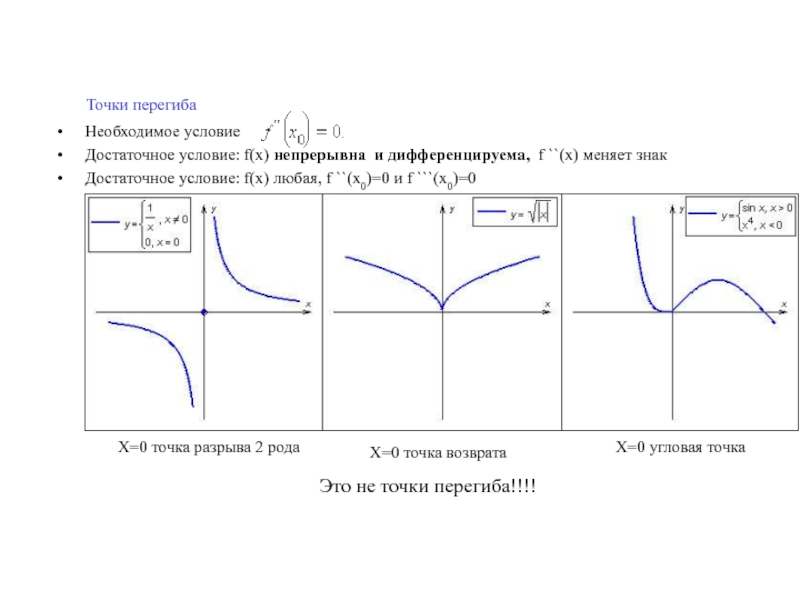
Слайд 16Точки перегиба
Необходимое условие
Достаточное условие: f(x) непрерывна и дифференцируема, f ``(x)
меняет знак
Достаточное условие: f(x) любая, f ``(x0)=0 и f ```(x0)=0
Это не точки перегиба!!!!
X=0 точка возврата
X=0 угловая точка
X=0 точка разрыва 2 рода
Слайд 17Исследование функций
Найти область определения и область значений функции.
Есть ли у
функции точки разрыва? Какого рода?
Выяснить, является ли функция четной f(-x) = f(x)?
Нечетной f(-x) = - f(x)?Выяснить, является ли функция периодической.
Найти точку пересечения графика функции с осью ординат.
Найти нули функции и промежутки знакопостоянства.
Вычислить 1 производную функции и определить точки, в которых могут существовать экстремумы.
Найти промежутки монотонности функции.
Определить экстремумы функции.
Вычислить вторую производную и, если необходимо, третью.
Определить точки перегиба.
Найти промежутки выпуклости функции.
Найти асимптоты графика.
Построить эскиз графика функции.
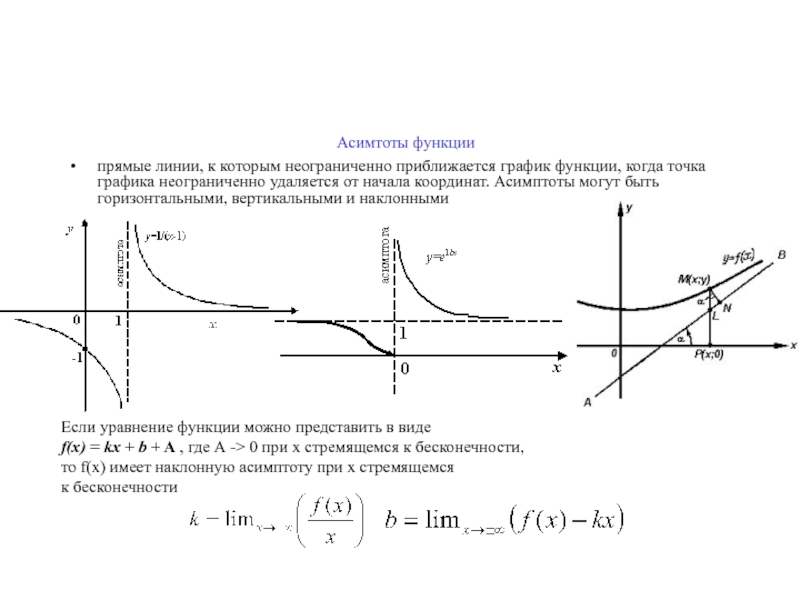
Слайд 18Асимтоты функции
прямые линии, к которым неограниченно приближается график функции, когда
точка графика неограниченно удаляется от начала координат. Асимптоты могут быть
горизонтальными, вертикальными и наклоннымиЕсли уравнение функции можно представить в виде
f(x) = kx + b + A , где А -> 0 при x стремящемся к бесконечности,
то f(x) имеет наклонную асимптоту при x стремящемся
к бесконечности
Слайд 19Пример исследования функции
ООФ: вся ось
Непериодическая
Нечетная
Вертикальных асимптот нет
Max/min - нет
Наклонные асимптоты:y=x
Слайд 20Раскрытие неопределенностей с помощью производных. Правило Лопиталя.
предел отношения двух бесконечно
малых или двух бесконечно больших величин равен пределу отношения их
производных , если он существуетПримеры
Контрпример
Слайд 22Максимизация прибыли
Доход - затраты на производство (издержки)
Условие максимума:
Предельный доход =
предельным издержкам
Слайд 23Первообразная функции. Неопределенный интеграл.
Функция F(x) называется первообразной для функции f(х)
на промежутке X, если для любого х е X функция
F(x) дифференцируема и выполняется равенство F‘(x) =f(x).Совокупность всех первообразных функций дляфункции f ix) на промежутке X называется неопределенным интегралом от функции fix) на этом промежутке и обозначается символом

![Важные теоремы о непрерывных функциях Важные теоремы о непрерывных функцияхЕсли на отрезке [a,b] задана непрерывная функция Важные теоремы о непрерывных функцияхЕсли на отрезке [a,b] задана непрерывная функция f(x), то для любого числа M,](/img/thumbs/816b4c17badbf5ca9a56228349862361-800x.jpg)










![Важные теоремы о непрерывных функциях Применение производных к исследованию функций: выпуклость и точки перегибаНепрерывная на отрезке [a; b] функция f (x) называется выпуклой вверх Применение производных к исследованию функций: выпуклость и точки перегибаНепрерывная на отрезке [a; b] функция f (x) называется выпуклой вверх на этом отрезке, если для любых](/img/thumbs/53c4cf9feba3f58d673ac38357ea954e-800x.jpg)