Слайд 1ВЕКТОРНАЯ АЛГЕБРА
1. Векторы, линейные операции и их алгебраические свойства.
Слайд 2Определения.
1) Прямая линия с заданным на ней направлением называется
осью.
2) Ось, на которой задано начало отсчёта (нуль) и
единица масштаба, называется числовой осью.
3) Отрезок, для которого определены начало и конец (направленный отрезок), называется геометрическим вектором (вектором).
4) Векторы называются коллинеарными, если они лежат на одной прямой, либо на параллельных прямых.
5) Векторы называются равными, если они коллинеарны, одинаково направлены и имеют одинаковую длину.
Слайд 3 Линейные операции над векторами
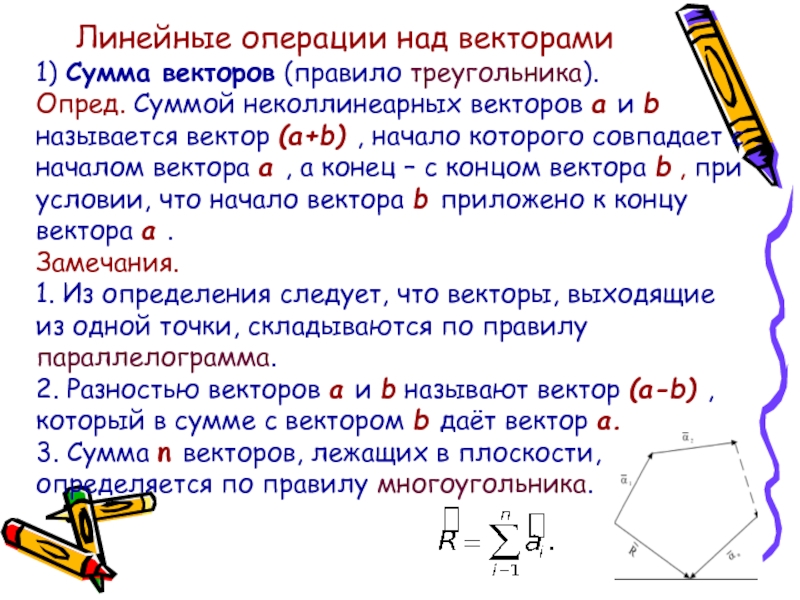
1) Сумма векторов (правило треугольника).
Опред. Суммой
неколлинеарных векторов а и b называется вектор (a+b) , начало
которого совпадает с началом вектора а , а конец – с концом вектора b , при условии, что начало вектора b приложено к концу вектора а .
Замечания.
1. Из определения следует, что векторы, выходящие из одной точки, складываются по правилу параллелограмма.
2. Разностью векторов а и b называют вектор (a-b) , который в сумме с вектором b даёт вектор а.
3. Сумма n векторов, лежащих в плоскости, определяется по правилу многоугольника.
Слайд 4Алгебраические свойства суммы
1. Коммутативность (перестановочность)
2. Ассоциативность (группировка)
3. Существование нулевого вектора
4.
Существование противоположного вектора
Слайд 52) Произведение вектора на вещественное число.
Опред. Произведением вектора а
и вещественного числа называется вектор
, который:
1. имеет длину ,
2. сонаправлен вектору а , при и противоположно направлен вектору а при
Алгебраические свойства произведения
1.
2.
3.
Слайд 6Лемма 1. Если вектор b коллинеарен вектору а, то найдется
число
.
Док-во: Отложим векторы на одной числовой оси, найдем их длины и составим отношение
Если векторы сонаправлены, то
если они направлены противоположно, то
Тогда, по определению произведения вектора на число, . Доказано.
Слайд 72. Линейная независимость векторов. Базис.
Определения.
Линейной комбинацией векторов
называется выражение
где коэффициенты
- некоторые числа.
2) Векторы называются линейно независимыми, если их линейная комбинация равна нулю только при условии, что все её коэффициенты равны нулю.
3) Векторы называются линейно зависимыми, если их линейная комбинация равна нулю, но при этом найдется хотя бы один ненулевой коэффициент.
4) Базисом в пространстве R3 называется любая тройка линейно независимых векторов.
Слайд 8Теорема 3. Необходимым и достаточным условием линейной зависимости двух
векторов является их коллинеарность.
Док-во: 1. Необходимость. Пусть векторы
линейно зависимы.
Тогда при условии
один из коэффициентов не равен нулю. Пусть
Отсюда . Но произведение вектора на число коллинеарно данному вектору, значит - коллинеарные векторы.
2. Достаточность. Пусть коллинеарны. Тогда по Лемме 1, найдется .
Отсюда получим
По определению, векторы линейно зависимы. Доказано.
Слайд 9Теорема 4. Необходимым и достаточным условием линейной зависимости трех векторов
является их компланарность.
Док-во: 1. Необходимость. Пусть векторы
линейно
зависимы.Тогда при условии
один из коэффициентов не равен нулю. Пусть
Отсюда .
Это равенство означает, что вектор есть диагональ параллелограмма, построенного на векторах .
Следовательно, все три вектора лежат в одной плоскости, т.е. компланарны.
2. Достаточность. Пусть компланарны. На этих векторах построим параллелограмм OABC.
Отсюда получим:
Векторы линейно зависимы, по определению. Доказано.
Слайд 10Теорема 5. В пространстве R3 любые 4 вектора являются
линейно зависимыми.
Док-во: аналогично доказ-ву Т.4 (достаточность), путем построения параллелепипеда
на 3-х некомпланарных векторах. Тогда 4-й вектор будет линейной комбинацией этих трех векторов, значит все 4 вектора линейно зависимые. Доказано.
Следствие. Любой вектор в трехмерном пространстве можно представить как линейную комбинацию базисных (некомпланарных) векторов, т.е. разложить по базису, причем такое разложение единственно.
Док-во: от противного. Пусть имеются два различных разложения вектора по одному базису . . Вычтем (1)-(2):
Из линейной независимости векторов базиса имеем , откуда . Значит, разложение единственно. Доказано.