Слайд 1Векторный и тензорный анализ
Алгебра тензоров над произвольным линейным пространством
Специальность 1-100
01 01 Ядерная и радиационная безопасность
2010-2011 уч. г.
Учреждение образования
«Международный
государственный экологический университет им. А.Д. Сахарова»
Факультет мониторинга окружающей среды
Слайд 2Конечномерные линейные пространства
Слайд 3Линейное пространство над полем
Буквы для обозначения линейного пространства –
латинские, прописные, рукописные, курсивом: A, B,…V, W
Элементы линейного пространства
называются векторами
Будем обозначать их буквами со стрелками:
Поле – числовое: Q, , либо
Будем обозначать их греческими буквами: ,…
Слайд 4Аксиомы линейного пространства
Линейное пространствоV над полем чисел –
множество элементов
, для которых установлены операции сложения и умножения на числа из , такие, что выполняются следующие аксиомы:
Слайд 5Линейные комбинации
Линейной комбинацией векторов
называется вектор
.
Числа называются коэффициентами линейной комбинации
Линейная комбинация называется тривиальной, если все числа
Слайд 6Линейная (не)зависимость
Векторы
называются линейно зависимыми, если
существует их нетривиальная линейная комбинация, равная нулевому вектору
Если такой нетривиальной линейной комбинации не существует, то векторы называются линейно независимыми
Слайд 7Размерность пространства. Базис
Если добавление любого вектора к семейству
линейно независимых векторов
приводит к семейству линейно зависимых векторов, то число n называется размерностью пространства. Обозначение: n = dim V.
Семейство называется базисом в пространстве V. В этом случае пишут V n.
Пространство называется конечномерным, если n – конечное натуральное число.
В тензорном анализе – конечномерные пространства
Слайд 8Разложение вектора по базису
Так как
при ненулевом и хотя бы одном ненулевом из i , , то
Таким образом возникает разложение вектора по базису
Координаты вектора
Запишем разложение вектора на составляющие
Слайд 9Правило Эйнштейна.
Метод коренных букв и индексов
Договоримся, что по повторяющимся
индексам сверху и снизу подразумевается суммирование в пределах заданного диапазона
изменения индекса – правило Эйнштейна
Если надо выделить отдельную составляющую вектора с номером i, будем писать
Такой способ записи называется методом коренных букв и индексов. Здесь a – коренная буква, а i – индекс. Его месторасположение (в данном случае вверху) также существенно
Слайд 10Единственность разложения в данном базисе
Допустим существует два различных разложения
и
для вектора в одном и том же базисе .
Тогда их разность
В силу линейной независимости векторов базиса отсюда вытекает т.е. .
Слайд 11Преобразование базисов
Вместо линейно независимого семейства
можно выбрать любое другое
линейно независимое семейство
Рассмотрим разложения
В этой записи точка под или
над индексом указывает место его расположения по отношению к соседнему индексу
Слайд 12Связывающие величины. Метод коренных букв и индексов (прод.)
Величины
– координаты нового базиса в старом
Величины
– координаты старого базиса в новом
Они называются связывающими величинами
Их роль – устанавливают связь между координатами вектора в разных базисах:
Попарно повторяющиеся (один сверху, один снизу) индексы называются немыми, неповторяющиеся индексы – явными
Правило: явные индексы в правой части равенства стоят на том же уровне, что и в левой его части
Слайд 13Как читать равенство
?
Необходимо придать конкретные значения индексам.
Запись
эквивалентна системе линейных уравнений
…
с коэффициентами .
– численно равно
Слайд 14Связь между связывающими величинами
где
символы Кронекера
Слайд 15Взаимно-однозначное соответствие V n и Kn
Разложение векторов по заданному
базису
есть построение взаимно однозначного соответствия: V n Kn,
где Kn = KK … K
Элементами Kn являются упорядоченные совокупности координат векторов в заданном базисе
Слайд 16Линейное пространство Kn
Введение операций сложения этих совокупностей:
и умножения на
числа из K
вводят Kn на структуру линейного пространства.
Тогда можно говорить
об изоморфизме V n и Kn а
Но этот изоморфизм – особый!
Слайд 17Координатный изоморфизм
Этот изоморфизм устанавливается только для каждого конкретного базиса
или
Он называется координатным изоморфизмом
и – вообще говоря, разные упорядоченные наборы чисел из Kn.
Иногда координатный изоморфизм называют арифметизацией линейного пространства V n.
Слайд 18Координатный изоморфизм – не тождество!
Но нельзя отождествлятьV n и
Kn, так как в зависимости от выбора базиса одному и
тому же вектору ставятся в соответствие, вообще говоря, различные упорядоченные наборы чисел из Kn.
Например, при преобразовании базиса отношение конкретных координат вектора не переходит в аналогичное отношение в базисе .
Задание: найти выражение для через координаты вектора в старом базисе
Слайд 19Запись функций от векторов
При составлении функций
, зависящих от векторов, необходимо подбирать выражения, не зависящие
от базиса.
Например, нельзя считать, что если в некотором базисе функция , то в любом другом базисе она остается функцией только первой координаты вектора:
Слайд 20Смысл индексных обозначений в общей записи функциональной зависимости
В то же
время наряду с обозначением функции от вектора
будет использоваться и запись
Здесь запись правой части означает не зависимость от конкретного , а от всей совокупности координат вектора в любом базисе, если не оговорено иное.
В частности, символом будем обозначать вектор в целом, если не оговорено иное.
Слайд 21Матричное представление векторов в Kn
Векторы в Kn можно представить в
виде вектор-столбца
Этот вектор-столбец содержит значения координат вектора
в базисе .
Будем обозначать вектор-столбец, составленный из координат того же вектора в базисе символом
Слайд 22Матричные образы базисных векторов
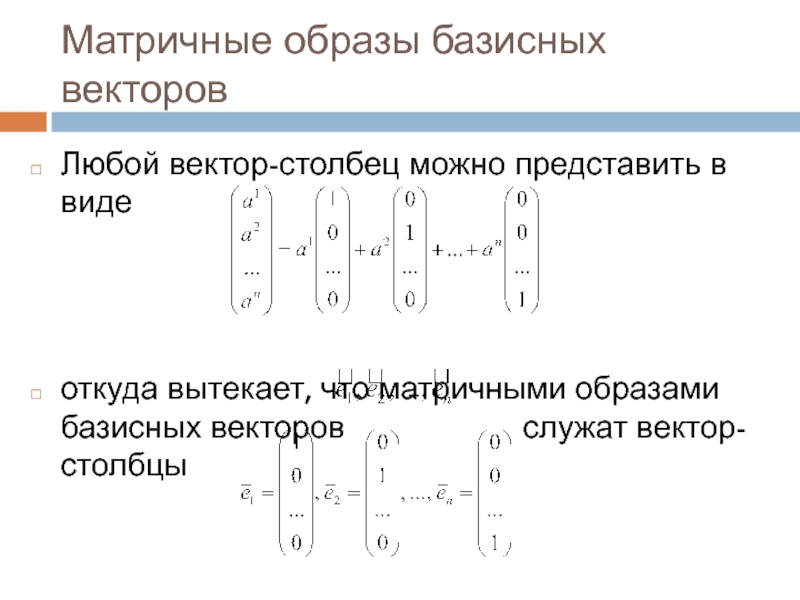
Любой вектор-столбец можно представить в виде
откуда
вытекает, что матричными образами базисных векторов
служат вектор-столбцы
Слайд 23Но:
Матричные образы базисных векторов
в этом же базисе будут
точно такие же!
А в базисе , как следует из системы
им соответствуют вектор-столбцы
Задача: Выписать вектор-столбцы, соответствующие матричному представлению базиса в базисе
Слайд 24Матричное представление связывающих коэффициентов
Связывающие коэффициенты
можно перечислить в виде матрицы
составленной по правилу: первый индекс
независимо от уровня нумерует строки, а второй – столбцы
Слайд 25Матричное представление связывающих коэффициентов
По тому же принципу: первый индекс нумерует
строки, второй столбцы, запишем перечень связывающих коэффициентов
в виде матрицы
Слайд 26Матричное представление
В этих обозначениях систему уравнений, связывающих координаты
вектора в базисе
с его же координатами в базисе можно записать в матричном виде
что эквивалентно записи
правую часть которой можно читать как произведение строки с номером i на столбец, составленный из координат .
Слайд 27Особенность матричного представления
В то же время, обратное преобразование
(*)
не эквивалентно записи , так как правую часть ее надо читать, как произведение столбца с номером i на строку, составленную из координат вектора .
Но если (*) протранспонировать, то соотношение
можно прочитать в духе формулы
Слайд 28Особенность матричного представления
Отсюда видно, что матрица связывающих коэффициентов
связана с матрицей Р соотношением
(**)
Записывая соотношение в индексной форме, для сохранения матричного правила умножения «строка на столбец» элементы матрицы Р–1 придется обозначить символами .
Но в то же время запись условия (**) в индексной форме имеет вид , так как операция транспонирования приводит к перестановке индексов у элементов матрицы . Но тогда придется не отличать коренные буквы Р–1 и Р, что приведет к неоднозначности применения метода коренных букв и индексов
Слайд 29Особенность матричного представления
В условленных ранее обозначениях компонент матриц Р и
соотношение между их компонентами
эквивалентно следующей простой матричной форме
записи
РР–1 = Р–1Р = E
где E – единичная матрица
Слайд 30Выводы
Матричное представление менее информативно, чем индексное представление. Но его удобнее
использовать при расчетах в конкретном базисе
Необходимо отличать векторы из пространстваV
n и векторы из пространства Kn :
одному и тому же вектору отвечает бесконечное множество векторов , составленных из координат вектора во всех возможных базисах пространстваV n.
Слайд 31Линейное пространство, сопряженное к данному
Слайд 32Функционалы
Отображение V n K, ставящее в соответствие любому
вектору изV n некоторое число из K, называется
функционалом над линейным пространством V n.
Функционал первоначально будем обозначать символом
Слайд 33Линейные функционалы
Функционал называется линейным, если для
любых векторов
и любого числа из K выполняются следующие условия:
,
Множество всех функционалов над линейным пространством V n образует линейное пространство над полем чисел K (доказать!).
Слайд 34Линейное пространство, сопряженное к V n
Это пространство называется линейным
пространством, сопряженным к V n и обозначается V
n.
Его элементами являются все возможные функционалы, заданные над линейным пространством V n.
Можно показать, что dim V n = n (см. ниже).
Слайд 35Ковекторы
Линейные функционалы как элементы линейного пространства будем обозначать коренной буквой
со стрелкой снизу:
Они называются ковекторами пространства V n.
Часто векторы
из V n называются контравариантными векторами, а векторы из V n – ковариантными векторами.
Слайд 36Вычисление значений линейных функционалов
Выражение является числом
из K для каждого отдельного вектора
и каждого отдельного ковектора .
Разложим вектор по базису вV n:
В соответствии со свойствами линейного функционала число можно представить в виде
Слайд 37Базисы в сопряженном пространстве
Так как V n содержит все
возможные линейные функционалы, то для каждого базиса
вV n в V n существует n линейно независимых функционалов
, для которых
Они составляют базис в V n.
Если функционал представить в виде разложения
То можно получить отсюда, что числа ai находятся по правилу
Слайд 38Вычисление линейных функционалов в заданном базисе. Свертка
Тогда значение функционала
на данном векторе
будет вычисляться следующим образом
Базисы и называются взаимно сопряженными.
Выражение называется сверткой (от немецкого – Faltung) вектора и ковектора .
Числа ai имеют смысл координат ковектора в базисе
Слайд 39Линейная форма
Однородная линейная комбинация координат вектора
в произвольном базисе
называется линейной формой на векторах
, или 1-формой
Она представляет собой свертку вектора с ковектором .
Слайд 40Координатный изоморфизм для ковекторов
Поскольку ai – числа из K, то
разложение ковектора по базису
представляет собой координатный изоморфизм V n Kn,
При этом Kn выступает как линейное пространство.
Поскольку базисы и принадле-жат разным пространствам и не тождественны друг другу, то из факта существования двух координат-ных изоморфизмов V n Kn иV n Kn не следует существование изоморфизма между сопряженными друг другу пространствами V n и V n
Слайд 41Эффективность обозначений с разностоящими индексами
В частности, это значит, что обозначения
ai и ai относятся к различным векторам, принадлежащим разным пространствам,
не смотря на одинаковую коренную букву .
Таким образом, индексные обозначения ai и ai, понимаемые как обозначения вектора и ковектора вообще, независимо от выбора базиса, однозначно определяют вектор и ковектор как таковые и эквивалентны прямым обозначениям и соответственно.
Слайд 42Преобразования базисов в пространствах V n и V
n
Пусть базисы
и связаны в V n разложениями
Тогда для соответствующих сопряженных базисов и в V n из определений и вытекает, что
т.е. координаты векторов в базисе
имеют смысл координат ковекторов
в базисе .
Слайд 43Преобразование координат ковекторов. Инвариантность свертки
Для координат ковекторов из разложений
следует, что
Из
определения свертки
вытекает ее инвариантность относительно преобразований базиса
Величины, не меняющиеся при преобразованиях координат, называются скалярами
Слайд 44Контравариантные и ковариантные векторы
Векторы, координаты которых при преобразовании базиса преобразуются
по закону
называются контравариантными векторами,
а векторы, координаты которых преобразуются по закону
называются
ковариантными векторами.
Слайд 45Матричная интерпретация преобразований координат ковекторов
Координаты ковектора можно собрать
в вектор-столбец
аналогично вектор-столбцу, который может быть поставлен в соответствие
контравариантному вектору. Тогда в соответствии с индексной формой записи и правилами перемножения матриц
в отличие от связи между вектор-столбцами кон-травариантного вектора в разных базисах:
Слайд 46Матричная интерпретация свертки
Свертку
контравариантного вектора с ковариантным вектором
можно представить в матричной записи как произведение строки на столбец :
Слайд 47Вектор – не столбец, а ковектор – не строка!
Поэтому нельзя
считать, что в заданном базисе линейное пространство контравариантных векторов изоморфно
линейному пространству вектор-столбцов, составленных из координат этих векторов, а линейное пространство ковариантных векторов изоморфно линейному пространству вектор-строк, составленных из координат ковекторов в базисе, сопряженном базису, в котором получено разложение ковариантных векторов.
Оба матричных образа в равной мере применимы для частного представления тех и других
Слайд 48РавноправиеV n иV n
Можно было бы рассматривать
векторы изV n как функционалы на ковекторах изV
n, пользуясь определением
Поэтому можно было бы писать выражение для свертки ковариантного и контравариантного векторов в более простом виде
Слайд 50Определение линейного оператора
Линейным оператором называется отображение пространства U
m в пространствоV n над одним и тем же полем
чисел K, обозначаемое , при котором каждому вектору ставится в соответствие некоторый вектор и при этом выполняются следующие условия:
для
для
Пространство U m называется областью определения линейного оператора , а множество всех векто- ров – областью образов линейного оператора .
Слайд 51Сложение линейных операторов
Рассмотрим два оператора
и
Суммой операторов и называется оператор, обозначаемый , такой, что для любого
Оператор называется нулевым оператором, если область его образов – нулевой вектор:
Слайд 52Произведение линейных операторов
ПустьU m, V n,W p –
линейные пространства размерности m, n и p соответственно над одним
и тем же полем чисел K.
Пусть заданы линейные операторы и
Произведением операторов и называется оператор, обозначаемый , ставящий в соответствие векторам из U m векторы изW p.
Порядок следования операторов в произведении существен
Слайд 53Координатное представление операторов
Пусть – линейный оператор:
Рассмотрим базис
в пространстве U m и базис в пространствеV n
Рассмотрим векторы и
Разложим эти векторы по указанным базисам:
Тогда из линейности оператора вытекает
Слайд 54Координатное представление операторов
Векторы
, поэтому их можно разложить по базису
где
– коэффициенты разложения векторов по базису . Они однозначно определяют линейный оператор в базисах , и называются координатами оператора в указанных базисах.
Слайд 55Преобразование координат оператора при преобразованиях базисов
Пусть
и
– некоторые новые базисы в U m и V n соответственно.
Выпишем следующие разложения базисов в U m и V n :
Тогда координаты оператора в новых базисах будут связаны с его координатами в старых базисах соотношениями
(^)
Задача: найти все возможные способы вывода (^)
Слайд 56Координатное представление произведения операторов
Рассмотрим линейные пространстваU m,V n,
W p размерности m, n и p соответственно над
одним и тем же полем чисел K.
Выберем в U m,V n,W p базисы
соответственно.
Тогда произведение операторов и будет однозначно задаваться его координатами
Слайд 57Матричное представление операторов
Координатный изоморфизм ставит во взаимно-однозначное соответствие любому линейному
оператору его координаты
в заданных базисах и .
Если договориться, что первый индекс, нумерующий базисные векторы в пространстве образов оператора, будет нумеровать строки, а второй индекс, нумерующий базисные векторы в области определения оператора – столбцы, то оператор можно представить в виде матрицы размера nxm
Слайд 58Матричное представление операторов
В развернутой форме
На матричном языке произведение операторов рассматривается
как произведение соответствующих матриц
Слайд 60Автоморфизм
Оператор
называется автоморфизмом, если U m =V
n, m=n.
Произведение автоморфизмов и является автоморфизмом.
Автоморфизм называется единичным, если
Обратным автоморфизмом называется оператор , такой, что
Оператор, имеющий на V n обратный оператор, называется невырожденным.
Слайд 61Группа GL(n)
Множество всех невырожденных линейных автоморфизмов на V
n образует мультиплика-тивную группу GL(n), называемую общей линейной группой автоморфизмов
наV n .
Слайд 62Определение группы
Группой G называется множество элементов, f, g, h, …, для которых задан
некоторый закон композиции (если f G, g G , то композиция gf G и
элемент gf определен однозначно), удовлетворяющий следующим условиям:
1 (hg)f = h(gf) для любых h, g, f G;
2 существует единичный элемент e, для которого ef = fe = f для любого f G;
3 для любого f существует обратный элемент f–1, определяемый условиями:
f–1f = ff–1= e.
Группа называется коммутативной, или абелевой, если для любой пары f и g G fg = gf.
Слайд 63Коммутатор операторов
Для любых двух автоморфизмов и
автоморфизм
называется коммутатором операторов и
Операторы, коммутатор которых
равен нулю, называются коммутирующими (перестановочными) операторами
Задача. Показать, что
1.и
2. (Тождество Якоби)
Группа, умножение элементов в которой обладает свойствами 1,2, называется группой Ли
Слайд 64Идемпотентные автоморфизмы
Автоморфизм называется идемпотентным автоморфизмом на V
n, если
Все идемпотентные автоморфизмы не вырождены. Причем
Слайд 65Нильпотентные автоморфизмы
Автоморфизм называется нильпотентным, если найдется такое натуральное
p, для которого
Если при этом
, то число p называется индексом нильпотентности оператора .
Слайд 66Проективные операторы
Проективным оператором называется автоморфизм, для которого
Проективный оператор ставит в
соответствие любому вектору
вектор , который не меняется под действием оператора .
Любому проективному оператору можно поставить в соответствие проективный оператор
Свойство операторов и :
Области образов операторов и не пересекаются.
Слайд 67Связь между проективными и идемпотентными операторами
Если оператор является
идемпотентным: ,
то оператор
является проективным оператором, так как
Оператор
также будет проективным, если идемпотентен, при некотором а. Найти а
Слайд 68Координатное и матричное представление автоморфизмов
Координаты линейного автоморфизма
могут быть записаны относительно одного базиса
и собраны
в квадратную матрицу размера nxn
Слайд 69Координатное представление некоторых автоморфизмов
Координатами единичного оператора в любом
базисе являются символы Кронекера
а в матричном представлении он представляется единичной
матрицей:
Координаты нулевого оператора в любом базисе равны нулю и составляют нулевую матрицу.
Это два простейших примера т.н. индифферентных операторов
Слайд 70Координатное задание обратного оператора
Для невырожденного оператора соотношение
можно
переписать в виде
Производя разложение векторов
и в некотором базисе , получим
а индексная запись соотношения будет выглядеть так:
Слайд 71Линейные автоморфизмы в сопряженном пространстве
Как будет выглядеть действие линейного автомор-физма
в пространстве V n, сопряженном кV
n, если задан наV n?
А как зададим! Но есть всего 2 возможности
1. Для любых вектора и ковектора значение на образе вектора равно
Слайд 72Линейные автоморфизмы в сопряженном пространстве
Поэтому можно представить, что автоморфизм
, действующий на векторы пространстваV n слева направо,
действует на ковекторы сопряженного пространстваV n справа налево, а именно:
При таком представлении действия оператора на сопряженном пространствеV n в выражении скобки можно опустить
Слайд 73Матричная интерпретация в заданном базисе
И это выражение в любом наперед
заданном базисе можно трактовать непосредственно в матричной форме:
Слайд 74Правые автоморфизмы на V n
2. Правым линейным автоморфизмом
наV n называ-ется линейный оператор , ставящий в
соответствие любому вектору вектор , так что
1. для
2. для
Операторы, действующие «традиционным способом» слева направо, будем называть левыми операторами.
Что же в этом определении отличного от определения левого линейного оператора?
Слайд 75Координатное представление правых автоморфизмов
В некотором базисе
правый автоморфизм можно представить в виде
где координаты – однозначно определяют действие оператора на векторы справа.
Перенос его действия на ковекторы изV n приводит к левому действию оператора на сопряженном пространствеV n
Слайд 76В матричном виде
Если обозначить символом матрицу коэффициен-тов
, определяющих правое действие оператора на векторы пространстваV
n и левое действие – на ковекторы из V n , то
Слайд 77Свертка образов автоморфизма, левого наV n и правого наV
n
Если теперь рассмотреть свертку образа
вектора в с соответствующим образом ковектора в , то окажется, что свертка, вообще говоря, не инвариантна относительно автоморфизмов пространства:
Инвариантность свертки будет иметь место лишь в случае идемпотентных автоморфизмов, для которых
Слайд 78Свертка левых образов одного и того же автоморфизма
Если же
рассмотреть свертку левого образа вектора
с левым образом ковектора у , то получим выражение
Свертка таких образов будет инвариантна относите-льно линейного автоморфизма: , если
(*^)
а на языке соответствующих матриц
Слайд 79Свертка правых образов одного и того же автоморфизма
Аналогично для
правых образов
Условие инвариантности
дает
(*^)
что эквивалентно тому же матричному условию
Слайд 80Преобразование координат левых автоморфизмов при преобразовании базиса
Координаты
левого линейного автоморфизма могут быть записаны относительно одного
базиса
и собраны в квадратную матрицу размера nxn
При преобразовании базиса они преобразуются по линейному однородному закону
Слайд 81Преобразование координат левых автоморфизмов при преобразовании базиса
Можно, конечно, «забыть» преобразовать
один из индексов, относя их к разным базисам и вводя
коор-динаты оператора в смешанном виде
В этих случаях суть дела не меняется: оператор по-прежнему задает некоторое линейное отображение пространстваV n в себя, только числа, характери-зующие его, отнесены к различным базисам по каждому из индексов.
Вопрос: Являются ли связывающие коэффициенты Pij координатами некоторого левого линейного оператора?
Слайд 82Преобразование координат левых автоморфизмов при преобразовании базиса
Ответ: Да. Связывающие коэффициенты
Pij являются смешанными координатами единичного оператора, ибо по определению
Точно так
же связывающие коэффициенты Pj i являются смешанными координатами единичного оператора
Слайд 83Преобразование координат правых автоморфизмов при преобразовании базиса
Аналогично при преобразовании
базиса вV n преоб-разование координат правого
автоморфизма на V n происходит по линейному однородному закону
В употреблении также могут оказаться смешанные координаты правого оператора
Отсюда также можно установить, что связывающие коэффициенты являются смешанными координа-тами единичного оператора в данных базисах
Слайд 84Связывающие коэффициенты – не линейные автоморфизмы!
Являются координатами базисных векторов
в базисе пространства V
n,
либо координатами ба-зисных векторов в базисе в простран-ствеV n
Являются координатами образов в базисе в пространстваV n ,
либо координатами образов в базисе в в пространстве V n
Связывающие коэффициенты
Pi j
Координаты автоморфизмов
Li j
Слайд 85Левые линейные отображения V n наV n
Рассмотрим
теперь линейный оператор , ставящий в соответствие
каждому вектору некоторый ковектор :
Разложив вектор в некотором базисе , а вектор – в соответствующем сопряженном базисе м , в силу линейности оператора будем иметь
Обозначим
Слайд 86Левые линейные отображенияV n наV n и V
n наV n
Тогда
(*^)
Коэффициенты
Lij однозначно задают действие линейного оператора в некоторых сопряженных друг к другу базисах и .
Соответственно, для некоторого линейного опера-тора : уравнения
в некоторых базисах и запишутся в виде
(^*)
Слайд 87Правые линейные отображенияV n наV n и V
n наV n
Точно так же можно определить действие
этих же операторов справа:
При этом векторные уравнения и записываются в координатном виде следующим образом
Задача: Записать эти соотношения а также соотноше-ния (*^) и (^*) в матричном виде.
Слайд 88Законы преобразования Lij и Lij
При переходе к новому базису
вV n
и соответствующему сопряженному базису вV n
координаты
операторов и преобразуются по линейному однородному закону (вывести!)
Получить аналогичные правила преобразования для координат оператора
Слайд 89Итого:
Прямая запись
Координатная запись
Матричная запись
Свертка. Для
Левые операторы
Правые операторы
Слайд 90Итого:
Прямая запись
Координатная запись
Матричная запись
Свертка. Для
Левые операторы
Правые операторы
Слайд 91Итого:
Прямая запись
Координатная запись
Матричная запись
Свертка. Для
Левые операторы
Правые операторы
Слайд 92Итого:
Прямая запись
Координатная запись
Матричная запись
Свертка. Для
Левые операторы
Правые операторы
Слайд 93Упражнение – варианты сверток
1.
2.
3.
4.
Запишите остальные допустимые свертки образов. Охарактеризуйте
операторы, оставляющие свертки инвариантными.
Свертка правого и левого образов
Свертка одноименных
образов
Слайд 94Определения и алгебраические операции
Общее понятие о тензорах
Слайд 951. Билинейный функционал на V n
Билинейным функционалом
на векторах и
изV n называется линейное по обоим аргументам отображение , такое, что для любого числа и для любых векторов
выполняются следующие условия:
1
2
3
4
Билинейные функционалы на V n образуют линейное пространство T2(n) над полем K.
Слайд 961. Билинейный функционал наV n
Пусть
– некоторый базис в V n
Обозначим значения билинейного функционала и на базисных векторах символом
Числа Bij называются коэффициентами функционала B в базисе . Они определены однозначно для каждого функционала.
Тогда, пользуясь свойствами линейности функционала и по обоим аргументам, на основе разложений и и получим
– билинейная форма
Слайд 971. Билинейный функционал наV n
Переход к другому базису
не должен влиять на значение величины . Поэтому совокупность координат преобразуется в совокупность координат и по линейному однородному закону
(*)
Совокупность координат билинейной формы образует тензор типа (0,2) или ковариантный тензор валентности 2. Число индексов называется валентностью тензора.
Слайд 981. Билинейные функционалы на V n
Аналогично можно построить
пространство T2(n) билинейных функционалов наV n как множество всех
билинейных отображений вида
Такой билинейный функционал в некотором базисе и однозначно описывается совокупностью координат
Для любых ковекторов значение такого били-нейного функционала представляет собой билинейную форму
Слайд 991. Билинейные функционалы на V n
Преобразование базиса
вV
n должно оставлять неизменным значение функционала
Поэтому коэффициенты билинейной формы Bij должны преобразовываться по закону
(**)
Величины, совокупность координат которых преобразуется по линейному однородному закону вида (**), называются тензорами типа (2,0) или контравариантными тензорами валентности 2.
Слайд 1001. Смешанные билинейные формы
Упражнение:
Сформулируйте определение смешанных билинейных форм
Тензоры типа (1,1),
или смешанные тензоры второй валентности
Задача: покажите, что всевозможные свертки образа
линейного оператора с сопряженным ему вектором являются билинейными формами
Слайд 1011. Векторы и скаляры как тензоры
Контравариантные векторы называются тензорами типа
(1,0)
Ковариантные векторы называются тензорами типа (0,1)
В этом же духе скаляры
– тензоры типа (0,0)
Слайд 1022. Тензорное произведение векторов
Тензорным произведением векторов и
называ-ется выражение, обозначаемое как
для которого определены все свойства билинейности
1 – 4 и, кроме того, установлены следующие прави-ла действия на ковекторы (свертки с ковекторами):
Слайд 1032. Диадное произведение
Разложив векторы и в
базисе
, представим тензорное произведение в виде
(^)
Оно имеет смысл линейной комбинации базисных векторов с коэффициентами xiyj.
Выражение (^) называют также диадным произведением векторов.
Представляющая его матрица коэффициентов (xiyj) называется матрицей-диадой.
В общем случае
Слайд 1042. Прямое представление контравариантного тензора валентности 2
В этих обозначениях контравариантный
тензор Bij можно представить в виде
где
можно рассматривать как базис в пространстве T2(n).
Упражнение: Показать, что из свойств тензорного произведения векторов вытекает следующий результат
Слайд 1052. Диадное произведение ковекторов
Для ковекторов и
также можно ввести понятие тензорного произведения
которое в некотором базисе
представится в виде разложения
и называется диадным произведением ковекторов.
В общем случае
Слайд 1062. Прямое представление ковариантного тензора валентности 2
Точно так же ковариантный
тензор Bij можно представить в виде
где
можно рассматривать как базис в пространстве T2(n).
Упражнение: Показать, что
Слайд 1072. Прямое представление смешанных тензоров валентности 2
Существует два типа линейных
пространств смешанных тензоров, которые будем обозначать
символом T11(n) для тензоров
вида
с базисом
и символом T11(n) для тензоров вида
с базисом .
В отличие от T2(n) и T2(n), в T11 (n) и T11 (n) существует еди-ничный тензор, который можно обозначить одинаковой буквой, не внося путаницы:
Слайд 1082. Как лучше обозначить тензоры второй валентности?
Векторы
Тензоры второй валентности
Индексная форма
записи
Прямая форма записи
Слайд 1092. Как лучше обозначить тензоры второй валентности?
В индексной записи все
однозначно, а в прямой записи возникает проблема идентификации типа тензора.
Поэтому необходимо либо явно выписывать тензор в разложении по некоторому тензорному произведению базисных векторов, либо использовать индексные обозначения, подразумевая под ними, когда это необходимо, прямые образы тензоров.
В прямой записи тензора в разложении по тензорному произведению базисных векторов еще не содержится закона преобразования его координат. Необходимо постулировать дополнительно неизменность таким образом обозначенной величины при преобразовании базиса.
Слайд 1103. Транспонирование тензоров второй валентности
Для тензорного произведения векторов может быть
введена операция транспонирования, определяемая как линейный оператор, ставящий в соответствие
некоторой диаде диаду с противоположным порядком следования векторов:
Слайд 1113. Транспонирование тензоров второй валентности
Транспонирование является линейным автоморфиз-мом на T2(n)
и T2(n) и линейным взаимно однознач-ным отображением T11(n) на T11(n)
и наоборот.
Задача. Применяя операцию транспонирования к произвольным тензорам второй валентности, пользуясь линейностью этой операции, получить правила действия транспонирования на координаты этих тензоров:
BТij = Bji, BТij = Bji, BТij = Bji.
Слайд 1123. Симметричные и антисимметричные тензоры второй валентности
Тензор второй валентности типа
(2,0), либо типа (0,2) на-зывается симметричным, если для всех его
координат вы-полняется соотношение
Bji =Bij , Bji = Bij
Тензор второй валентности типа (2,0), либо типа (0,2) на-зывается антисимметричным, если для всех его коорди-нат выполняется соотношение
Bji =–Bij , Bji = –Bij.
Слайд 1133. Симметризация тензоров второй валентности
Симметризацией или симметрированием тензора второй валентности
называется оператор, ставящий в соответствие исходному тензору тензор,
где
Слайд 1143. Альтернирование тензоров второй валентности
Альтернацией или альтернированием тензора второй валентности
называется операция, ставящая в соответствие исходному тензору тензор,
где
Слайд 1153. Симметричная и антисимметричная части тензора
Задача. Показать, что для любого
тензора второй валентности типа (2,0) или (0,2)
или, на языке координат
тензора
B(ij) – симметричная часть тензора Bij,
B[ij] – антисимметричная часть тензора Bij.
Замечание. Понятие симметрирования и альтернации для смешанных тензоров второй валентности смысла не имеют, так как тензоры и и относятся к разным пространствам T11(n) и T11(n) соответственно.
Слайд 1163. Еще задачи
3.1. Показать, что, если тензор Sij симметричен, то
Sij = S(ij).
3.2.
Показать, что, если тензор Aij антисимметричен, то
Aij = A[ij].
3.3. Показать, что диагональные координаты любого антисимметричного тензора равны нулю: Aii = 0
3.4. Показать, что из n2 координат симметричного тен-зора только n(n+1)/2 оказываются линейно незави-симыми координатами, а антисимметричный тензор определяется n(n–1)/2 независимыми координатами
Слайд 1173. Внешнее произведение
Антисимметричный ковариантный тензор Aij = –Aji можно представить
в виде
где
называется внешним произведением базисных векторов.
Слайд 1183. Внешняя форма второго порядка
Антисимметричный ковариантный тензор второй валентности называется
внешней формой второй степени или внешней 2-формой.
Не запрещено называть контравариантные
антисимметричные тензоры также внешними 2-формами. Это будут билинейные антисимметрич-ные функционалы на V n.
Их представляют в виде
Слайд 1193. Бивекторы
Внешнее произведение векторов и изV
n,
называется бивектором или простым антисимметричным тензором. Векторы
и называются делителями бивектора.
Это определение может быть распространено и на ковариантные векторы и изV n:
Упражнение. Найти число всех возможных линейно независимых бивекторов наV n (наV n)
Слайд 1203. Колинеарность векторов
Векторы и называются колинеарными,
если существует такое число , что
Критерий колинеарности
Векторы и
колинеарны тогда и только тогда, когда их внешнее произведение равно нулю
Примечание: здесь 0 – нулевой антисимметричный тензор валентности 2.
Слайд 1214. Свертка произвольного тензора второй валентности и вектора
Для произвольного тензора
можно говорить о левой и правой свертке с соответствующим (ко)вектором
Задание. Дайте интерпретацию выписанным выражениям с точки зрения теории операторов
Слайд 1224. Ранг ковариантного тензора второй валентности
Обозначим для краткости одной буквой
B ковариантный тензор
Рассмотрим этот тензор как оператор, переводящий векторы
изV n в ковекторы изV n либо по правилу левого умножения (левой свертки), либо по правилу правого умножения (свертки)
Множество всех возможных правых и левых образов оператора B образует подпространствоR (Bij) в сопряженном пространстве V n. Эти ковекторы называются ковекторами, ассоциирован-ными с тензором B.
R (Bij) называется ранговым пространством тензора Bij.
Размерность этого подпространства r = dimR (Bij) называется рангом тензора Bij.
Слайд 1234. Ранг произвольного тензора второй валентности
Данное выше определение ранга ковариантного
тензора второй валентности mutatis mutandis переносится на контравариантные и смешанные
тензоры второй валентности.
Упражнение. Сформулировать определения ранга
1) контравариантного тензора второй валентности
2) смешанного тензора
3) смешанного тензора
Установите сходство и различия в определениях. Нужно ли говорить о разных понятиях ранга для смешанного тензора по каждому из индексов?
Слайд 1244. Теорема о ранге тензора второй валентности
Ковариантный тензор B второй
валентности ранга r может быть представлен в виде разложения по
тензорным произведениям пар r линейно независимых базисных векторов изR (Bij)
причем в этом разложении суммирование идет по каждому из индексов от 1 до r.
Ранг тензора характеризует его инвариантные свойства, не зависящие от выбора базиса.
Ранг тензора валентности 2 равен рангу представляющей его матрицы
Слайд 1254. Разложение антисимметричного тензора второй валентности на листы
Антисимметричный тензор второй
валентности называется простым, или однолистным, если он пропорционален некоторому бивектору.
Разложение
произвольного антисимметричного тензора второй валентности по бивекторам, составленным из базисных векторов опорного векторного пространства, можно представить как разложение на листы
где , а r – ранг тензора. Минимальное чи-сло листов p, на которые может быть разложен антисимметричный тензор, определяется его свойствами и размерностью пространства.
Упражнение. Показать, что при n = 2,3 все антисимметричные тензоры валентности 2 – однолистные
Слайд 1264. Значение билинейного функционала, как свертка по двум векторам
Билинейная форма
может
рассматриваться как свертка:
Аналогично
Упражнение. Записать значения смешанных функционалов как свертку
с векторами и ковекторами.
Слайд 1274. Свертки диад
С помощью понятия свертки можно ввести понятие произведения
диад, аналогичное произведению матриц, а именно
При таком перемножении свертка диад
(ко/контра)вариантных и (контра/ко)вариантных векторов превращается в смешанные диады.
Упражнение: Построить остальные возможные виды диад и их свертки
Слайд 1284. Свертки тензоров второй валентности друг с другом
Определение произведения со
сверткой, сформули-рованное выше для диад, в силу линейности тензор-ного произведения
переносится на произвольные тензоры:
Упражнение. Выписать остальные возможные варианты сверток для всех типов тензоров второй валентности
Слайд 1294. След смешанного тензора второй валентности
Рассмотрим смешанную диаду
из T11 (n).
Назовем следом диады линейный
функционал, ставящий в соответствие диаде свертку составляющих ее векторов
Очевидно, что
Из линейности следа вытекает, что
Слайд 1304. След смешанного тензора второй валентности
Аналогично определяется понятие следа тензора
из T11 (n):
Применяя операцию взятия следа к диадному произведению
векторов, в частности, будем иметь
Но в общем случае
Показать, что
Слайд 1314. Полная свертка произведения тензоров второй валентности
Если вычислить след от
произведений
то можно получить скаляры, являющиеся свертками тензоров второй валентности по
двум индексам, или полными свертками
Слайд 1324. Полная свертка симметричного и антисимметричного тензоров второй валентности
Задача. Показать,
что полная свертка любого симметричного, Sij = Sji, и произвольного
антисимметричного , Aij = – Aji, тензоров второй валентности тождественно равна нулю:
SijAij = 0.
Другое определение антисимметричного тензора: ковариантный тензор второй валентности называется антисимметричным, если для любого вектора выполняется условие
Слайд 1335. А если тензорно перемножить три вектора?
Из любых трех векторов
вV
n можно построить трилинейное отображение (триаду), ставящее в соответствие любой упорядоченной тройке ковекторов изV n число (полная свертка)
В некотором базисе
Слайд 1345. Различные линейные пространства тензоров третьей валентности
Всего существует 8 различных
произведений
Следовательно, всего существует 8 типов линейных пространств тензоров валентности 3
над линейным пространствомV n и сопряженным к нему линейным пространствомV n:
T3(n) – линейное пространство контравариантных тензоров 3-й валентности (тензоры типа (3,0));
T3(n) – линейное пространство ковариантных тензоров 3-й валентности (тензоры типа (0,3));
T12(n), T111(n), T21(n), T12(n), T111 (n), T21(n) – линейные пространства различных смешанных тензоров третьей валентности (тензоры типа (1,2) или (2,1)).
Слайд 1355. Координатное представление тензоров третьей валентности
Тензоры 3 валентности различных типов
могут быть представлены в виде разложений по базисам в соответствующих
пространствах, а эти базисы могут быть представлены в виде тензорных произведений базисных векторов изV n иV n:
Слайд 1365. Законы преобразования координат тензоров третьей валентности
При связанных друг с
другом преобразованиях базиса в V n иV n
Задача:
выписать законы преобразования координат остальных тензоров третьей валентности
Слайд 1375. Транспонирование тензоров третьей валентности
Операцию транспонирования, введенную выше для тензоров
второй валентности, можно ввести и для тензоров третьей валентности следующим
образом:
Слайд 1385. Циклическая и антициклическая перестановки
Циклические перестановки 3 векторов в тройном
тензорном произведении
Антициклические перестановки получаются путем перестановки одной из пар векторов
в каждой из циклических перестановок.
Слайд 1395. Полное симметрирование и антисимметрование триады
Определим операцию полного симметрирования триады
по трем векторам следующим образом:
Аналогично определим операцию полного антисиммет-рирования триады
по трем векторам:
(1,2,3) – перестановка номеров векторов в произведении по порядку их следования, = 1, – четность перестановки
Слайд 1405. Полное симметрирование тензора третьей валентности
Рассмотрим произвольный ковариантный тензор третьей
валентности
Полной симметричной частью этого тензора по трем векторам тензорного
произведения называется тензор
где
Слайд 1415. Полная антисимметризация тензора третьей валентности
Рассмотрим произвольный ковариантный тензор третьей
валентности
Полной антисимметричной частью этого тензора по трем векторам тензорного
произведения называет-ся тензор
где
Слайд 1425. Выражение через симметричную и антисимметричную части
Отметим, что
Поэтому тензор третьей
валентности в общем случае не раскладывается на полные симметричную и
антисимметричную части.
Задача. Найти все способы выражения величины Bijk через ее полные и частичные (по двум индексам) симметричную и антисимметричную части
Слайд 1435. Свертки тензоров третьей валентности с векторами
Что мы можем записать
Однако
свертка со средним вектором в этих обозначе-ниях уже не поддается
аналогичной записи без при-менения операции транспонирования, например,
Слайд 1445. Индексная форма – проще всего!
Те же результаты гораздо проще
записываются в индексной форме
Bijkak, Bijkai, Bijkaj
без употребления явной записи базиса
с линейном пространстве, которому эти объекты принадлежат.
При этом не требуется прибегать к операции транспонирования – все выглядит естественно.
Слайд 1455. Ранговое подпространство тензора третьей валентности
Свертки с всевозможными диадами ковекторов
Bijkajbk,
Bijkaibk, Bijkaibj
(*:^)
образуют линейное подпространство вV n , называ-емое ранговым пространством R (Bijk) тензора Bijk.
Размерность рангового подпространства
r = dimR (Bijk)
называется рангом тензора Bijk.
Аналогичные определения mutatis mutandis могут быть сформулированы для других типов тензоров третьей валентности (сформулируйте!)
Слайд 1465. Свертки тензоров третьей валентности с тензорами второй валентности
Прямая запись
произведений тензоров третьей и второй валентностей со сверткой по близ(или
не близ)лежащим индексам также громоздка, например,
В то время как в индексной форме записи
BijkDkm, DliBijk, и т.п.
Слайд 1476. Общее определение тензора
Тензором типа (p,q) над линейным пространством V
n называется элемент некоторого линейного пространства, образованного путем тензорного
произведения p линейных пространствV n и q линейных пространствV n, одним из способов, например,
такой, что при любом преобразовании базиса в V n иV n его координаты преобразуются по линейному однородному закону
Слайд 1486. Валентность тензора
Например
Порядок следования пространствV n иV n
существен.
Число p называется контравариантной валентностью тензора, а число q –
ковариантной валентностью тензора; сумма p + q называется полной валентностью, или просто валентностью тензора.
Слайд 1496. Полилинейные формы
Любой ковариантный тензор валентности q
определяет полилинейную форму на
векторах изV n:
Аналогичное понятие полилинейной формы на ковекторах изV
n можно ввести с помощью контравариантных тензоров.
Упражнение. Сформулировать определение полилинейной формы на ковекторах
Слайд 1507. Допустимые операции над тензорами
Операции, описываемые аксиомами линейного пространства: сложение
тензоров, принадлежащих одному тензорному пространству, умножение тензора на число и
свойства коммутативности и ассоциативности этих операций, а также их дистрибутивности по отношению друг к другу
Инверсия (перестановка, в случае двух индексов – транспонирование) – образование новых тензоров из исходных путем перестановки индексов, например,
Cijk = Bkji
Слайд 1517. Тензорное умножение и свертка
Тензорным произведением тензоров типа (p1,q1) и
(p2,q2) называется тензор типа (p1+p2,q1+ q2), например,
Aijkl =CilBkj
Порядок следования
индексов в произведении может быть выбран произвольно с учетом операции инверсии.
Сверткой тензора по контравариантному и ковариантному индексам называется сумма вида
Ai…j…j…kl
Каждая свертка уменьшает валентность тензора на 2.
Слайд 1527. Ранг тензора
Всевозможные свертки тензора с векторами изV n
и ковекторами изV n по всем индексам, кроме одного
, приводят к понятию контравариантного,
и ковариантного,
ранговых подпространств тензора по контра-вариантному индексу is, либо по ковариантному индексу js соответственно.
Размерности этих подпространств и определяют контра-вариантный по индексу is, , и ковариантный по индексу js, , ранги тензора соответственно.
Слайд 1537. Упражнения
Записать тензорное произведение тензоров в прямой форме
Предложить способ прямого
(не индексного) обозначения свертки тензоров в произведении
Привести примеры тензоров,
имеющих различные контравариантный и ковариантный ранги.
Слайд 1547. Симметризация и альтернирование
Симметризацией тензора
по индексам i1,…,ip называется операция,
ставящая в соответствие исходному тензору тензор
Соответственно, альтернированием называется операция следующего вида
где (i1,…,ip) – перестановка индексов i1,…,ip, t = 0, если перестановка четная, и t = 1,если перестановка нечетная
Слайд 1557. Упражнения
Записать общее определение операций симметрирования и альтернирования в прямой
форме
Выписать в явном виде симметричную (антисимметричную) часть тензора третьей валентности
через симметричные и/или антисимметричные части этого же тензора
а)по первой паре индексов,
б) по последней паре индексов,
в) по первому и третьему индексам
Указание: индексы, не участвующие в операции, выделяются вертикальными черточками:
Слайд 1567. Симметричные тензоры
Тензор
называется симметричным по индексам i1,…,ip, если перестановка любой
пары индексов из данной совокупности не меняет значение тензора.
Задача. Доказать, что тензор симметричен по индексам i1,…,ip тогда и только тогда, когда он совпадает со своей симметричной частью по этой совокупности индексов:
Слайд 1578. Антисимметричные тензоры
Тензор
называется антисимметричным (кососимметричным) по индексам j1,…,jq, если перестановка
любой пары индексов из данной совокупности меняет знак тензора.
Задача. Доказать, что если тензор антисимметричен по индексам j1,…,jq, то он совпадает со своей антисимметричной частью по этой совокупности индексов:
Слайд 1588. Число линейно независимых координат антисимметричного тензора валентности p
Число линейно
независимых координат анти-симметричного тензора валентности p в n–мерном пространстве равно
числу сочетаний из n элементов по p:
Выделенные тем или иным способом независимые координаты называются главными координатами тензора
Слайд 1598. Примеры
1. Тензор валентности 2 в n–мерном пространстве имеет
n(n – 1)/2 линейно независимых координат
2.Тензор валентности n –
1 в n–мерном пространстве характеризуется совокупностью n независимых координат
3. Антисимметричные тензоры валентности n + 1 и выше в n–мерном пространстве тождественно равны нулю
Слайд 1608. Внешние формы произвольной степени p
Ковариантные антисимметричные тензоры в прямой
записи
где
При этом
Слайд 1618. Поливекторы и их делители
Поливекторы определяются как простые антисимметричные тензоры,
т.е. антисимметричные тензоры вида
где
– некоторые векторы изV n.
Векторы называются делителями поливектора (p-вектора).
Слайд 1628. Разложение поливектора в базисе
В некотором базисе координаты поливектора могут
быть записаны следующим образом
Слайд 1638. Листы антисимметричного тензора
Любой антисимметричный тензор может быть представлен в
виде разложения по поливекторам, которые в этом случае называются его
листами.
Наименьшее число листов, на которые разлагается антисимметричный тензор, является инвариантной характеристикой антисимметричного тензора.
Слайд 1648. Критерии простоты (однолистности)
Антисимметричный тензор
будет простым тогда и только тогда, когда выполняется условие
(J.A.Schouten)
либо условие (R.Weitzenbök)
либо условие (R.Weitzenbök, J.W.Givens)
выполняется при любом нечетном 1< s < p, если выполняется условие
Слайд 1658. Некоторые задачи
Покажите, что любой антисимметричный тензор валентности p и
ранга p является p-вектором.
Покажите, что антисимметричный тензор валентности n в
n–мерном пространстве определяется единственным числом. Докажите, что этот тензор является простым, или однолистным, и поэтому может быть назван n-вектором.
Слайд 1668. Некоторые задачи
Используя критерии простоты поливектора, покажите, что любой антисимметричный
тензор валентности n – 1 в n-мерном пространстве является простым
антисимметричным тензором, или (n – 1)-вектором. Т.е. существует n – 1 линейно независимых векторов , с помощью которых любой антисимметричный тензор валентности n – 1 может быть записан в виде
Слайд 1679. Контравариантные антисимметричные тензоры валентности n надV n
Антисимметричные тензоры
валентно-сти n в n-мерном пространстве определяются одним числом и являются n-векторами.
В качестве такого числа в любом наперед заданном базисе можно выбрать координату
При переходе к любому другому базису координаты n-вектора определяются значением и коэффициентами :
Слайд 1689. Контравариантные антисимметричные тензоры валентности n надV n
Из всех
ненулевых координат главной может быть
взята лишь одна. Ее значение обозначим как
где
Слайд 1699. Ковариантные антисимметричные тензоры валентности n надV n
Аналогично для
ковариантного антисимметричного тензора валентности n
Поэтому главная координата антисимметричного тензора валентности
n в новом базисе будет связана с единственной независимой координатой антисим-метричного тензора в старом базисе соотношением
Слайд 1709. Фундаментальные n-векторы
Можно построить все возможные n-векторы над пространст-вомV
n, путем умножения на любые числа из K некоторого n-вектора
, имеющего в некотором наперед заданном базисе и главную координату
Соответственно из всех ковариантных n-векторов (n-ковекторов) можно выбрать такой, что в сопряженном базисе и его главной координатой будет
Тогда все остальные n-ковекторы могут быть получены умноже-нием на любые числа из K.
Введенные таким образом n-векторы называются фундамен-тальными n-векторами относительно выделенного базиса.
Слайд 1719. Основное свойство фундаментальных n-векторов
Можно проверить непосредственно, что
независимо от
выбора базиса, относительно которого определены фундаментальные n-векторы
Величина
называется альтернатором. При n = 1он совпадает с символом Кронекера.
Слайд 1729. Важное следствие
В частности,
Задание.
Проверить данные соотношения для n =
3;4 и всех p n.
Слайд 1739. Антисимметричные тензоры, дуальные друг к другу относительно выделенного базиса
Каждому
контравариантному антисимметричному тензору ва-лентности n – p с помощью фундаментального
n-вектора поставить в соответствие некоторый антисимметричный тензор валентности p по правилу
($)
а каждому ковариантному тензору валентности p – некоторый антисимметричный тензор валентности n – p с помощью фунда-ментального n-вектора
(€)
Тензоры, связанные друг с другом соотношениями ($) и (€), называются дуальными друг к другу относительно выделенного базиса
Слайд 1749. Дуальные друг к другу антисимметричные векторы и (n –
1)-векторы
При p = 1, n – 1 из формул
($) и (€) можно получить связь между (n – 1)-(ко)вектором и (ко)вектором относительно выделенного базиса:
Одно неудобно: привязка к конкретному базису в определении и , и, соответственно в определении дуальных величин.
Слайд 17510. -плотности
Контравариантный и ковариантный n-векторы, опре-деляются одним числом, но они
не изоморфны каким-то скалярам, поскольку это число зависит от выбора
базиса.
Скалярной -плотностью веса t называется величина м , отмечаемая индексом в снизу слева от коренной буквы, указывающим на базис, в котором первона-чально задается ее значение, и индексом сверху слева, обозначающим вес величины, такая, что при преобра-зовании базиса она преобразуется по закону
Слайд 17610. -плотности и n-векторы
С точки зрения закона преобразования скаляр-ных
- плотностей
законы преобразования контравариантного
и
и ковариантного n-векторов показывают, что контравариантный n-вектор эквивалентен некоторой скалярной -плотности веса –1, а ковариантный n-вектор – скалярной -плотности веса +1.
Слайд 17710. Примеры -плотностей веса 2
Рассмотрим определители матриц, представляющих тензоры второй
валентности, контравариантный, Bij, и ковариантный Dij в некотором базисе
:
В новом базисе
Вычисляя определители тех же тензоров в новом базисе
Найдем:
т.е. определитель контравариантного тензора валентности 2 является скалярной -плотностью веса –2, , а определитель ковариант-ного тензора валентности 2 – скалярной -плотностью веса +2, .
Слайд 17810. Тензорные -плотности
Тензорной -плотностью веса t называется величина, коорди-наты которой
преобразуются закону
Все тензорные плотности можно построить путем умножения тензоров
на скалярные -плотности соответствующего веса.
Тензорные -плотности нечетного веса могут быть получены путем умножения всех возможных тензоров на -плотности веса 1 в соответствующей степени, а тензорные плотности нечетного веса – путем умножения всех возможных тензоров на определитель какого-то из тензоров второй валентности в соответствующей степени.
Сами тензоры можно рассматривать как тензорные -плотно-сти веса 0.
Слайд 17910. В частности:
Контравариантный антисимметричный тензор валентности p имеет такой же
закон преобразования при переходе от одного базиса к другому, как
и некоторая ковариантная антисимметричная -плотность валентности n – p и веса –1, а
ковариантный антисимметричный тензор валентности p при переходе от одного базиса к другому имеет такой же закон преобразования, как и некоторая контравариантная антисимметричная -плотность валентности n – p и веса +1
Слайд 18010. Скалярные плотности
Рассмотрим определители
мат-риц, представляющих контравариантный, Bij, и ковариант-ный, Dij, тензоры в некотором базисе .
Выражения
представляют собой величины, которые при преобразова-нии базиса преобразуются по закону
Величины такого рода называются обычными скалярными плотностями, или просто скалярными плотностями.
Слайд 18110. Тензорные плотности
Определение тензорной плотности веса t получается пу-тем замены
в определении тензорной -плотности оп-ределителя на его модуль :
Чтобы
отличать обозначения тензорных плотностей от тензорных -плотностей, левый нижний индекс у ко-ренной буквы, обозначающий фиксацию значений ко-ординат данной величины относительно определенного базиса или типа базисов, будем заключать под знак мо-дуля.
Тензорные плотности четного веса не отличаются от тен-зорных -плотностей.
Слайд 18210. Псевдотензоры
Произведение обычной скалярной плотности веса – 1 на скалярную
-плотность веса +1, отнесенных к одному и тому же базису
, дает величину, преобразующуюся по закону
Величина с таким законом преобразования называется W-скаляром, или псевдоскаляром.
Произведение тензора на псевдоскаляр дает псевдотензор.
Слайд 18310. Ориентация базиса
Говорят, что базисы
и
имеют разную ориентацию, если
Базисы называются со-риентированными, если > 0.
Отношение со-ориентированности разбивает все множество базисов на классы эквивалентности, которые называют базисами, имеющими правую и левую ориентации соответственно.
Определение ориентации как правой или левой зависит от договоренности (см. ниже).
Псевдотензоры и тензорные -плотности нечетного веса в отличие от тензоров и тензорных плотностей меняют знак при переходе между базисами, имеющими разную ориентацию.
Слайд 18410. Антисимметричные контравариантные плотности валентности n и веса +1 над
V n
Произведение произвольного контравариантного n-вектора и
, изоморфного скалярной -плотности веса –1, на скалярную плотность веса +1, где и – определитель некоторого ковариантного тензора валент-ности 2 в базисе и , дает контравариантную антисимметричную плотность веса +1 валентности n, имею-щую в базисе и единственную независи-мую координату
Следовательно, произвольная антисимметричная контравариантная плотность веса +1 валентности n изоморфна некоторому псевдоскаляру.
Слайд 18510. Антисимметричные ковариантные плотности валентности n и веса –1 над
V n
Произведение произвольного ковариантного n-вектора
и , изоморфного скалярной -плотности веса +1, на скалярную плотность веса –1, где – определитель некоторого контравариантного тензора ва-лентности 2 в базисе и , дает антисиммет-ричную ковариантную плотность веса –1 валентности n, имеющую в любом другом базисе и единственную независимую координату
Следовательно, произвольная антисимметричная ковариантная плотность веса –1 валентности n изоморфна некоторому псевдоскаляру.
Слайд 18610. Индифферентность антисимметричных плотностей валентности n и веса 1 надV
n иV n
В базисах одинаковой ориентации контравариантная антисимметричная
тензорная плотность валентности n веса +1, так же, как и ковариантная тензорная плотность валентности n веса –1 определяются единственной координатой, значение которой не меняется при преобразовании базиса.
Такие величины называются индифферентными относительно подгруппы преобразований базиса, не меняющих ориентацию.
При переходе к базису другой ориентации знак координаты тензора меняется. Такие величины будем называть псевдоиндифферентными.
Слайд 18710. Претендент на критерий ориентации
Среди всех возможных контравариантных антисимметрич-ных тензорных
плотностей валентности n веса +1 существует такая, значение главной координаты
которой во всех правых базисах равно +1, а во всех левых базисах – 1. Обозначим эту величину символом .
Тогда все остальные контравариантные антисимметричные тензорные плотности валентности n веса +1 могут быть по-лучены путем умножения величины на любые числа из K.
Можно ли считать знак координаты такой фундамен-тальной псевдоиндифферентной величины критери-ем, по которому определяется ориентация базиса?
Слайд 18810. Что правое, а что – левое?
Нет!
Левые базисы могут быть
определены точно так же, так как среди всех возможных контравариантных
антисимметричных тензорных плотностей валентно-сти n существует такая, единственная независимая координата которой равна +1 в левом базисе.
Различие между правым и левым точно такое же, как и различие между положительным и отрицательным электрическими зарядами: оно относительное, но не абсолютное.
Слайд 18910. И все же фундаментальнее!
Тем
не менее, вместо истинного фундаментального n-вектора
, определение которого привязано к некоторому базису , удобнее рассматривать фундаментальную антисимметричную тензорную плотность валентности n и веса +1.
Эта величина не привязана к конкретному значению в некотором наперед заданном базисе, а имеет одина-ковые значения во всех базисах одинаковой ориента-ции, по модулю равные 1.
Слайд 19010. Фундаментальная ковариантная антисимметричная тензорная плотность
Аналогичные рассуждения позволяют ввести вместо
фундаментального ковариантного n-вектора понятие ковариантной антисимметричной тензорной плотно-сти
валентности n и веса –1, главная координата которой, , имеет значение 1 в зависимости от выбора ориентации.
По сравнению с фундаментальным n-вектором преимущество выбора такой величины в качестве фундаментальной позволяет не связывать ее значе-ния с конкретным базисом , а связывать лишь знак координаты с ориентацией.
Слайд 19110. Выбор знака у E1…n и e1…n
Для тензоров над линейными
пространствами не существует связи между значениями главных координат E1…n и
e1…n.
Поэтому всегда можно положить, что в правом базисе
E1…n = 1, e1…n = 1
Тогда на эти величины распространяются те же самые выводы, что были ранее сделаны для фундаменталь-ных n-векторов
Слайд 19210. Дуальные антисимметричные величины
С помощью фундаментальных антисимметричных тензорных плотностей можно
установить соответствие (отождествление) антисимметричных тензоров валентности p и соответствующих плотностей
валентности n – p без отнесения к конкретному базису:
Обращение этих соотношений зависит от выбора знаков у и .
Слайд 19311. Действие линейных автоморфизмов на произвольные тензоры
Представим действие на произвольный
тензор
левого автоморфизма
по следующему правилу
Тогда из записи разложений
следует, что
Слайд 19411. Действие линейных автоморфизмов на произвольные тензоры
Теперь рассмотрим действие на
произвольный тензор
правого автоморфизма
по правилу
Тогда, основываясь на записи разложений
можно получить следующий закон преобразования:
Слайд 19511. Действие линейных автоморфизмов на n-векторы слева
В частности, левый автоморфизм
контравариантного n-вектора
дает n-вектор
Единственная независимая координата этого тензора
Аналогично для ковариантного n-вектора
с единственной независимой координатой
Слайд 19611. Действие линейных автоморфизмов на n-векторы справа
Для действия правых автоморфизмов
на n-векторы имеем:
Откуда для единственных независимых координат получаем правила
преобразования
Как будем определять поведение скалярных -плот-ностей под действием автоморфизмов?
Слайд 19711. Скалярные -плотности относительно автоморфизмов
Сначала надо договориться, что будем рассматривать
лишь автоморфизмы, которые сохраняют неизменной (инвариантной) свертку:
Тогда, обозначив
можно задать поведение
скалярной -плотности веса t отно-сительно левого и правого действия автоморфизма сле-дующим образом:
И нет необходимости привязываться к конкретному базису!
Слайд 19811. Скалярные плотности и псевдоскаляры относительно автоморфизмов
Аналогично определяются скалярные плотности
и псевдоскаляры относительно автоморфизмов:
левого
правого
Слайд 19911. Образование тензорных плотностей и псевдотензоров
Путем простого умножения скалярных -плотностей
и просто плотностей на произвольные тензоры можно построить соответствующие типы
тензорных плотностей с учетом направления действия линейного оператора – слева или справа.
Аналогично строятся псевдотензорные величины.
Определение таким образом -плотностей, просто плотностей и псевдотензоров не зависит от выбора базиса.
Поэтому следует определение соответствующих величин относительно преобразования базисов и относительно автоморфизмов пространства.
Слайд 20011. Другие возможности задания действия линейных автоморфизмов на величины
Если опираться
только на индексную форму записи, то можно придумать и другие
формы действия автомор-физмов – частичные: по одним индексам они левые, а по другим – правые.
Такое определение действия линейных автоморфизмов на тензоры сложно реализовать в безындексной форме записи, так как надо указать, на какой именно базисный вектор оператор действует слева, а на какой справа, а на какой вообще не действует. А это требует введения соответствующих индексов
Важно понять: в каких случаях могут возникать такого рода задачи?
Слайд 20112. Действие операторов
и
на тензоры
Линейные операторы и отображают векторы в ковекторы и наоборот.
В зависимости от направления действия (справа или слева) их можно описать с помощью двухвалентных тензоров с координатами
Слайд 20212. Действие операторов
и
на тензоры
Определим действие операторов и на тензоры
справа и слева аналогично действию автоморфизмов:
для действия слева
и для действия справа
Тензоры и имеют тип (q,p), в то время как тензор T имеет тип (p,q).
Слайд 20312. Действие операторов
и
на тензоры
Учтем, что
Тогда выражения, связывающие координаты тензоров T и `T, будут иметь вид
(£)
(¥)
Слайд 20412. Действие операторов
и
на единичный тензор
В частном случае, когда тензор T является единичным, т.е. в произвольном базисе имеет координаты, равные символам Кронекера, то из (£) и (¥) вытекает, что левым и правым образами единичного тензора будут
($$)
($$)
В случае произвольных операторов величины и могут быть абсолютно любыми.
Слайд 20512. Первые фундаментальные операторы
Из всех возможных операторов и выделим
такие операторы и
и , для которых
т.е. относительно которых единичный тензор индифферентен. Тогда координаты этих операторов при действии слева и спра-ва представляются ковариантными и контравариантными тен-зорами , связанными между собой соотношениями
(€€)
Данные операторы называются левым и правым фундамен-тальными операторами, а тензоры, реализующие их в ко-нечномерных пространствах – левым и правым фундамен-тальными тензорами соответственно.
Слайд 20612. Основное свойство первых фундаментальных тензоров
С помощью фундаментальных операторов
и , по опре-делению, устанавливается левое и
правое взаимно-одно-значные соответствия контра- и ковариантных величин, которые будем называть левоэквивалентностью и правоэквивалентностью величин по тензорам g и G.
Из (£) и (¥) видно, что тензор типа (q,p) левоэквивален-тен тензору T типа (p,q) по тензорам g и G, если в любом базисе
и, соответственно, тензор типа (q,p) правоэвивалентен тензору T типа (p,q) по тензорам g и G, если в любом базисе
Слайд 20712. Лево- и правоэквивалентные преобразования
В силу (€€) лево- и правоэквивалентные
преобразования сохраняют свертку векторов:
и вообще сохраняют любую свертку
Слайд 20812. Лево- и правоэкививалентные n-векторы
Рассмотрим произвольный контравариантный n-век-тор
. Его левый образ относительно оператора имеет координаты
а правый образ – координаты
Отсюда для главных координат тензоров имеем:
где
Слайд 20912. Лево- и правоэкививалентные n-векторы
Аналогично левый образ произвольного ковариантно-го n-вектора
относительно оператора имеет координаты
а правый образ – координаты
Тогда для главных координат тензоров имеем:
где принято во внимание, что, согласно (€€)
Слайд 210Есть ли смысл вводить новые понятия плотностей и псевдовеличин?
Есть ли
смысл говорить о плотностях и псевдотензорах относительно лево- и правоэквивалентных
преобразований?
Видимо, нет, так как при этом меняется вариантность тензора: контравариантные индексы становятся ковариантными, и наоборот.
Слайд 21113. Полное отождествление ко- и контравариантных величин
Из всех возможных лево-и
правоэквивалентных преобразова-ний можно выделить такие, при которых левое и правое
дей-ствия не отличаются по конечному результату:
В этом случае не имеет смысла различать коренные буквы у операторов и , рассматривая их как один и тот же оператор, действующий слева и справа ТАКИМ ОБРАЗОМ, что:
При этом условия вытекают друг из друга.
Оператор и реализующий его тензор называются первым фундаментальным оператором и первым фундаменталь-ным тензором соответственно.
Слайд 212Особенности и новые возможности
Комплексные линейные пространства
Слайд 213Комплексно сопряженные векторы
Если линейное пространствоV n определено над полем
комплексных чисел , то любой вектор в этом
пространстве может быть представлен в виде
где и – вещественные векторы, составляющие действительную и мнимую части вектора .
Вектор, комплексно сопряженный к ,
колинеарен вектору тогда, и только тогда, когда вещественные векторы и колинеарны: и , либо один из этих векторов – нулевой.
Слайд 214Особенности комплексных линейных пространств
Базисные векторы произвольного базиса комплексного линейного пространства
, тоже, вообще говоря, комплексны
и могут иметь в общем случае неколинеарные веществен-ную и мнимую части.
В то же время, в любом комплексном линейном простран-стве базис может быть выбран чисто вещественным.
В силу аксиомы размерности число векторов вещественного базиса должно быть равно числу векторов комплексного базиса и должно быть равно размерности пространства n.
Слайд 215Особенности комплексных линейных пространств
Отсюда вытекает, что, если вещественные векторы
и и линейно независимы, то
они представляют собой различные вещественные базисы в комплекс-ном линейном пространстве. Но тогда среди n2 векто-ров вида будет только n линейно незави-симых векторов над полем комплексных чисел.
Как их построить?
Слайд 216Особенности комплексных линейных пространств
Первый способ.
Производя разложения векторов и
по
некоторому наперед заданному вещественному базису
, найдем, что любой комплексный базис может быть представлен в виде
Слайд 217Особенности комплексных линейных пространств
По определению, можем записать
Слайд 218Особенности комплексных линейных пространств
Но
(***)
где и
– некоторые величины, подлежащие нахождению.
Из (***)
вытекает, что
Слайд 219Особенности комплексных линейных пространств
При решении каждой из систем можно воспользовать-ся
свойствами обратимости вещественных связываю-щих коэффициентов, что, например, из первой систе-мы
для и приводит к соотношениям,
из которых можно найти и в каждом конкретном случае.
Слайд 220Особенности комплексных линейных пространств – комплексно сопряженные базисы
Применение операции комплексного
сопряжения к этому базису
эквивалентно преобразованию базиса
Поэтому комплексно сопряженные базисные векторы
образуют, вообще говоря, новый базис в комплексном линейном пространстве.
Слайд 221Особенности комплексных линейных пространств – второй способ задания базиса
Второй способ.
Рассмотрим некоторый вещественный базис
Составим из его векторов всевозможные комплекс-ные линейные комбинации вида
Всего можно построить n(n – 1)/2 таких линейных ком-бинаций. Из них достаточно выделить только n/2 линейно независимых.
Соответствующие Комплексно сопряженные линейные комбинации дадут еще n/2 векторов до полного базиса.
Слайд 222Особенности комплексных линейных пространств – второй способ задания базиса
Чтобы последовательно
нумеровать координаты в этом базисе индексы, относящиеся к комплексно сопряженной
части базиса обозначаются точной сверху:
Разложение вектора в таком базисе можно пред-ставить в виде
Если вектор веществен, то в таком комплексном базисе
Слайд 223Две возможности построения сопряженного пространства над полем комплексных чисел
Первая возможность
–V n: множество линейных функционалов наV n –
реализована выше.
Вторая возможность: рассмотреть множество всех антилинейных функционалов, т.е. функционалов , обладающих следующими свойствами:
1
2
Обозначим такое линейное пространствоV *n. Базис b , взаимный к , в нем можно реализовать, опре-делив свертку, как антилинейный функционал
Слайд 224Две возможности построения сопряженного пространства над полем комплексных чисел
Чем будет
отличаться пространствоV *n от простран-стваV n?
Ничем!
В том смысле,
что они изоморфны.
Просто базисы вV *n другим способом, нежели вV n сопряжены с соответствующими базисами вV n.
Слайд 225Две возможности построения сопряженного пространства над полем комплексных чисел
Аналогично, любому
базису вV n можно поста-вить во взаимно-однозначное
соответствие его анти-линейный образ вV n:
Если , то
Пусть базис сопряжен к базису в смысле первого определения: . Тогда при условии
Слайд 226Две возможности определения
Скалярное произведение векторов
Слайд 227Скалярное произведение векторов
Скалярным произведением векторов
называется функционал, обладающий следующими свойствами:
а также удовлетворяющий одной из следующих
групп свойств:
Билинейная форма Антибилинейная форма
Слайд 228Скалярное произведение векторов
Данное определение может быть реализовано с помощью любого
ковариантного тензора второй валентности следующим образом:
билинейная форма:
антибилинейная форма:
При этом тензор
Bij не обязательно симметричен!
Его координаты формально можно определить как скалярное произведение векторов базиса:
Слайд 229Скалярное произведение ковекторов
Аналогично можно определить скалярное произведение ковекторов
:
и либо
либо
Билинейная форма Антибилинейная форма
Слайд 230Скалярное произведение ковекторов
И это определение может быть реализовано с помощью
произвольного контравариантного тензора второй валентности:
билинейная форма:
антибилинейная форма:
на который также не
накладываются условия симметричности или какие-либо другие условия.
Координаты Cij можно также формально определить как скалярное произведение векторов базиса
Слайд 231Отождествление векторов вV n и V n
. Первое определение свертки
Чтобы совместить определения скалярного произве-дения векторов и
ковекторов с первым определением свертки, необходимо принять во внимание определе-ние взаимности базисов и :
Тогда из всех возможностей реализации скалярного произведения интерес представляют лишь те, которые позволяют отождествить векторы и ковекторы, т.е. при условии, что
где gij – первый фундаментальный тензор.
Слайд 232Отождествление векторов вV n и V n
. Первое определение свертки
Поэтому определение скалярного произведения век-торов и соответствующего
скалярного произведения ковекторов будет отождествлено с их сверткой тогда и только тогда, когда скалярное произведение векторов и ковекторов задано с помощью первого фундамен-тального тензора
(*:*)
При этом любому вектору ставится во взаимно од-нозначное соответствие левый ковектор с ко-ординатами , либо правый ковектор с координатами , которые при условиях (*:*) совпадают с координатами
Слайд 233Особенности в комплексных пространствах
Если сопряженные базисы вV n построены
на множест-ве антилинейных форм, то имеется дополнительная возможность построения скалярных
произведений.
Именно, если – базис вV n, антилинейно сопряжен-ный к базису вV n: , то свертка вектора и ковектора , определенная как антилинейная форма
может быть записана как скалярное произведение второго типа
Слайд 234Метрический тензор в комплексных пространствах
где вместо (*:*) имеем:
Если на скалярное
произведение векторов в комплексном пространстве наложить условие эрмитовости
то на метрический
тензор необходимо наложить условия
В случае вещественных пространств они переходят в условия симметричности и, соответственно, отождествления правого и левого действия первого фундаментального оператора :
Слайд 235Вторая фундаментальная величина
Фундаментальная антисимметричная тензорная плотность веса + 1 и
валентности n, , и фундаментальная антисимметричная
тензорная плотность веса – 1 и валентности n, , при опускании (подъеме) индексов переходят в свои ковариантный и контравариантный аналоги соответственно:
Слайд 236Псевдотензор Леви-Чивитта
Поэтому можно ввести единый для всех случаев псевдотензор
где при
условии, что в правых базисах E1…n = 1, e1…n =
= 1, одинаковый знак «+» в обеих формулах выбирает-ся в случае, когда сигнатура первого фундаментально-го тензора содержит четное число знаков «–», а в случае нечетного числа знаков «–» в его сигнатуре – выбираются разные знаки