Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Введение в физику. 1 курс, 1 семестр Лекция 1. Основы
Содержание
- 1. Введение в физику. 1 курс, 1 семестр Лекция 1. Основы
- 2. Мои поздравления Вам, студентам, только что ступившим
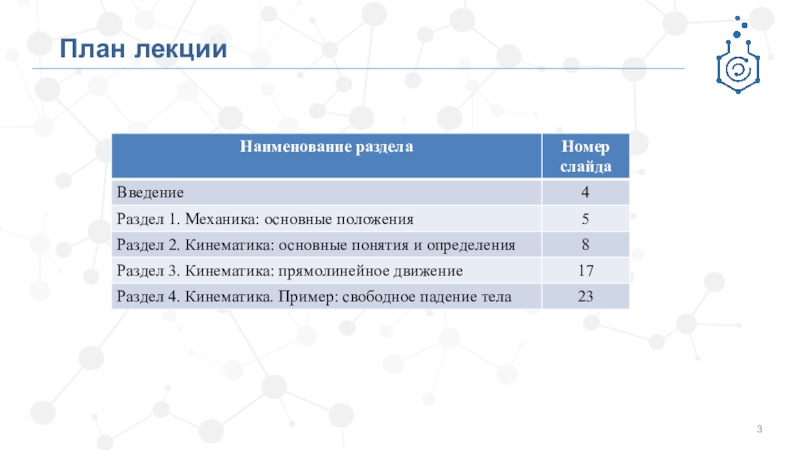
- 3. План лекции
- 4. Общие замечанияВведение Курс «Введение в физику» и
- 5. Раздел 1. Механика: основные положения
- 6. 1. Основы механики В любой стране, в любом
- 7. 1. Основы механики (продолжение) В механике используют идеализированные
- 8. Раздел 2. Кинематика: основные понятия и определения
- 9. 2. Кинематика: основные положения и определения Система отсчёта:
- 10. 2. Кинематика: основные положения и определения Единичный вектор:
- 11. 2. Кинематика: основные положения и определения Координаты точки
- 12. 2. Кинематика: характеристики движения телаТраектория: это линия,
- 13. 2. Кинематика: характеристики движения телаВекторное описание перемещения:
- 14. 2. Кинематика: скорость движения телаСкорость: это характеристика
- 15. 2. Кинематика: скорость движения телаВектор скорости v
- 16. 2. Кинематика: ускорение движущегося телаУскорение : это
- 17. Раздел 3. Кинематика: прямолинейное движение
- 18. 3. Кинематика: прямолинейное движение Прямолинейное движение : это
- 19. 3. Кинематика: виды прямолинейного движенияДвижение с постоянным ускорением (положительным, п.3.1, или отрицательным, п.4.1) называется равнопеременным.
- 20. 3. Кинематика: графики прямолинейного движенияРавномерное движение, dv/dt
- 21. 3. Кинематика: графики прямолинейного движенияГрафики равнопеременного движение
- 22. 3. Кинематика: относительность движения, сложение скоростей Движение и
- 23. Раздел 4. Кинематика. Пример: свободное падение тела.
- 24. 4. Кинематика: Пример: свободное падение тела Свободное падение
- 25. Спасибо за внимание
- 26. Скачать презентанцию
Мои поздравления Вам, студентам, только что ступившим на путь долгого и тернистого обучения в химико-технологическом университете имени Дмитрия Ивановича Менделеева!Пусть уверенности в своих силах Вам придаёт понимание того, что этот путь
Слайды и текст этой презентации
Слайд 2Мои поздравления Вам, студентам, только что ступившим на путь долгого
и тернистого обучения в химико-технологическом университете имени Дмитрия Ивановича Менделеева!
Пусть
уверенности в своих силах Вам придаёт понимание того, что этот путь уже прошли более ста поколений студентов. Значит, пройдёте и Вы!Успехов!
Слайд 4Общие замечания
Введение
Курс «Введение в физику» и другие физические курсы,
которые Вам будут читать в дальнейшем, необходимы химикам, технологам хотя
бы затем, чтобы понимать работы великих учёных-химиков. Ибо все они были химиками в той же мере, в какой и физиками. Блестящий пример – Д.И.Менделеев!Физика изучает самые общие свойства материи, вещества, т.е. наиболее простые. Законы физики обладают универсальностью, применимостью к различным явлениям и процессам.
Химия изучает более сложные свойства вещества и закономерности, но более специфические, конкретные, обладающие меньшей универсальностью.
Физика и химия взаимно дополняют друг друга, взаимно обогащают и, безусловно, сделают Вашу учёбу яркой и интересной.
Слайд 61. Основы механики
В любой стране, в любом техническом ВУЗе изучение
физики начинается с раздела «Механика».
Механика – наука о механическом движении
и механическом взаимодействии материальных тел.Механическое движение – изменение взаимного расположения материальных тел или их составных частей с течением времени.
Классическая механика Ньютона это:
- скорости движения материальных тел (v) должны быть много меньше скорости света (c), если эти скорости близки (v ≈ c), то надо применять релятивистскую механику;
- размер материального тела должен быть много больше размера микрочастиц (атомов, молекул), в противном случае надо применять квантовую механику.
Три основных раздела классической механики:
1. Статика – изучает условия равновесия материальных тел, т.е. без их движения;
2. Кинематика – изучает виды механического движения, но без действия сил;
3. Динамика – изучает силы и результат их действия.
Слайд 71. Основы механики (продолжение)
В механике используют идеализированные понятия.
Материальная точка –
тело, форма и размер которого несущественны для данной задачи.
Например,
в задаче о движении грузовика из точки А в точку В форма и размер грузовика не имеют значения. Грузовик можно
рассматривать как материальную точку.
Важное замечание: любое протяжённое тело можно рассматривать
как систему материальных точек, если это упрощает решение задачи.
Абсолютно твёрдое тело – пространственно протяжённое тело, деформацией которого в данной задаче можно пренебречь. Например, биллиардный шар.
Абсолютно упругое тело – тело с обратимыми деформациями или: форма такого тела после его деформации восстанавливается. Например, мяч для игры в футбол, теннис и т.п.
Абсолютно неупругое тело – тело, которое после прекращения внешнего силового воздействия сохраняет полностью деформированное состояние. Например, шар из пластилина.
Слайд 92. Кинематика: основные положения и определения
Система отсчёта: это совокупность выбранной
материальной точки (абсолютного твёрдого тела), являющейся точкой отсчёта (точка О),
и часов как средства измерения времени.Система координат: это совокупность осей координат (одна, две или три оси) и точки начала координат (точки отсчёта О), в которой все оси пересекаются. На каждой оси должно быть выбрано положительное направление, указанное стрелками.
Чаще всего используется прямоугольная (декартовая) система координат, когда оси координат взаимно перпендикулярны.
Традиционные обозначения осей: {OX}, {OY}, {OZ}.
Слайд 102. Кинематика: основные положения и определения
Единичный вектор: вектор длиной 1,
направлен вдоль оси координат, выходит из точки начала отсчёта О.
Единичный вектор i – направлен вдоль оси {OX}, единичный вектор j – направлен вдоль оси {OY}, единичный вектор k – направлен вдоль оси {OZ}.
Допускаются оба направления осей координат.
Слайд 112. Кинематика: основные положения и определения
Координаты точки А: совокупность координат
{x, y, z} на осях
{OX}, {OY}, {OZ}, соответственно.
Точка А описывает
положение материального тела.Обозначение радиус-вектора r, соединяющего точку начала отсчёта О и точку А, записывается так:
r = x∙i+ y∙j + z∙k
Движение точки А: это изменение координат {x(t), y(t), z(t)} во времени.
Кинематическое уравнение движения точки А (или тела) в самом общем виде:
r(t) = {x(t)∙i + y(t)∙j + z(z)∙k}
Слайд 122. Кинематика: характеристики движения тела
Траектория: это линия, описываемая в пространстве
движущейся точкой (телом).
Длина пути: это сумма элементарных длин вдоль всей
траектории. Длина пути – скалярная величина, размерность – метр (м).Перемещение: это расстояние между начальной точкой 1 и её конечным положением (точка 2). Размерность – метр (м).
Более точное определение: перемещение – это расстояние между положением тела в начальный момент времени и его положением в момент времени t.
Перемещение – векторная величина, указывающая направление куда переместилось тело.
Слайд 132. Кинематика: характеристики движения тела
Векторное описание перемещения:
r1 – радиус-вектор,
соответствующий начальному положению тела (точка М1),
r2 – радиус-вектор, соответствующий положению
тела в момент времени t (точка М2),∆r - вектор перемещения, направлен от точки М1 к точке М2.
Векторное уравнение движения тела:
r2(t) = r1(t) + ∆r(t).
Векторное уравнение перемещения тела:
∆r(t) = r2(t) - r1(t)
Слайд 142. Кинематика: скорость движения тела
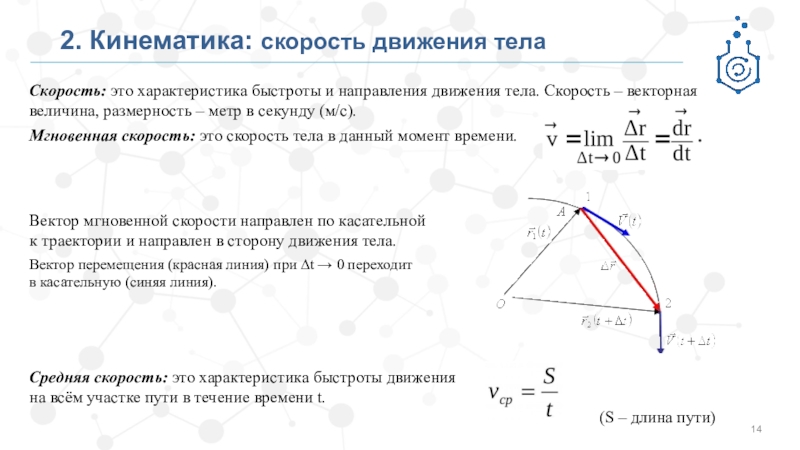
Скорость: это характеристика быстроты и направления
движения тела. Скорость – векторная величина, размерность – метр в
секунду (м/с).Мгновенная скорость: это скорость тела в данный момент времени.
Вектор мгновенной скорости направлен по касательной
к траектории и направлен в сторону движения тела.
Вектор перемещения (красная линия) при ∆t → 0 переходит
в касательную (синяя линия).
Средняя скорость: это характеристика быстроты движения
на всём участке пути в течение времени t.
(S – длина пути)
Слайд 152. Кинематика: скорость движения тела
Вектор скорости v в прямоугольной (декартовой)
системе координат записывается подобно тому, как радиус-вектор r:
v = vx∙i
+ vy∙j + vz∙k, где vx , vy , vz – проекции вектора v на оси {OX}, {OY}, {OZ}, соответственно.
Значение проекций вектора скорости рассчитываются так:
Модуль вектора скорости рассчитывается по теореме Пифагора:
Слайд 162. Кинематика: ускорение движущегося тела
Ускорение : это характеристика быстроты изменения
вектора скорости. Ускорение – векторная величина, размерность – м/с2.
Мгновенное
ускорение рассчитывается в соответствии с определением следующим образом:Вектор ускорения a есть первая производная от
вектора скорости v или вторая производная от
радиус-вектора r.
Вектор ускорения а в прямоугольной (декартовой) системе координат записывается подобно тому, как радиус-вектор r или как вектор скорости v:
а = аx∙i + аy∙j + аz∙k,
где аx , аy , аz – проекции вектора а на оси Модуль вектора ускорения
{OX}, {OY}, {OZ}, соответственно: рассчитывается также
по теореме Пифагора.
Слайд 183. Кинематика: прямолинейное движение
Прямолинейное движение : это движение, при котором
траектория тела (точки) является
прямой линией. При таком движении величины
перемещения и пути совпадают.Более строгое определение: прямолинейное движение : это движение, при котором направление вектора скорости остаётся неизменным.
Полезное замечание: В практических задачах ось системы координат, например, {OX}, выбирают так, чтобы она совпадала с направлением движения. Это существенно упрощает решение задачи.
Слайд 193. Кинематика: виды прямолинейного движения
Движение с постоянным ускорением (положительным, п.3.1,
или отрицательным, п.4.1) называется равнопеременным.
Слайд 203. Кинематика: графики прямолинейного движения
Равномерное движение, dv/dt = a =
0.
а – скорость
б – координата
в – перемещение
г – путь.
Слайд 213. Кинематика: графики прямолинейного движения
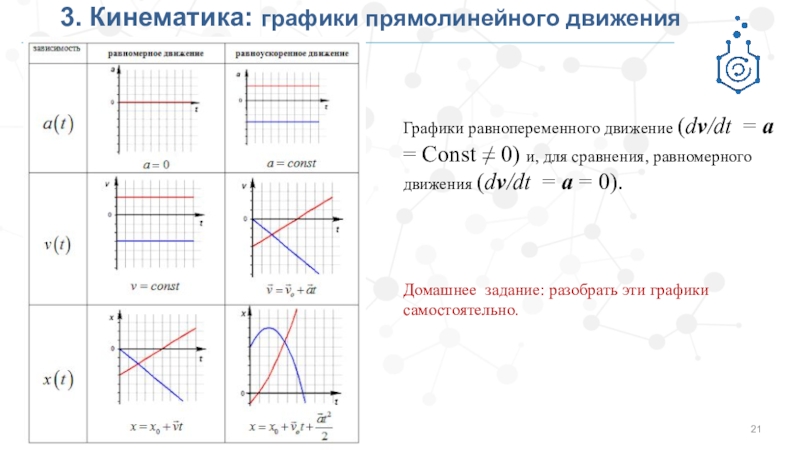
Графики равнопеременного движение (dv/dt = a
= Const ≠ 0) и, для сравнения, равномерного движения (dv/dt
= a = 0).Домашнее задание: разобрать эти графики самостоятельно.
Слайд 223. Кинематика: относительность движения,
сложение скоростей
Движение и его важнейшая характеристика
скорость зависят от выбранной системы координат (системы отсчёта).
Если тело (самолёт)
двигается со скоростью v1 в системе отсчёта К1 (точка отсчёта О1 этой системы К1 расположена на корабле), а сама эта система отсчёта, т.е. корабль, двигается со скоростью v2 в системе отсчёта К2 (точка отсчёта О2 этой системы К2 «привязана» к неподвижной суше), то скорость движения тела (самолёта) v относительно неподвижной системы отсчёта К2 (суши) равна сумме векторов: v = v1 + v2.Слайд 244. Кинематика: Пример: свободное падение тела
Свободное падение тела – это
частный случай равноускоренного движения тела под действием притяжения Земли с
начальной скоростью, равной нулю, без сопротивления воздуха (в вакууме).Экспериментально установлено, что все тела падают вблизи
поверхности Земли с одинаковым ускорением g = 9,81 м/с2.
Скорость с течением времени падения будет нарастать: v = g∙t.
Расстояние, которое пролетит тело за время t, определяется так:
h = gt2/2 или: h = v2/2g.
Домашнее задание: написать уравнения для скорости v и расстояния h
для случая, когда v0 ≠ 0. Обратить внимание на выбор точки отсчёта О.