Задачи, приводящие к теории графов. Основные понятия и определения.

Содержание

1. Задачи, приводящие к теории графов. Основные понятия и определения.
2. Историческая запискаЛеонард Эйлер (1707-1783)- швейцарец по происхождению.
3. Леонард Эйлер1707-1783
4. Задачи, приводящие к теории графовПопробуйте нарисовать закрытый
5. Задача о Кёнигсбергских мостахВпервые над задачей описанного
6. Задача о трех домах и трех колодцахВсегда
7. Слайд 7
8. Слайд 8
9. Слайд 9
10. Слайд 10
11. Слайд 11
12. Слайд 12
13. Слайд 13
14. Слайд 14
15. Слайд 15
16. Слайд 16
17. Метрические характеристики графа
18. Слайд 18
19. Слайд 19
20. Слайд 20
21. Слайд 21
22. Слайд 22
23. Слайд 23
24. Слайд 24
25. Степени вершин графа
26. Слайд 26
27. Слайд 27
28. Слайд 28
29. По степенной последовательности можно построить графы
30. Задача Существуют ли графы с данной степенной
31. Подграфы.Операции над графами
32. Слайд 32
33. 4
34. Слайд 34
35. Слайд 35
36. Слайд 36
37. Слайд 37
38. Цепи. Циклы
39. Слайд 39
40. Слайд 40
41. Слайд 41
42. Деревья
43. Граф без циклов (ациклический) называется лесом.
44. Слайд 44
45. Слайд 45
46. Слайд 46
47. Слайд 47
48. Скачать презентанцию

Историческая запискаЛеонард Эйлер (1707-1783)- швейцарец по происхождению. Приехал в Санкт-Петербург в 1727 году. Не было такой области математики XVIII века, в которой Эйлер не достиг бы заметных результатов. Например, решая головоломки

Главная
Разное
Задачи, приводящие к теории графов. Основные понятия и определения.

Слайды и текст этой презентации

Слайд 1Задачи, приводящие к теории графов. Основные понятия и определения.

Слайд 2Историческая записка
Леонард Эйлер (1707-1783)- швейцарец по происхождению. Приехал в Санкт-Петербург

в 1727 году. Не было такой области математики XVIII века,

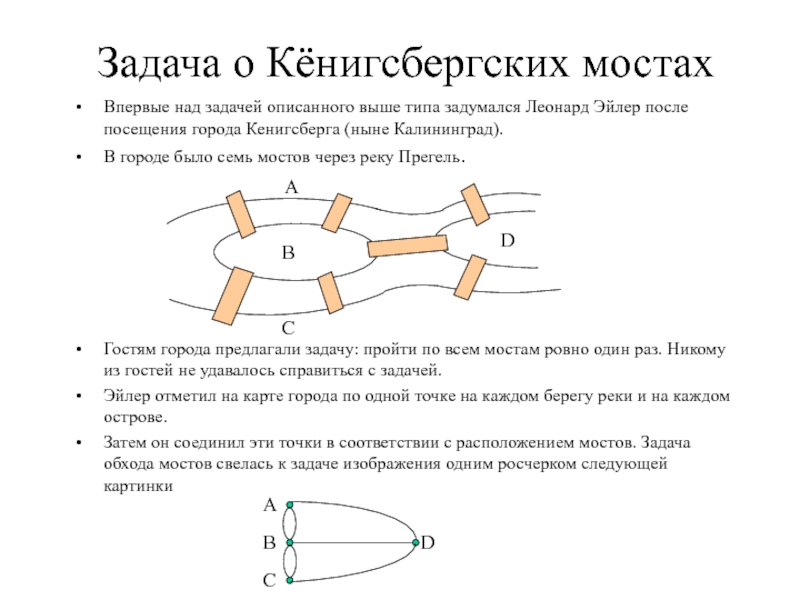
в которой Эйлер не достиг бы заметных результатов. Например, решая головоломки и развлекательные задачи, Эйлер заложил основы теории графов, ныне широко используемой во многих приложениях математики.
Напряженная работа повлияла на зрение ученого, в 1766 году он ослеп, но и после этого продолжал работу, диктуя ученикам свои статьи.
Эйлер умер в 76 лет и был похоронен на Смоленском кладбище Санкт-Петербурга. В 1957 году его прах был перенесен в Александро-Невскую лавру.

Историческая запискаЛеонард Эйлер (1707-1783)- швейцарец по происхождению. Приехал в Санкт-Петербург в 1727 году. Не было такой области

Слайд 3Леонард Эйлер
1707-1783

Слайд 4Задачи, приводящие к теории графов
Попробуйте нарисовать закрытый конверт одним росчерком,

т.е., не отрывая карандаша от бумаги и не проводя дважды

один и тот же отрезок.

А если конверт распечатать?

Задачи, приводящие к теории графовПопробуйте нарисовать закрытый конверт одним росчерком, т.е., не отрывая карандаша от бумаги и

Слайд 5Задача о Кёнигсбергских мостах
Впервые над задачей описанного выше типа задумался

Леонард Эйлер после посещения города Кенигсберга (ныне Калининград).
В городе

было семь мостов через реку Прегель.

Гостям города предлагали задачу: пройти по всем мостам ровно один раз. Никому из гостей не удавалось справиться с задачей.
Эйлер отметил на карте города по одной точке на каждом берегу реки и на каждом острове.
Затем он соединил эти точки в соответствии с расположением мостов. Задача обхода мостов свелась к задаче изображения одним росчерком следующей картинки

Задача о Кёнигсбергских мостахВпервые над задачей описанного выше типа задумался Леонард Эйлер после посещения города Кенигсберга (ныне

Слайд 6Задача о трех домах и трех колодцах
Всегда ли можно изобразить

граф на плоскости так, чтобы его ребра не пересекались? Впервые

этот вопрос возник при решении старой головоломки. Вот как ее описывает Льюис Кэрролл.
В трех домиках жили три человека, неподалеку находилось три колодца: один с водой, другой с маслом, а третий с повидлом. Однако хозяева домиков перессорились и решили провести тропинки от своих домиков к колодцам так, чтобы эти тропинки не пересекались. Первоначальный вариант по этой причине их не устраивал.

Задача о трех домах и трех колодцахВсегда ли можно изобразить граф на плоскости так, чтобы его ребра

Слайд 7

Слайд 8

Слайд 9

Слайд 10

Слайд 11

Слайд 12

Слайд 13

Слайд 14

Слайд 15

Слайд 16

Слайд 17Метрические характеристики графа

Слайд 18

Слайд 19

Слайд 20

Слайд 21

Слайд 22

Слайд 23

Слайд 24

Слайд 25Степени вершин графа

Слайд 26

Слайд 27

Слайд 28

Слайд 29По степенной последовательности можно

построить графы

Слайд 30Задача
Существуют ли графы с данной степенной последовательностью? Ответ пояснить.
1)

(1;2;3;4);
2) (13;22;3;5);
3) (0;1;2;3;42);
4) (12;23;32;4);
5) (12;32;4).
Решение.
1) Не существует, так как

все степени различные (смотри теорему 3).
2) Не существует, так как число вершин нечетной степени нечетно, а именно 5 ( смотри теорему 2).
3) Не существует(смотри задачу 1).
4) Построим граф, имеющий данную степенную последовательность

5) Не существует, так как, соединив вершину степени 4 с четырьмя из оставшихся вершин, убеждаемся, что для вершин степени 3 не достаточно смежных вершин.