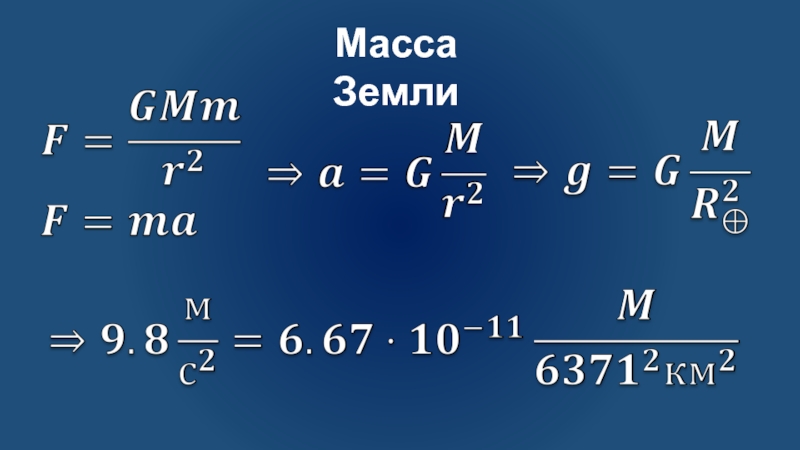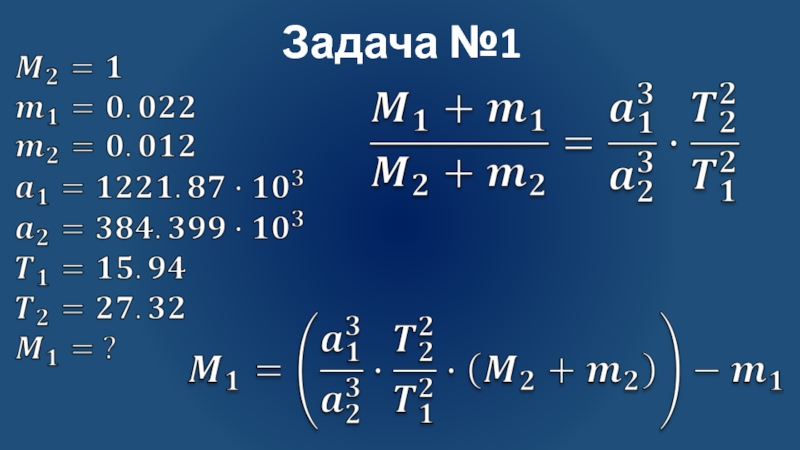Слайд 5Определение массы небесных тел на основе исследования связных систем (уточненный
III закон Кеплера)
где M1 и m1 – массы тел первой
системы;
M2 и m2 – массы тел второй системы;
a1– большая полуось тел первой системы;
a2– большая полуось тел второй системы;
T1 – период обращения тела из первой системы;
T2 – период обращения тела из второй системы.
Слайд 6Задача №1
Определите массу Сатурна (в массах Земли) путем сравнения систем
Сатурн-Титан и Земля-Луна, если известно, что спутник Сатурна Титан удален
от него на 1221.87 тыс. км. и обращается вокруг него за 15.945 земного дня.
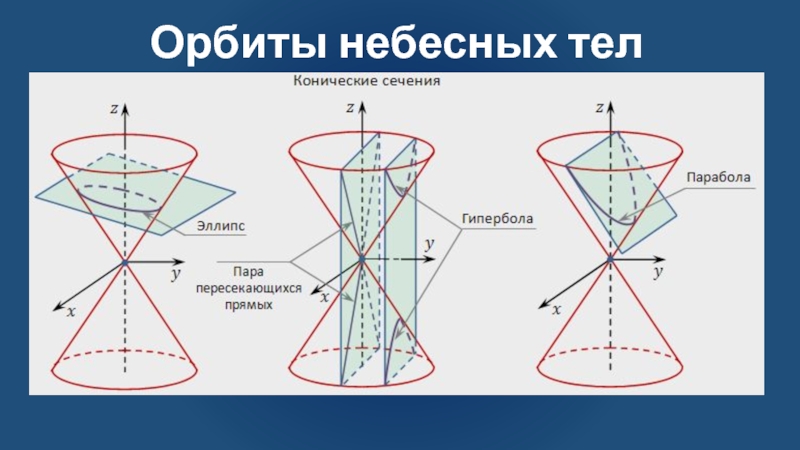
Слайд 9Орбиты небесных тел
Ньютон математически доказал, что под действием тяготения тело
m может
двигаться относительно тела М по кривым трёх типов: эллипс,
парабола
или гипербола.
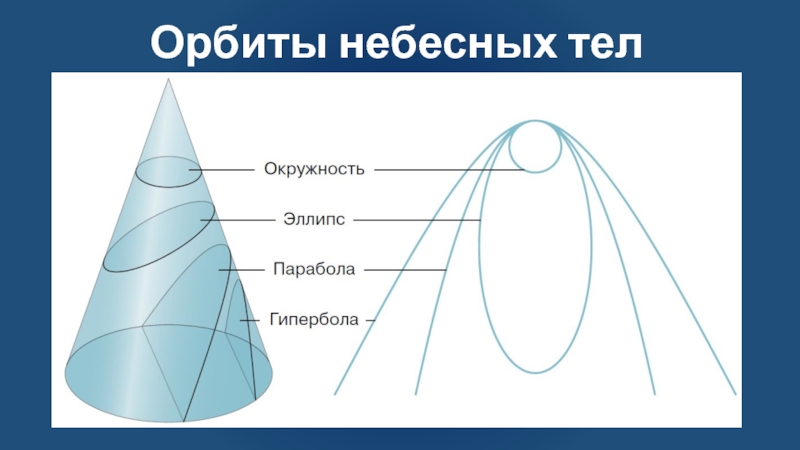
Слайд 12Орбиты небесных тел
Форма орбиты зависит от ее эксцентриситета
где b –
малая полуось; a – большая полуось.
Слайд 13Движение тела по орбите
Пусть тело массы m ≤ М движется
с линейной скоростью vк
вокруг тела М по окружности радиуса rк
Это
возможно только в том случае, если вектор скорости тела m в каждой точке орбиты перпендикулярен направлению на тело M и если движение происходит
под действием силы, создающей центростремительное ускорение.
Слайд 15Первая космическая скорость
Скорость, которую необходимо придать объекту, чтобы он смог
стать искусственным спутником и начал двигаться по круговой орбите
Слайд 16Задача №2
Определите первую космическую скорость для Земли, если ее радиус
составляет 6371 км, а масса 5.97 · 1024 кг.
Слайд 18Первая космическая скорость
Если запустить тело со скоростью, меньшей первой космической,
то оно будет двигаться по эллиптической орбите внутри круговой и
в дальнейшем упадет на массивное тело.
Если запустить с большей, то тело будет двигаться по эллиптической орбите за пределами круговой
Слайд 21Задача №3
Определите вторую космическую скорость для Земли, если ее радиус
составляет 6371 км, а масса 5.97 · 1024 кг.
Слайд 23Третья космическая скорость
Наименьшая скорость, которую надо придать объекту, для преодоления
гравитационного притяжения своей звездной системы