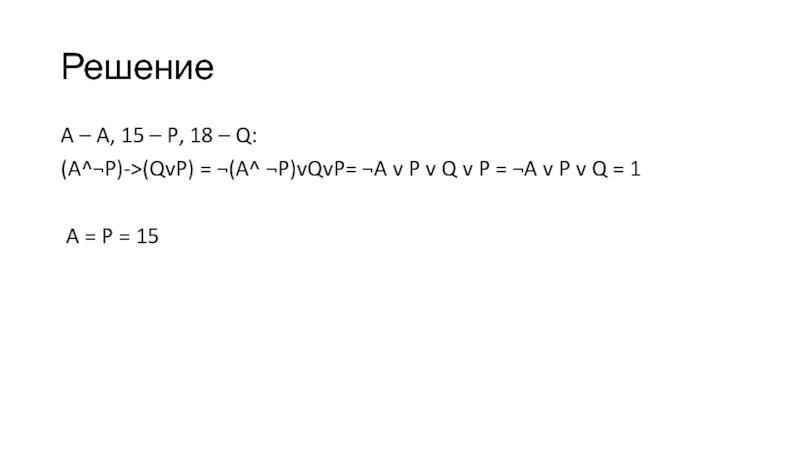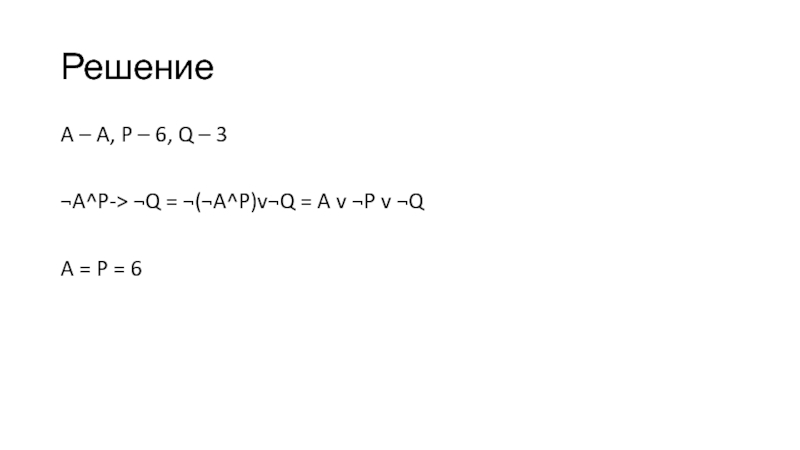Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Занятие 11
Содержание
- 1. Занятие 11
- 2. Задание B18Преобразование логических выражений
- 3. На прошлом занятии мы разобрали:Множества ((x ∈
- 4. Сегодня мы разберем¬ДЕЛ(x, А) → (ДЕЛ(x, 6)
- 5. Задание 1
- 6. РешениеA – A, 15 – P, 18
- 7. Задание 2
- 8. Решение18 – P, 21 – Q, A
- 9. Задание 3
- 10. РешениеA – A, P – 6, Q
- 11. Задание 4Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится
- 12. РешениеВведём обозначения A = ДЕЛ(x, А), P = ДЕЛ(x, 6) и Q = ДЕЛ(x, 4)Введём множества:A —
- 13. РешениеA+ ¬P+ ¬QA должно покрыть то, что
- 14. Задание 5Обозначим через m&n поразрядную конъюнкцию неотрицательных целых чисел m и n.
- 15. Решение¬Х → (Y → ¬Z) = Х
- 16. Задание 6Для какого наименьшего неотрицательного целого числа А формула x &
- 17. Решение¬Х → (Y → ¬Z) = Х
- 18. Задание 7
- 19. РешениеИмеем импликацию Z17ZA → Z28Z45 или Z(17 or А) →
- 20. Задание 8 Для какого наименьшего неотрицательного целого числа
- 21. РешениеХ + (Y → Z) = Х
- 22. Задание B10+Комбинаторика LevelUp
- 23. Размещения с повторениямиРазмещениями с повторениями называются упорядоченные
- 24. Размещения с повторениямиНа световой панели в ряд
- 25. Размещения с повторениями3^4=81
- 26. Перестановки с повторениямиПусть в исходную совокупность входит
- 27. Перестановки с повторениямиНа световом табло в один
- 28. Перестановки с повторениямиЗаметим, что все лампочки исходной
- 29. Сочетания с повторениями Сочетаниями с повторениями называются неупорядоченные
- 30. Сочетания с повторениями Для составления некоторого кода используются
- 31. Сочетания с повторениями Поскольку длина кодовых слов равна
- 32. Задание 1Вася составляет 5-буквенные слова из четырехбуквенного
- 33. РешениеВарианты размещения двух букв АОставшиеся три буквы = 3^3 = 27Всего вариантов 10*27=270
- 34. Задание 2а) Из класса, в котором учатся
- 35. Решение
- 36. Задание 3На плоскости отмечено 10 точек так,
- 37. Решение
- 38. Задание 4Рота состоит из трёх офицеров, шести
- 39. Решение
- 40. Скачать презентанцию
Задание B18Преобразование логических выражений
Слайды и текст этой презентации
Слайд 3На прошлом занятии мы разобрали:
Множества
((x ∈ P) → (x
∈ A)) ∨ (¬(x ∈ A) → ¬(x ∈ Q))
< A) → (x2 < 100)) ∧ ((y2 ≤ 64) → (y ≤ A))Слайд 6Решение
A – A, 15 – P, 18 – Q:
(A^¬P)->(QvP) =
¬(A^ ¬P)vQvP= ¬A v P v Q v P =
¬A v P v Q = 1A = P = 15
Слайд 11Задание 4
Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на
натуральное число m».
Для какого наибольшего натурального числа А формула
¬ДЕЛ(x, А) → (ДЕЛ(x, 6)
→ ¬ДЕЛ(x, 4))тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной x)?
Слайд 12Решение
Введём обозначения A = ДЕЛ(x, А), P = ДЕЛ(x, 6) и Q = ДЕЛ(x, 4)
Введём множества:
A — множество натуральных чисел,
для которых выполняется условие A
P — множество натуральных чисел, для которых выполняется
условие PQ — множество натуральных чисел, для которых выполняется условие Q
Слайд 13Решение
A+ ¬P+ ¬Q
A должно покрыть то, что не покрывает ¬P+
¬Q, то есть ¬(¬P+ ¬Q)
= P*Q
это множество всех чисел, которые
делятся одновременно на 4 и 6 (все числа, кратные 4 и 6), то есть, 12, 24, 36 и т. д. (заметим, что 12 — это наименьшее общее кратное чисел 4 и 6). Для того, чтобы перекрыть эти числа, можно выбрать в качестве A любой делитель числа 12, то есть, 1, 2, 3, 4, 6 или 12; наибольшее из этих чисел — 12.Слайд 14Задание 5
Обозначим через m&n поразрядную конъюнкцию неотрицательных целых чисел m и n. Так, например, 14&5
= 11102&01012 = 01002 = 4.
Для какого наименьшего неотрицательного целого числа А формула
x&25 ≠
0 → (x&17 = 0 → x&А ≠ 0)тождественно истинна (т.е. принимает значение 1 при любом неотрицательном целом значении переменной х)?
Слайд 15Решение
¬Х → (Y → ¬Z) = Х + (Y →
¬Z) = Х + ¬Y + ¬Z = X +
¬(YZ) = YZ → XИмеем импликацию Y17ZA → X25 или Y(17 or A) → Z25. Запишем число 25 в двоичной системе счисления: 2510 = 110012. Единичные биты, стоящие в правой части, должны являться единичными битами левой. Поскольку 1710 = 100012, двоичная запись искомого числа А должна содержать единичный бит в третьем разряде (как обычно, считая справа налево, начиная с нуля).
Тем самым, наименьшее А = 10002 = 810.
Слайд 16Задание 6
Для какого наименьшего неотрицательного целого числа А формула
x & 29 ≠ 0
→ (x & 12 = 0 → x & А ≠ 0)
тождественно истинна (то есть
принимает значение 1 при любом неотрицательном целом значении переменной х)?Слайд 17Решение
¬Х → (Y → ¬Z) = Х + (Y →
¬Z) = Х + ¬Y + ¬Z = X +
¬(YZ) = YZ → X.Имеем импликацию Z12ZA → Z29 или Z(12 or A) → Z29. Запишем число 29 в двоичной системе счисления: 2910 = 111012. Единичные биты, стоящие в правой части, должны являться единичными битами левой. Поскольку 1210 = 011002, двоичная запись искомого числа А должна содержать единичные биты в нулевом и четвертом разрядах (как обычно, считая справа налево, начиная с нуля).
Тем самым, наименьшее А = 100012 = 1710.
Слайд 19Решение
Имеем импликацию Z17ZA → Z28Z45 или Z(17 or А) → Z(28 or 45).
Поскольку 2810 = 111002, 4510 = 1011012, для побитовой дизъюнкции имеем: 28or45 = 111101. Тогда Z(17
or А) = Z61.Импликация принимает вид Z(17 or A) → Z61. Единичные биты двоичной записи числа 61, должны являться единичными битами левой части. Поэтому в побитовой дизъюнкции 17orA единицы должны стоять на нулевой, второй, третьей, четвертой и пятой позициях (как обычно, считая справа налево, начиная с нуля). Запишем числа 17, А и 61 в двоичной системе счисления, и выясним, что наименьшее число, дающее при поразрядной дизъюнкции единицы на указанных позициях:
17: 010001
A: 1?110?
61: 111101
В записи наименьшего числа, дающего при поразрядной дизъюнкции с числом 17 единицы в необходимых разрядах, на месте знаков ? должны стоять нули. Тем самым, искомым числом является А = 1011002 = 4410.
Ответ: 44.
Слайд 20Задание 8
Для какого наименьшего неотрицательного целого числа А формула
x&51 =
0 ∨ (x&41 = 0 → x&А = 0)
тождественно истинна (т. е.
принимает значение 1 при любом неотрицательном целом значении переменной x)?Слайд 21Решение
Х + (Y → Z) = Х + (¬Y +
Z) = Х + Z + ¬Y = Y →
(X + Z) = (Y → X) + (Y → Z).Заметим, что первое слагаемое логической суммы является импликацией Z41 → Z51, которая не является истинной для всех х (см. ниже). Тогда необходимо и достаточно, чтобы второе слагаемое логической суммы было тождественно истинным.
Действительно, например, для х = 2 поразрядная конъюнкция с числом 41 дает 0, а с числом 51 дает 2. Поэтому импликация (2&41) → (2&51) принимает вид 1 → 0 — ложь.
2: 000010
41: 101001
2&41: 000000, то есть 2&41 = 0. Высказывание 2&41 = 0 истинно.
2: 000010
51: 110011
2&51: 000010 = 2, то есть 2&51 = 2. Высказывание 2&51 = 0 ложно.
Итак, импликация Z41 → ZA должна быть тождественно истинной. Запишем число 41 в двоичной системе счисления: 4110 = 1010012. Единичные биты, стоящие в правой части, должны являться единичными битами левой. Поэтому в правой части единичными битами независимо друг от друга могут быть (а могут не быть) только нулевой, второй и четвертый биты (как обычно, считая справа налево, начиная с нуля). Поскольку искомое A — наименьшее неотрицательное целое число, в его записи нет единичных битов.
Тем самым, наименьшее А = 0000002 = 010.
Слайд 23Размещения с повторениями
Размещениями с повторениями называются упорядоченные выборки, содержащие k
элементов из данных n элементов, причем каждый элемент исходной совокупности
может участвовать в размещении несколько раз.Формула для расчета количества размещений с повторениями
Слайд 24Размещения с повторениями
На световой панели в ряд расположены 4 лампочки,
каждая из которых может гореть красным, жёлтым или зелёным цветом.
Сколько различных сигналов можно передать с помощью панели (все лампочки должны гореть, порядок цветов имеет значение)?Слайд 26Перестановки с повторениями
Пусть в исходную совокупность входит n1 элементов первого типа,
n2 - второго типа, …, nk – k-го типа, при этом n1 +
n2 + …+ nk = n. Всевозможные упорядоченные выборки, составленные из всех данных n элементов, называются перестановками с повторениями.Формула для расчета количества cочетаний с повторениями
Слайд 27Перестановки с повторениями
На световом табло в один ряд располагаются шесть
лампочек. Сколько различных сигналов можно получить, имея две зеленые и
четыре красные лампочки? Все лампочки должны гореть.Слайд 28Перестановки с повторениями
Заметим, что все лампочки исходной совокупности должны располагаться
на табло (4 + 2 = 6). Так как «все
лампочки должны гореть», то сигналы будут отличаться только порядком цветов. Значит, комбинаторная схема – перестановки с повторениями.Слайд 29Сочетания с повторениями
Сочетаниями с повторениями называются неупорядоченные выборки, содержащие k
элементов из данных n элементов, причем каждый элемент исходной совокупности
может участвовать в сочетании несколько раз.Формула для расчета количества сочетаний с повторениями
Слайд 30Сочетания с повторениями
Для составления некоторого кода используются цифры 1, 2,
3. Кодовые слова должны удовлетворять следующим свойствам:
1) Длина кодовых слов
равна 3;2) Кодовые слова могут содержать одинаковые цифры;
3) Кодовые слова, отличающиеся только порядком цифр, считаются одинаковыми.
Сколько вариантов кодовых слов можно составить?
Слайд 31Сочетания с повторениями
Поскольку длина кодовых слов равна 3, то выборки
из 3 по 3. Определим комбинаторную схему: из пункта 3
следует, что выборка неупорядоченная при этом «Кодовые слова могут содержать одинаковые цифры», значит, выборки – сочетания с повторениями.Действительно, таких кодовых слов ровно 10: 111 112 113 122 123 133 222 223 233 333