Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Занятие 24. (2 часа) Изгиб. Классификация видов изгиба. Построение эпюр
Содержание
- 1. Занятие 24. (2 часа) Изгиб. Классификация видов изгиба. Построение эпюр
- 2. 24.1. Основные определенияИзгибом называется такой вид нагружения,
- 3. Плоскость, в которой расположены внешние силы и
- 4. Если силовая плоскость совпадает с главной плоскостью
- 5. 24.2. Внутренние силовые факторы при изгибеРассмотрим балку,
- 6. Под действием внешней пары сил участок стремится
- 7. Продольная сила N в сечении равна нулю.
- 8. Линия пересечения нейтрального слоя с плоскостью поперечного
- 9. Рассмотрим равновесие участка бруса от свободного конца
- 10. В сечении бруса 2-2 действует поперечная сила,
- 11. ВыводыПри чистом изгибе в поперечном сечении балки
- 12. 24.3. Построение эпюр поперечных сил и изгибающих
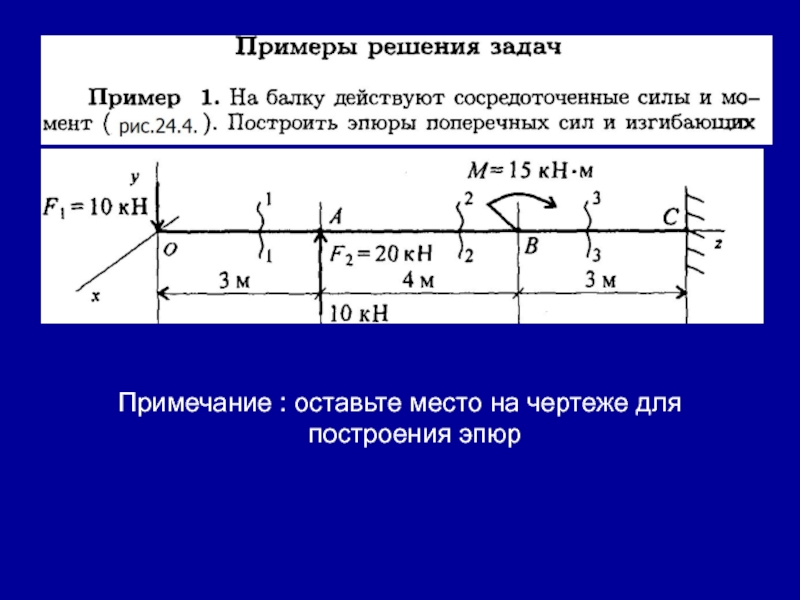
- 13. Примечание : оставьте место на чертеже для построения эпюр
- 14. РешениеПоследовательно по участкам нагружения рассматриваем внутренние силовые
- 15. Составим уравнения равновесия.1. Рассмотрим участок 1 (рис. 24.6.а).рис. 24.6.аСила Q1 — отрицательна.
- 16. Сила Q на участке 1 постоянна. Mx
- 17. 2. Рассмотрим участок 2 (рис. 24.6.б).рис. 24.6.б
- 18. Слайд 18
- 19. 3. Рассмотрим участок 3 (рис. 24.6.в).Рис. 24.6.в
- 20. Обращаем внимание, что для точки В получено
- 21. 4. Построение эпюр. Порядок построения эпюр остается
- 22. Правила построения эпюр (рис. 24.4. и рис.24.7.):
- 23. 1. Для участка, где отсутствует распределенная нагрузка,
- 24. Пример 2. На двухопорную балку действуют сосредоточенные
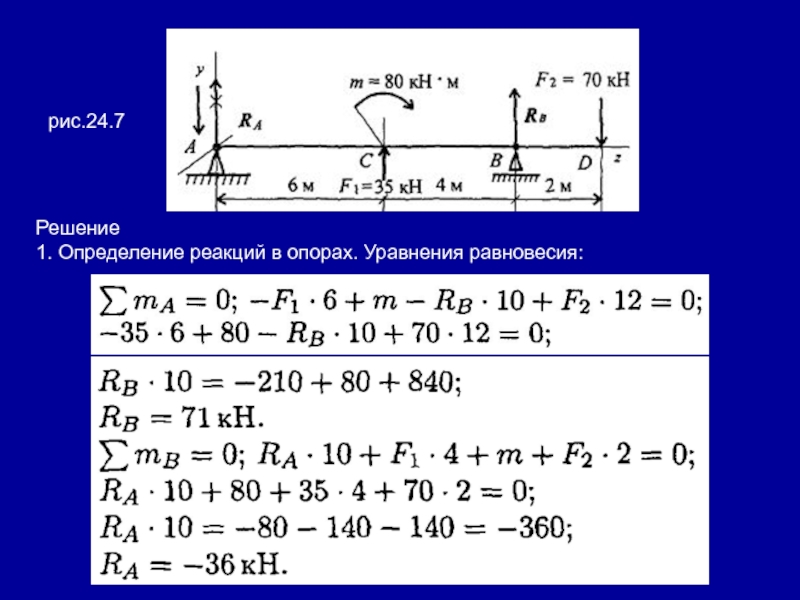
- 25. рис.24.7Решение1. Определение реакций в опорах. Уравнения равновесия:
- 26. Реакция в опоре RA направлена в обратную сторону. Проверка: Реакции определены верно.
- 27. 2. Для упрощения расчетов при построении эпюр
- 28. Участок 2 (от точки С справа до
- 29. Момент в точке B определяется по зависимости
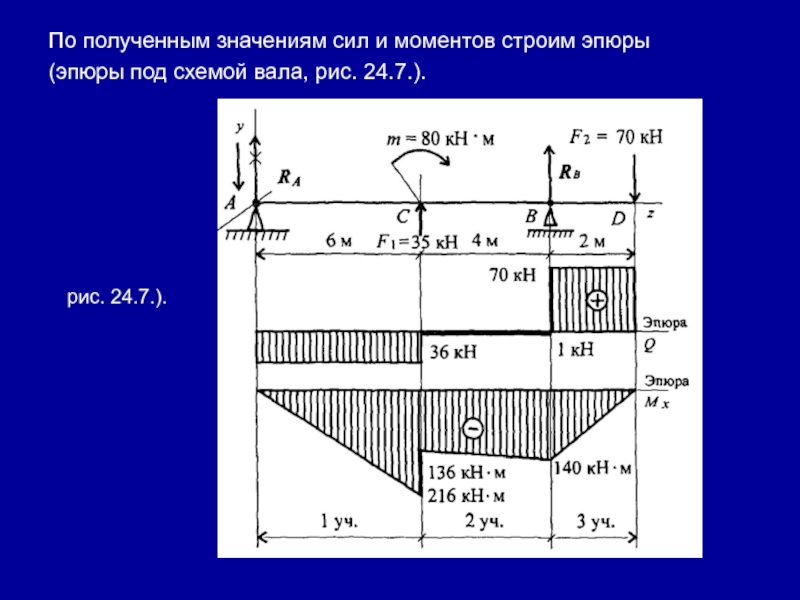
- 30. По полученным значениям сил и моментов строим эпюры (эпюры под схемой вала, рис. 24.7.).рис. 24.7.).
- 31. Занятие 25. (2 часа) Контрольная работа №3
- 32. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Занятие 24. (2 часа) Изгиб. Классификация видов изгиба. Построение эпюр поперечных
сил и изгибающих моментов
Слайд 224.1. Основные определения
Изгибом называется такой вид нагружения, при котором в
поперечном сечении бруса возникает внутренний силовой фактор — изгибающий момент.
Брус, работающий на изгиб, называют балкой.
Изображен брус, закрепленный справа (защемление), нагруженный внешними силами и моментом (рис. 24.1).
рис. 24.1
Слайд 3Плоскость, в которой расположены внешние силы и моменты, называют силовой
плоскостью.
Если все силы лежат в одной плоскости, изгиб называют плоским.
Плоскость,
проходящая через продольную ось бруса и одну из главных центральных осей его поперечного сечения, называется главной плоскостью бруса.Рис.24.2.
Слайд 4Если силовая плоскость совпадает с главной плоскостью бруса, изгиб называют
прямым (рис. 24.1).
Если силовая плоскость не проходит через главную плоскость
бруса, изгиб называют косым изгибом (рис. 24.2).рис. 24.1
рис. 24.2
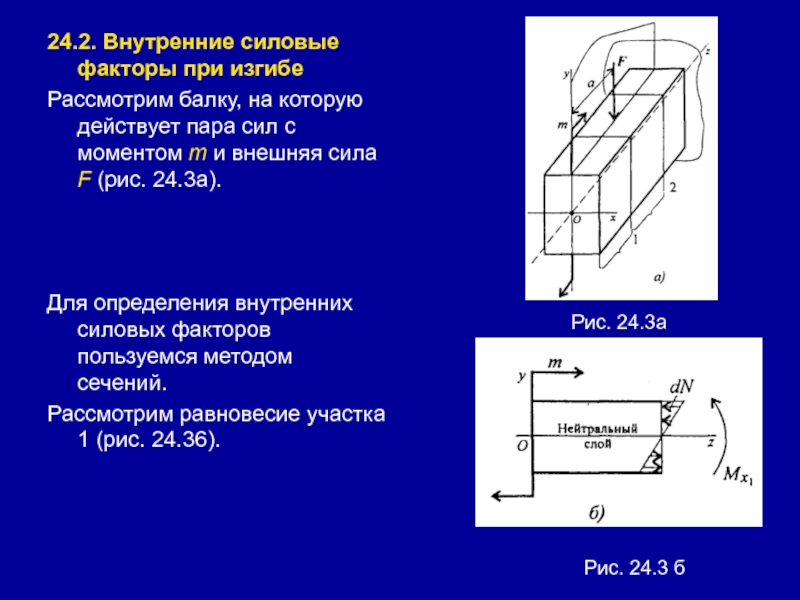
Слайд 524.2. Внутренние силовые факторы при изгибе
Рассмотрим балку, на которую действует
пара сил с моментом m и внешняя сила F (рис.
24.3а).Для определения внутренних силовых факторов пользуемся методом сечений.
Рассмотрим равновесие участка 1 (рис. 24.36).
Рис. 24.3а
Рис. 24.3 б
Слайд 6Под действием внешней пары сил участок стремится развернуться по часовой
стрелке. Силы упругости, возникающие в сечении 1, удерживают участок в
равновесии.Продольные силы упругости выше оси бруса направлены налево, а силы ниже оси направлены направо.
Таким образом, при равновесии участка 1 получим:
Слайд 7Продольная сила N в сечении равна нулю. Момент сил упругости
относительно оси Ох может быть получен, если суммировать элементарные моменты
сил упругости в сечении 1-1 относительно оси Ох:Этот момент называют изгибающим моментом Мх = Ми.
Из схемы вала на рис. 24.3.б видно, что часть волокон (выше оси) испытывают сжатие, а волокна ниже оси растянуты.
Следовательно, в сечении должен существовать слой не растянутый и не сжатый, где напряжения σ равны нулю.
Такой слой называют нейтральным слоем (НС).
Слайд 8Линия пересечения нейтрального слоя с плоскостью поперечного сечения бруса называют
нейтральной осью.
Нейтральный слой проходит через центр тяжести сечения. Здесь нейтральный
слой совпадает с осью Oх.Практически величина изгибающего момента в сечении определяется из уравнения равновесия:
Таким образом, в сечении 1-1 продольная сила равна нулю, изгибающий момент в сечении постоянен.
Изгиб, при котором в поперечном сечении бруса возникает только изгибающий момент, называется чистым изгибом.
Слайд 9Рассмотрим равновесие участка бруса от свободного конца до сечения 2
(рис. 24.3в).
Рис. 24.3 в
Запишем уравнения равновесия для участка бруса:
Слайд 10В сечении бруса 2-2 действует поперечная сила, вызывающая сдвиг.
Изгибающий момент в сечении:
Z2 — расстояние от сечения 2
до начала координат.Изгибающий момент зависит от расстояния сечения до начала координат.
Изгиб, при котором в поперечном сечении бруса возникает изгибающий момент и поперечная сила, называется поперечным изгибом.
Слайд 11Выводы
При чистом изгибе в поперечном сечении балки возникает только изгибающий
момент, постоянный по величине.
При поперечном изгибе в сечении возникает изгибающий
момент и поперечная сила.Изгибающий момент в произвольном сечении балки численно равен алгебраической сумме моментов всех внешних сил, приложенных к отсеченной части, относительно рассматриваемого сечения.
Поперечная сила в произвольном сечении балки численно равна алгебраической сумме проекций всех внешних сил, действующих на отсеченной части на соответствующую ось.
Слайд 1224.3. Построение эпюр поперечных сил и изгибающих моментов. Основные правила
построения эпюр
Эпюры поперечных сил и изгибающих моментов можно строить, предварительно
разделив балку на участки нагружения и составляя уравнения, выражающие изменения Q и Мх по участкам.Напомним, что границы участков нагружения — это сечения, в которых приложены внешние нагрузки.
Слайд 14Решение
Последовательно по участкам нагружения рассматриваем внутренние силовые факторы в сечениях.
Силовые факторы определяем из условий равновесия отсеченной части. Для каждого
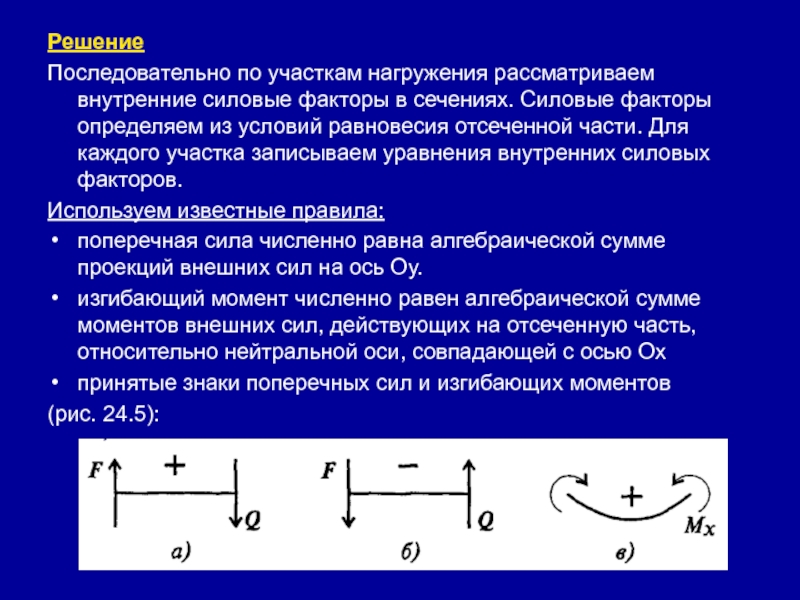
участка записываем уравнения внутренних силовых факторов.Используем известные правила:
поперечная сила численно равна алгебраической сумме проекций внешних сил на ось Оу.
изгибающий момент численно равен алгебраической сумме моментов внешних сил, действующих на отсеченную часть, относительно нейтральной оси, совпадающей с осью Ох
принятые знаки поперечных сил и изгибающих моментов
(рис. 24.5):
Слайд 15Составим уравнения равновесия.
1. Рассмотрим участок 1 (рис. 24.6.а).
рис. 24.6.а
Сила Q1
— отрицательна.
Слайд 16Сила Q на участке 1 постоянна.
Mx — отрицательный.
Изгибающий момент
меняется по линейному закону, график — прямая линия.
Слайд 20Обращаем внимание, что для точки В получено два значения изгибающих
моментов: из уравнения для участка 2 левее точки В и
из уравнения для участка 3 — правее точки В.Это объясняется тем, что именно в этой точке приложен внешний момент и поэтому внутренний момент сил упругости меняется
В точках приложения внешнего момента на эпюре моментов появится скачок, равный величине приложенного момента.
Поперечная сила в точке В для второго и третьего участков одинакова.
Следовательно, приложение внешнего момента не отражается на эпюре поперечных сил.
График поперечной силы на участке 3 — прямая линия.
График изменения изгибающих моментов на третьем участке также прямая линия.
Слайд 214. Построение эпюр.
Порядок построения эпюр остается прежним: масштабы эпюр
выбираются отдельно, исходя из значений максимальных сил и моментов.
Графики обводятся
толстой основной линией и заштриховываются поперек. На графиках указываются значения поперечных сил, изгибающих моментов и единицы измерения.Слайд 231. Для участка, где отсутствует распределенная нагрузка, поперечная сила постоянна,
а изгибающий момент меняется по линейному закону.
2. В частном случае,
когда поперечная сила на участке равна нулю, изгибающий момент постоянен (чистый изгиб), график — прямая линия, параллельная продольной оси 3. В том месте, где к балке приложена внешняя сосредоточенная сила, на эпюре Q возникает скачок на величину приложенной силы, а на эпюре моментов — излом.
4. В сечении, где к балке приложена пара сил (сосредоточенный момент), на эпюре Ми возникает скачок на величину момента этой пары. Поперечная сила при этом не изменяется.
5. В сечении на конце балки поперечная сила равна приложенной в этом сечении сосредоточенной силе или реакции в заделке.
6. На свободном конце балки или шарнирно опертом конце момент равен нулю, за исключением случаев, когда в этом сечении приложена пара сил (внешний момент).
Слайд 24Пример 2.
На двухопорную балку действуют сосредоточенные силы и моменты
(рис. 24.7.). Построить эпюры поперечных сил и изгибающих моментов.
Для двухопорной
балки построение эпюр начинают с определения опорных реакций балки. Для их определения используем систему уравнений равновесия,
составляем два уравнения моментов относительно шарнирных опор.
Затем проводим проверку правильности решения по уравнению
Слайд 272. Для упрощения расчетов при построении эпюр поперечным сил и
изгибающих моментов можно провести расчет по характерным точкам без составления
уравнений.Для этого используют известные связи между поперечной силой и изгибающим моментом и правила построения эпюр.
Участок 1 (от точки А до точки С).
В точке А приложена реакция RA, направленная вниз. Поперечная сила на участке постоянна:
Момент в точке А равен нулю.
Точка С (слева). Приложена внешняя сила F1= 35 кН, направленная вверх, — здесь возникнет скачок вверх на величину 35 кН.
Момент в точке С (слева) может быть рассчитан по известной зависимости
Слайд 28Участок 2 (от точки С справа до точки B).
Поперечная сила
в точке С (справа) равна
В точке С приложена внешняя
пара сил с моментом 80кН·м, следовательно, здесь проявляется скачок на величину приложенного момента: Поперечная сила на втором участке постоянна
Слайд 29Момент в точке B определяется по зависимости
Справа и слева
от точки в момент имеет одинаковые значения.
Участок 3 (от точки
B(справа) до точки D).В точке в приложена внешняя сила RB. Здесь появляется скачок на величину 71 кН,
Дальше по участку поперечная сила не изменяется. Момент в точке D равен нулю, т.к. здесь не приложена внешняя пара сил: MD = 0.
Рассмотрение поперечных сил и изгибающих моментов можно было провести и справа налево.