Слайд 2Запросы в поисковых системах
Задание B17
Слайд 4Задание 1
Некоторый сегмент сети Интернет состоит из 1000 сайтов. Поисковый
сервер в автоматическом режиме составил таблицу ключевых слов для сайтов
этого сегмента. Вот ее фрагмент:
Сколько сайтов будет найдено по запросу «(принтер | сканер) & монитор», если по запросу «принтер | сканер» было найдено 450 сайтов, по запросу «принтер & монитор» — 40, а по запросу «сканер & монитор» — 50.
Слайд 5Решение
Принтер | сканер = 450 следовательно пересечений нет
принтер & сканер
= 0
Принтер & монитор + сканер & монитор = 50
+ 40 = 90
Слайд 6Задание 2
В таблице приведены запросы и количество страниц, которые
нашел поисковый сервер по этим запросам в некотором сегменте Интернета:
Сколько
страниц (в тыс.) будет найдено по запросу крейсер & линкор
Слайд 7Решение
Всего страниц крейсер | линкор = 7000,
4800+4500-7000=2300
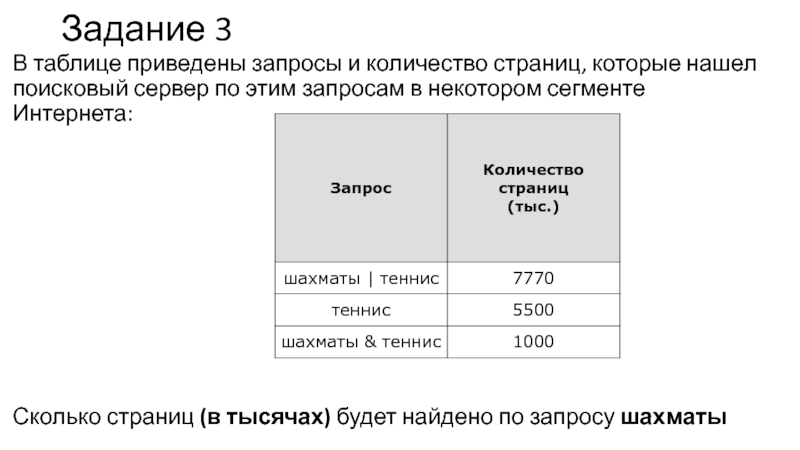
Слайд 8Задание 3
В таблице приведены запросы и количество страниц, которые
нашел поисковый сервер по этим запросам в некотором сегменте Интернета:
Сколько
страниц (в тысячах) будет найдено по запросу шахматы
Слайд 9Решение
Шахматы ИЛИ теннис = 7770
Теннис = 5500
Шахматы И теннис =
1000
Чисто шахматы = 7770-5500, но общих с теннисом еще +
1000
Итого 7770-5500+1000=3270
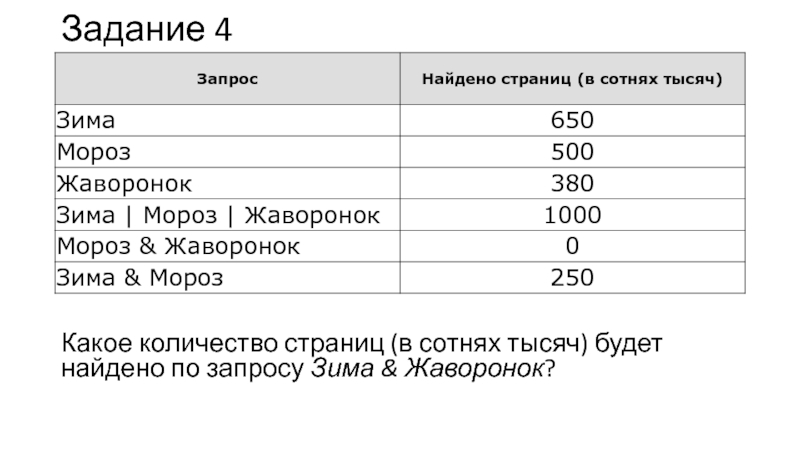
Слайд 10Задание 4
Какое количество страниц (в сотнях тысяч) будет найдено
по запросу Зима & Жаворонок?
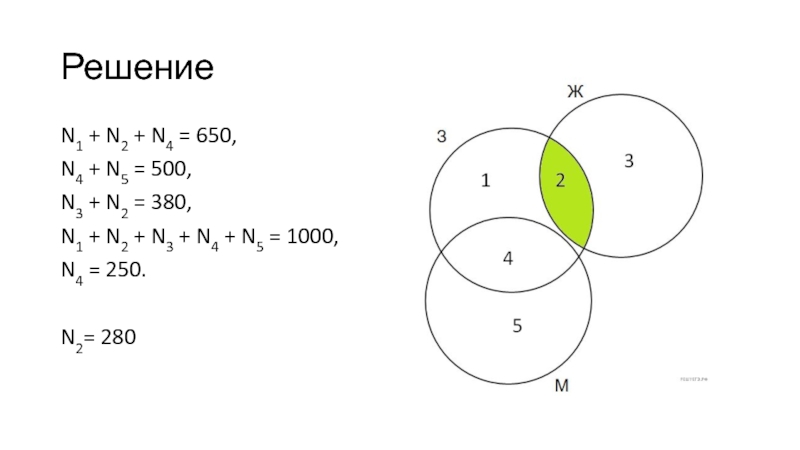
Слайд 11Решение
N1 + N2 + N4 = 650,
N4 + N5 = 500,
N3 + N2 = 380,
N1 + N2 + N3 +
N4 + N5 = 1000,
N4 = 250.
N2= 280
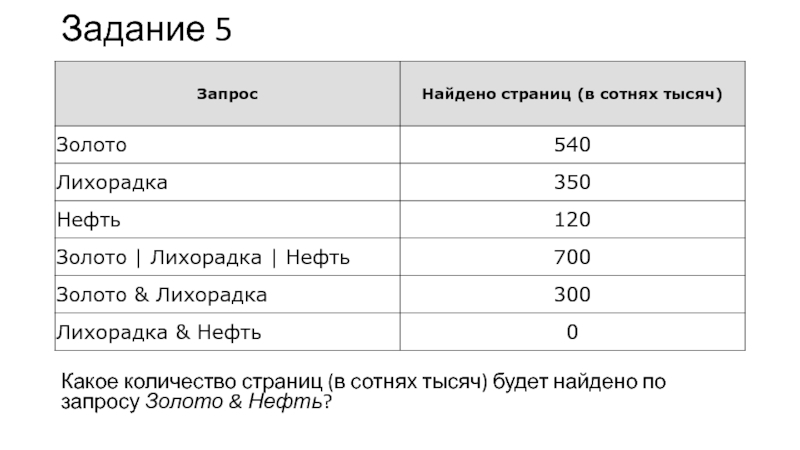
Слайд 12Задание 5
Какое количество страниц (в сотнях тысяч) будет найдено
по запросу Золото & Нефть?
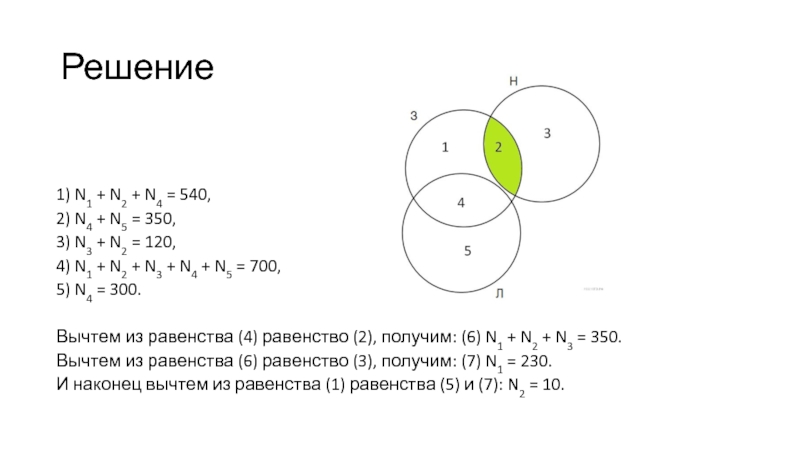
Слайд 13Решение
1) N1 + N2 + N4 = 540,
2) N4 + N5 = 350,
3) N3 + N2 =
120,
4) N1 + N2 + N3 + N4 + N5 = 700,
5) N4 = 300.
Вычтем из
равенства (4) равенство (2), получим: (6) N1 + N2 + N3 = 350.
Вычтем из равенства (6) равенство (3), получим: (7) N1 = 230.
И наконец вычтем из равенства (1) равенства (5) и (7): N2 = 10.
Слайд 15Решение
Англия & Уэльс & Шотландия | Англия & Ирландия =
450
Англия & Уэльс & Шотландия
Англия & Уэльс & Шотландия &
Ирландия
NB = N(A|B) − NA + N(A&B) = 450 – 213 + 87 = 324
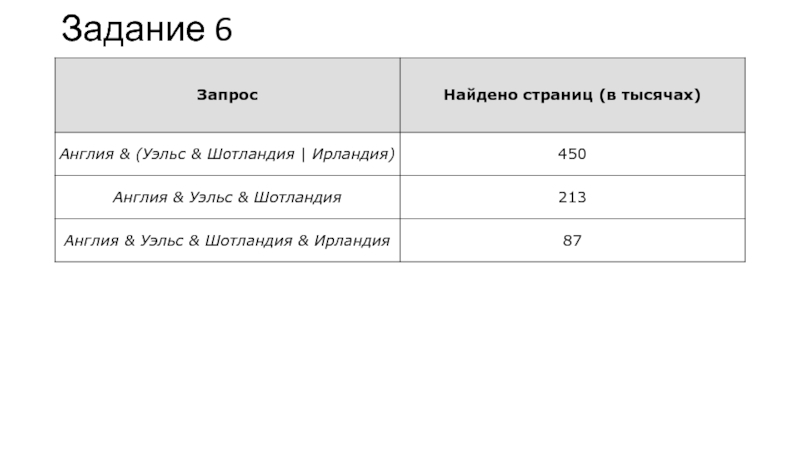
Слайд 16Задание 7
Ниже приведены запросы к поисковому серверу. Расположите номера запросов
в порядке убывания количества страниц, которые найдет поисковый сервер по
каждому запросу.
1) спорт & футбол & чемпионат
2) спорт | футбол & чемпионат
3) cпорт | футбол | чемпионат & 2006
4) спорт | футбол | чемпионат
Слайд 18Задание 8
В языке запросов поисковой системы кавычки вокруг части
запроса означают, что эта часть должна встречаться точно в указанной
форме (т. е. это цитата). Ниже приведены поисковые запросы, одновременно выданные к одной поисковой системе. Расположите их в порядке возрастания количества найденных документов:
1) Откуда берется мокрый снег
2) «Откуда берется мокрый снег»
3) Мокрый&снег&(откуда берется)
4) Мокрый&снег
Слайд 19Решение
Логическая операция “И” истинна только тогда, когда истинны оба аргумента.
Например, чтобы было истинно «канарейки & содержание» необходимо, чтобы в
тексте содержалось и слово «канарейки» и слово «содержание».
Для истинности логической операции “ИЛИ” достаточно истинности лишь одного из ее аргументов. Например, чтобы было истинно «канарейки ∨ содержание» необходимо, чтобы в тексте содержалось или слово «канарейки» или слово «содержание». Вывод: чем больше «&», тем меньшее количество страниц найдет поисковик, чем больше «|», тем большее.
На запрос 1 будет найдено больше документов, чем на запрос 2, так как запрос 2 требует расположения слов точно в указанной форме, то есть порядок слов тоже должен сохраняться, следовательно, по второму запросу будет найдено наименьшее количество страниц. По запросу 3 будет найдено меньше документов чем по запросу 4.
Ответ: 2341.
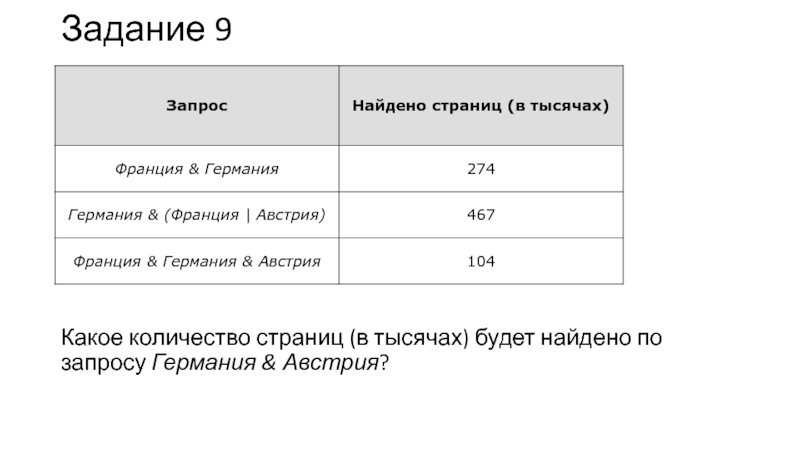
Слайд 20Задание 9
Какое количество страниц (в тысячах) будет найдено по
запросу Германия & Австрия?
Слайд 21Решение
Нарисуем диаграмму Венна для этой задачи.
Тогда по условию дано:
1) S6
+ S7 = 274
2) S4 + S6 + S7 =
467
3) S7 = 104
Нужно найти S4 + S7.
Вычтем третье равенство из первого.
Получим 4) S6 = 170.
Теперь из второго вычтем четвёртое.
Получим S4 + S7 = 297.
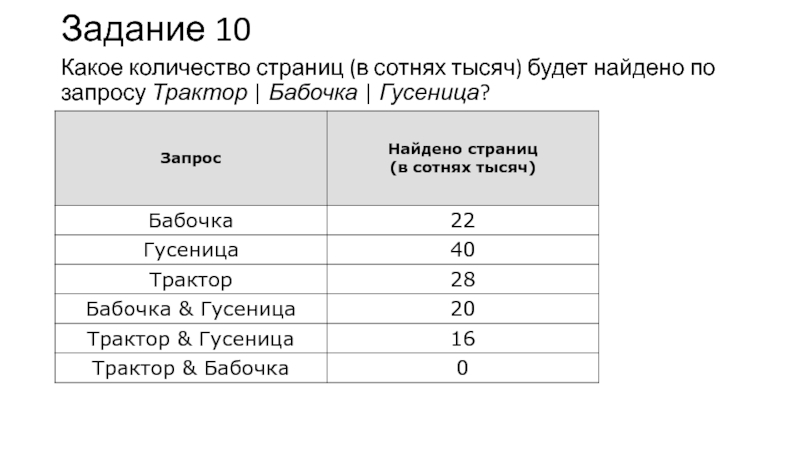
Слайд 22Задание 10
Какое количество страниц (в сотнях тысяч) будет найдено
по запросу Трактор | Бабочка | Гусеница?
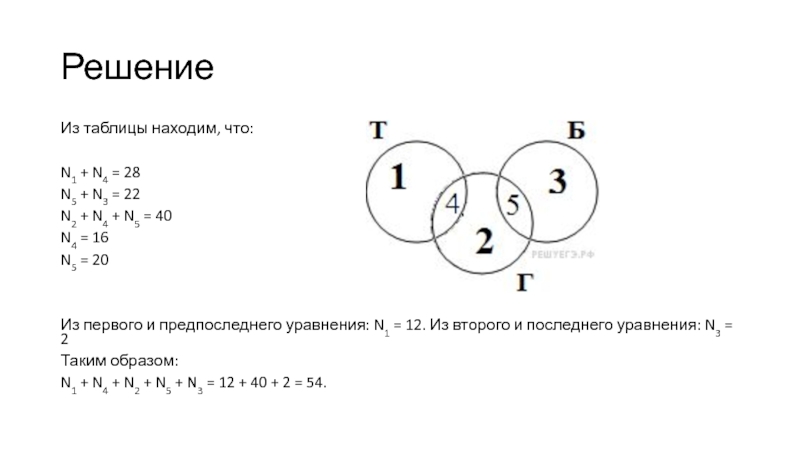
Слайд 23Решение
Из таблицы находим, что:
N1 + N4 = 28
N5 + N3 = 22
N2 + N4 + N5 =
40
N4 = 16
N5 = 20
Из первого и предпоследнего уравнения: N1 = 12. Из
второго и последнего уравнения: N3 = 2
Таким образом:
N1 + N4 + N2 + N5 + N3 = 12 + 40 + 2 = 54.
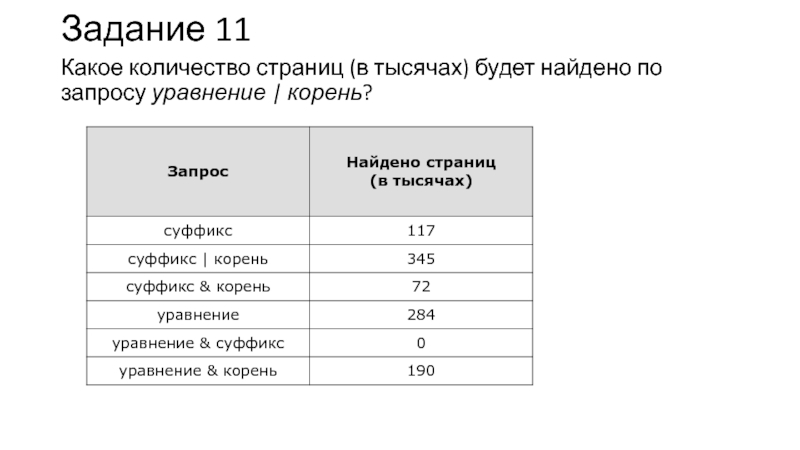
Слайд 24Задание 11
Какое количество страниц (в тысячах) будет найдено по
запросу уравнение | корень?
Слайд 25Решение
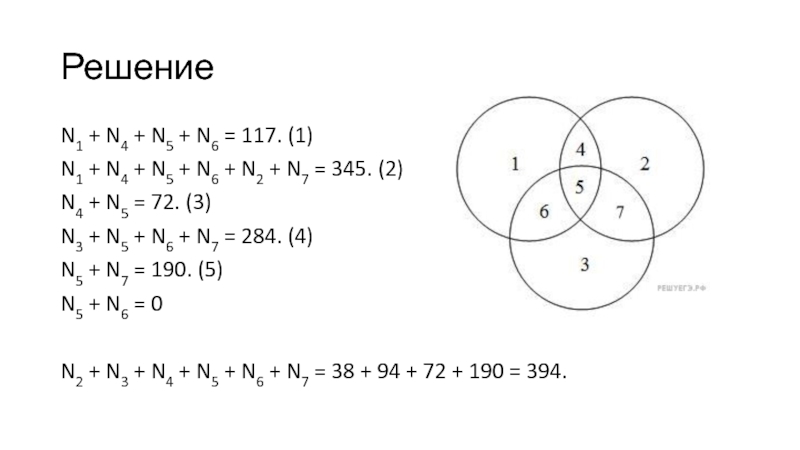
N1 + N4 + N5 + N6 = 117. (1)
N1 + N4 + N5 + N6 + N2 +
N7 = 345. (2)
N4 + N5 = 72. (3)
N3 + N5 + N6 + N7 = 284.
(4)
N5 + N7 = 190. (5)
N5 + N6 = 0
N2 + N3 + N4 + N5 + N6 + N7 = 38 + 94 + 72 + 190 = 394.
Слайд 26Логические высказывания
Задание B18
Слайд 27Задание 1
На числовой прямой даны два отрезка: P = [17, 46]
и Q = [22, 57]. Отрезок A таков, что приведённая ниже формула истинна при
любом значении переменной х:
¬(x ∈ A) →(((x ∈ P) ⋀ (x ∈ Q)) → (x ∈ A))
Какова наименьшая возможная длина отрезка A?
Слайд 28Решение
1) A ∨ (¬(P · Q) ∨ A)
2) ¬P ∨
¬Q ∨ A
A должно быть истинно как минимум на отрезке
[22; 46]. Длина отрезка равна 46 − 22 = 24.
Слайд 29Задание 2
Сколько существует целых значений числа A, при которых формула
((x
6) → (x2
любых целых неотрицательных x и y?










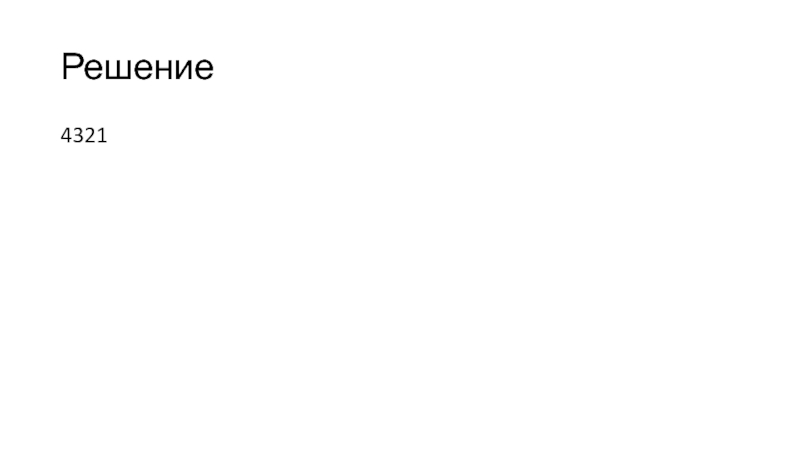




![Занятие №10 Задание 1 На числовой прямой даны два отрезка: P = [17, 46] и Q = Задание 1 На числовой прямой даны два отрезка: P = [17, 46] и Q = [22, 57]. Отрезок A таков, что приведённая ниже](/img/thumbs/44038ec960035d5ab5766170b6cdd39a-800x.jpg)