Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Предел числовой последовательности. Теоремы о пределах. Бесконечно малые и бесконечно большие последовательности
Содержание
- 1. Предел числовой последовательности. Теоремы о пределах. Бесконечно малые и бесконечно большие последовательности
- 2. Математика может открыть определенную последовательность даже в хаосе. Гертруда Стайн (1874 – 1946г.)
- 3. Понятие предела на интуитивном уровне использовалось ещё
- 4. Метод заключался в следующем: для нахождения площади
- 5. Наиболее плодотворным метод исчерпывания стал в руках
- 6. площадь поверхности сферы равна учетверённой площади большого
- 7. Понятие предела на интуитивном уровне использовалось ещё
- 8. Эволюция понятие предела происходила на протяжении 2500
- 9. Число b называется пределом последовательности (bn) ,
- 10. Многих художников привлекали пластические возможности понятий предела
- 11. Предел круга III
- 12. Математика может открыть определенную последовательность даже в хаосе. Гертруда Стайн (1874 – 1946г.)
- 13. Эта последовательность длин диаметров дает пример переменной
- 14. С рассмотренной последовательностью вписанных окружностей свяжем другую
- 15. Теоремы о пределах1.2.3.4.5.6.,где, (bn ) где
- 16. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Математика может открыть определенную последовательность
даже в хаосе.
Гертруда Стайн
(1874 – 1946г.)
Слайд 3Понятие предела на интуитивном уровне использовалось ещё
в глубокой
древность, связано оно с исследованием площадей
фигур и объёмов тел.
Идея предельных переходов была использована величайшим греческим математиком IV в. до н.э.
Евдоксом Книдским( метод исчерпывания).
Евдокс Книдский
IV в. до н.э.
Слайд 4Метод заключался в следующем: для нахождения площади (или объёма) некоторой
фигуры в эту фигуру вписывалась монотонная последовательность других фигур и
доказывалось, что их площади (объёмы) неограниченно приближаются к площади (объёму) искомой фигуры. Затем вычислялся предел последовательности площадей (объёмов), для чего выдвигалась гипотеза, что он равен некоторому A и доказывалось, что обратное приводит к противоречию. Поскольку общей теории пределов не было (греки избегали понятия бесконечности), все эти шаги, включая обоснование единственности предела, повторялись для каждой задачи. С помощью метода исчерпывания Евдокс нашёл площадь круга, объём пирамиды и конуса.метод исчерпывания
Слайд 5Наиболее плодотворным метод исчерпывания стал в руках выдающегося последователя Евдокса,
Архимеда(287 до н. э. — 212 до н. э). который
смог его значительно усовершенствовать и виртуозно применял для многих новых открытий.Архимед
(287 до н. э. — 212 до н. э)
Слайд 6площадь поверхности сферы равна учетверённой площади большого круга этой сферы;
В
частности, он обнаружил, что объём шара составляет 2/3 объёма описанного
вокруг него цилиндра.Открытия Архимеда
Слайд 7Понятие предела на интуитивном уровне использовалось ещё во второй половине
17 века английским физиком, математиком и астрономом Исааком Ньютоном (1642
- 1727), а также математиками 18 века - швейцарским, немецким и русским математиком Леонардом Эйлером (1707 - 1783) и французским математиком, астрономом и механиком Жозефом Луи Лагранжем (1736 - 1813). Это было связано с тем, что ученые того времени не ставили перед собой задачу построения теории пределов.Исаак Ньютон
(1642 – 1727)
Леонард Эйлер
(1707 - 1783)
ЖозефЛуи Лагранж
(1736 – 1813)
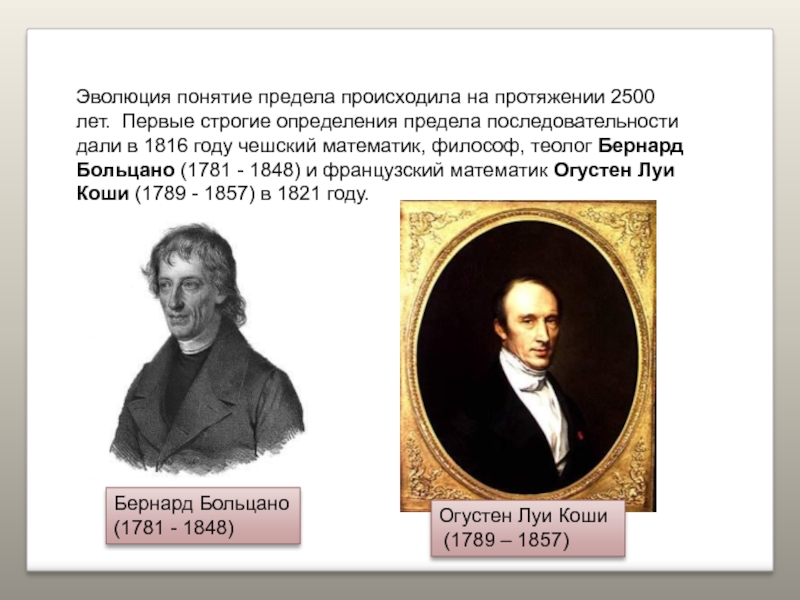
Слайд 8Эволюция понятие предела происходила на протяжении 2500 лет. Первые строгие
определения предела последовательности дали в 1816 году чешский математик, философ,
теолог Бернард Больцано (1781 - 1848) и французский математик Огустен Луи Коши (1789 - 1857) в 1821 году.Бернард Больцано
(1781 - 1848)
Огустен Луи Коши
(1789 – 1857)
Слайд 9
Число b называется пределом последовательности (bn) , если для любого
положительного числа найдётся такое натуральное число N,
что при всех n>N выполняется неравенство :Геометрически это значит, что для любого ε > 0 можно найти такое число N, что начиная с n > N все члены последовательности расположены внутри интервала (b – ε, b + ε).
b
b+
b-
b2
b1
b3
b4
b5
b6
Слайд 10Многих художников привлекали пластические возможности понятий предела и бесконечности. На
иллюстрации — одна из работ голландского художника Маурица Корнелиса Эшера
(1898—1972), вдохновленного этой темой.В современной математике предел является одним из самых загадочных понятий.
Мир бабочек
Слайд 12Математика может открыть определенную последовательность
даже в хаосе.
Гертруда Стайн
(1874 – 1946г.)
Слайд 13
Эта последовательность длин диаметров дает пример переменной величины x n
, которая в процессе своего изменения, т. е.
с возрастанием номера
n , неограниченно приближается к нулю. Предел этой последовательности равен нулю:Предел - важнейшее понятие математики.
Последовательность вписанных
все уменьшающихся окружностей
и соответствующую им последовательность длин их диаметров: x1, x2, x3,x4,… .
Слайд 14
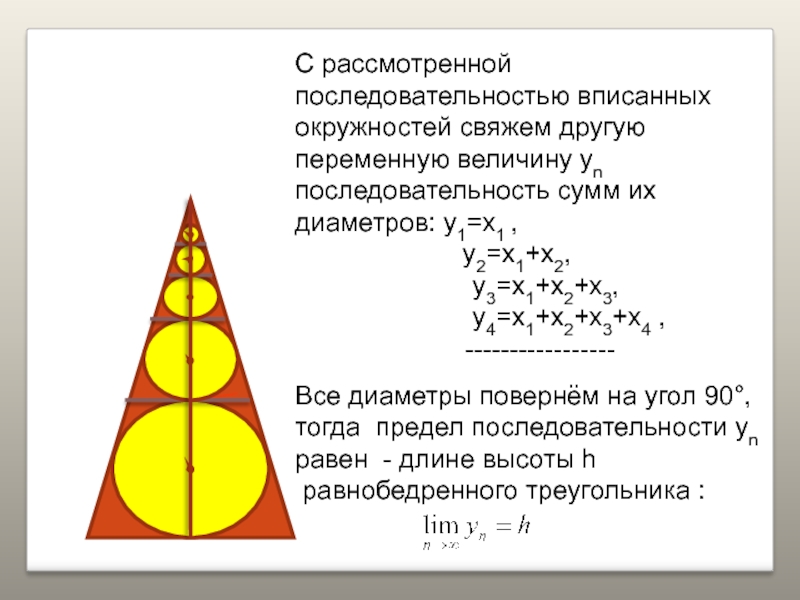
С рассмотренной последовательностью вписанных окружностей свяжем другую переменную величину yn
последовательность сумм их диаметров: y1=x1 ,
y2=x1+x2,y3=x1+x2+x3,
y4=x1+x2+x3+x4 ,
-----------------
Все диаметры повернём на угол 90°,
тогда предел последовательности yn
равен - длине высоты h
равнобедренного треугольника :