Рациональные числа

Содержание

1. Рациональные числа
2. Рациональное число (лат. ratio
3. Множество рациональных
4. Рациональные числа как бесконечные десятичные дробиДля всех
5. Пример. Записать в виде обыкновенной дроби бесконечную
6. Положим х=1,5(23)=1,52323…Сначала умножим на 10. Получим 15,2323..,
7. Замечание: В примере мы видим, что 0,1(9)=0,2(0).
8. Вариант 11. Записать в виде
9. Проверь себяВариант 11. Записать в виде
10. Спасибо за внимание
11. Скачать презентанцию

Рациональное число (лат. ratio — отношение, деление, дробь) — число, представляемое обыкновенной дробью , где числитель m — целое число, а знаменатель n — натуральное число. Такую дробь

Слайды и текст этой презентации

Слайд 1Рациональные числа
Создала: учитель математики МОУ СОШ №19
Короленко Н.И.

Слайд 2
Рациональное число (лат. ratio — отношение, деление,

дробь) — число, представляемое обыкновенной дробью , где числитель m

— целое число, а знаменатель n — натуральное число. Такую дробь следует понимать как результат деления m на n, даже если нацело разделить не удаётся. В реальной жизни рациональные числа используются для счёта частей некоторых целых, но делимых объектов, например, тортов или других продуктов, разрезаемых на несколько частей

Рациональное число (лат. ratio — отношение, деление, дробь) — число, представляемое обыкновенной дробью ,

Слайд 3
Множество рациональных чисел

Множество

рациональных чисел обозначается и может быть записано в виде:

Нужно понимать, что численно равные дроби

такие как, например, и , входят в это множество как

одно число. Поскольку делением числителя и знаменателя дроби на их наибольший общий делитель можно получить единственное несократимое представление рационального числа, то можно говорить об их множестве как о множестве несократимых дробей со взаимно простыми целым числителем и натуральным знаменателем:

Множество рациональных чисел Множество рациональных чисел обозначается и может быть записано

Слайд 4Рациональные числа как бесконечные десятичные дроби
Для всех рациональных чисел можно

использовать один и тот же способ записи. Рассмотрим
1. Целое число

5
5,000
2. Обыкновенную дробь
0, 3(18)
3. Десятичную дробь 8,377
8,3(7)

Рациональные числа как бесконечные десятичные дробиДля всех рациональных чисел можно использовать один и тот же способ записи.

Слайд 5Пример. Записать в виде обыкновенной дроби бесконечную десятичную периодическую дробь.
Положим,

что х=1,(23), т.е. 1,232323…
100х=123,2323…

100х=123,2323…
х=1,2323…
99х=122

х=

Итак: 1,(23)=

Пример. Записать в виде обыкновенной дроби бесконечную десятичную периодическую дробь.Положим, что х=1,(23), т.е. 1,232323…100х=123,2323… 100х=123,2323…

Слайд 6
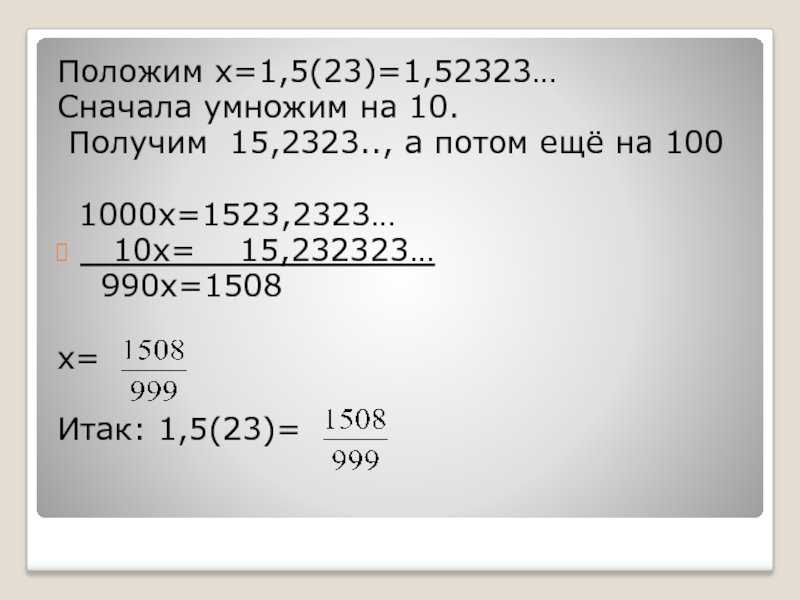
Положим х=1,5(23)=1,52323…
Сначала умножим на 10.
Получим 15,2323.., а потом ещё

на 100

1000х=1523,2323…
10х= 15,232323…
990х=1508

х=

Итак:

1,5(23)=

Слайд 7Замечание: В примере мы видим, что 0,1(9)=0,2(0). Аналогично можно установить,

что 2,45(9)=2,46(0) и т.д. Поэтому обычно десятичные дроби с периодом

9 не рассматриваются, заменяют их соответственно дробями с периодом 0.

Пусть х=0,1(9), тогда
100х=19,999…
-10х= 1,999…
90х=18
Итак, х=0,1(9)= = , но

= 0,2

Замечание: В примере мы видим, что 0,1(9)=0,2(0). Аналогично можно установить, что 2,45(9)=2,46(0) и т.д. Поэтому обычно десятичные

Слайд 8
Вариант 1
1. Записать в виде

а)

б)

2. Представьте

в виде
а) 15,(3)
б) 2,(14)
в) 1,6(1)
Вариант 2
бесконечной дроби

а)

б)

обыкновенной дроби
а) 7,(2)
б)

23,(25)
в) 3,9(12)

Самостоятельная работа

Вариант 11. Записать в виде а)б) 2. Представьте в видеа) 15,(3)б) 2,(14)в) 1,6(1)Вариант 2бесконечной дробиа)

Слайд 9Проверь себя
Вариант 1
1. Записать в виде
а) 0, (05)
б)

4,41(6)
2. Представьте в виде

а)

б)

в)

Вариант 2
бесконечной дроби
а) 0,1(3)
б) 7,(09)
обыкновенной дроби

а)

б)

в)

Проверь себяВариант 11. Записать в виде а) 0, (05)б) 4,41(6)2. Представьте в видеа)б)в)Вариант 2бесконечной дробиа) 0,1(3)б)

Слайд 10Спасибо за внимание

Скачать презентацию

Разделы презентаций

Рациональные числа

Содержание

Слайды и текст этой презентации

Слайд 1Рациональные числа
Создала: учитель математики МОУ СОШ №19
Короленко Н.И.

Слайд 2
Рациональное число (лат. ratio — отношение, деление,

дробь) — число, представляемое обыкновенной дробью , где числитель m

Слайд 3
Множество рациональных чисел

Множество

рациональных чисел обозначается и может быть записано в виде:

Слайд 4Рациональные числа как бесконечные десятичные дроби
Для всех рациональных чисел можно

использовать один и тот же способ записи. Рассмотрим
1. Целое число

Слайд 5Пример. Записать в виде обыкновенной дроби бесконечную десятичную периодическую дробь.
Положим,

что х=1,(23), т.е. 1,232323…
100х=123,2323…

100х=123,2323…
х=1,2323…
99х=122

Слайд 6
Положим х=1,5(23)=1,52323…
Сначала умножим на 10.
Получим 15,2323.., а потом ещё

на 100

1000х=1523,2323…
10х= 15,232323…
990х=1508

х=

Итак:

Слайд 7Замечание: В примере мы видим, что 0,1(9)=0,2(0). Аналогично можно установить,

что 2,45(9)=2,46(0) и т.д. Поэтому обычно десятичные дроби с периодом

Слайд 8
Вариант 1
1. Записать в виде

а)

б)

2. Представьте

в виде
а) 15,(3)
б) 2,(14)
в) 1,6(1)
Вариант 2
бесконечной дроби

а)

б)

обыкновенной дроби
а) 7,(2)
б)

Слайд 9Проверь себя
Вариант 1
1. Записать в виде
а) 0, (05)
б)

4,41(6)
2. Представьте в виде

а)

б)

в)

Вариант 2
бесконечной дроби
а) 0,1(3)
б) 7,(09)
обыкновенной дроби

а)

б)

в)

Слайд 10Спасибо за внимание

Обратная связь

Что такое TheSlide.ru?

Разделы презентаций

Рациональные числа

Содержание

Слайды и текст этой презентации

Слайд 1Рациональные числаСоздала: учитель математики МОУ СОШ №19Короленко Н.И.

Слайд 2 Рациональное число (лат. ratio — отношение, деление,

дробь) — число, представляемое обыкновенной дробью , где числитель m

Слайд 3 Множество рациональных чисел Множество

рациональных чисел обозначается и может быть записано в виде:

Слайд 4Рациональные числа как бесконечные десятичные дробиДля всех рациональных чисел можно

использовать один и тот же способ записи. Рассмотрим1. Целое число

Слайд 5Пример. Записать в виде обыкновенной дроби бесконечную десятичную периодическую дробь.Положим,

что х=1,(23), т.е. 1,232323…100х=123,2323… 100х=123,2323… х=1,2323… 99х=122

Слайд 6Положим х=1,5(23)=1,52323…Сначала умножим на 10. Получим 15,2323.., а потом ещё

на 100 1000х=1523,2323… 10х= 15,232323… 990х=1508х= Итак:

Слайд 7Замечание: В примере мы видим, что 0,1(9)=0,2(0). Аналогично можно установить,

что 2,45(9)=2,46(0) и т.д. Поэтому обычно десятичные дроби с периодом

Слайд 8Вариант 11. Записать в виде а)б) 2. Представьте

в видеа) 15,(3)б) 2,(14)в) 1,6(1)Вариант 2бесконечной дробиа) б)обыкновенной дробиа) 7,(2)б)

Слайд 9Проверь себяВариант 11. Записать в виде а) 0, (05)б)

4,41(6)2. Представьте в видеа)б)в)Вариант 2бесконечной дробиа) 0,1(3)б) 7,(09)обыкновенной дробиа) б)в)

Слайд 10Спасибо за внимание

Похожие презентации

Обратная связь

Что такое TheSlide.ru?

Слайд 1Рациональные числа
Создала: учитель математики МОУ СОШ №19
Короленко Н.И.

Слайд 2
Рациональное число (лат. ratio — отношение, деление,

Слайд 3
Множество рациональных чисел

Множество

Слайд 4Рациональные числа как бесконечные десятичные дроби
Для всех рациональных чисел можно

использовать один и тот же способ записи. Рассмотрим
1. Целое число

Слайд 5Пример. Записать в виде обыкновенной дроби бесконечную десятичную периодическую дробь.
Положим,

что х=1,(23), т.е. 1,232323…
100х=123,2323…

100х=123,2323…
х=1,2323…
99х=122

Слайд 6
Положим х=1,5(23)=1,52323…
Сначала умножим на 10.
Получим 15,2323.., а потом ещё

на 100

1000х=1523,2323…
10х= 15,232323…
990х=1508

х=

Итак:

Слайд 8
Вариант 1
1. Записать в виде

а)

б)

2. Представьте

в виде
а) 15,(3)
б) 2,(14)
в) 1,6(1)
Вариант 2
бесконечной дроби

а)

б)

обыкновенной дроби
а) 7,(2)
б)

Слайд 9Проверь себя
Вариант 1
1. Записать в виде
а) 0, (05)
б)

4,41(6)
2. Представьте в виде

а)

б)

в)

Вариант 2
бесконечной дроби
а) 0,1(3)
б) 7,(09)
обыкновенной дроби

а)

б)

в)